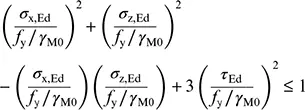c) Außerhalb der Fließgelenkbereiche eines Bauteils müssen die druckbeanspruchten Gurte der Querschnittsklasse 1 oder 2 und die Stege der Querschnittsklasse 1, 2 oder 3 entsprechen.
(4) Angrenzend an ein Fließgelenk müssen die Löcher in zugbeanspruchten Trägerflanschen innerhalb eines Abstands nach (3)b) in jeder Richtung vom Fließgelenk den Anforderungen nach 6.2.5(4) entsprechen.
(5) Falls eine plastische Bemessung eines Rahmens unter Beachtung der Querschnittsanforderungen durchgeführt wird, darf das plastische Umlagerungsvermögen als ausreichend angenommen werden, wenn die Anforderungen nach (2) bis (4) für alle Bauteile, in denen Fließgelenke unter den Bemessungswerten der Einwirkungen auftreten können, erfüllt sind.
(6) Falls eine plastische Tragwerksberechnung durchgeführt wird, welche das tatsächliche Spannungs- und Dehnungsverhalten entlang der Längsachse des Bauteils einschließlich lokalem Beulen und globalem Knicken des Bauteils und des Tragwerks berücksichtigt, ist es nicht erforderlich die Anforderung (2) bis (5) zu erfüllen.
6 Grenzzustände der Tragfähigkeit
6.1 Allgemeines
(1) Die charakteristischen Werte der Beanspruchbarkeit, die in diesem Abschnitt angegeben werden, werden mit den in 2.4.3 definierten Teilsicherheitsbeiwerten γ Mwie folgt abgemindert:
– die Beanspruchbarkeit von Querschnitten (unabhängig von der Querschnittsklasse): γM0
– die Beanspruchbarkeit von Bauteilen bei Stabilitätsversagen (bei Anwendung von Bauteilnachweisen): γM1
– die Beanspruchbarkeit von Querschnitten bei Bruchversagen infolge Zugbeanspruchung: γM2
– die Beanspruchbarkeit von Anschlüssen: siehe EN 1993-1-8
Anmerkung 1: Weitere Empfehlungen für Zahlenwerte sind in EN 1993-2 bis EN 1993-6 zu finden. Teilsicherheitsbeiwerte γ Mifür Tragwerke, die nicht durch EN 1993-2 bis EN 1993-6 erfasst werden, sind im Nationalen Anhang festgelegt; es wird die Verwendung der Teilsicherheitsbeiwerte γ Minach EN 1993-2 empfohlen.
zu 6.1(1) Anmerkung 1
Es gilt die Empfehlung.
Anmerkung 2B: Der Nationale Anhang kann die Teilsicherheitsbeiwerte γ Mifür Hochbauten festlegen.
Folgende Zahlenwerte werden empfohlen:
γ M0= 1,00;
γ M1= 1,00;
γ M2= 1,25.
zu 6.1(1) Anmerkung 2B
Die Teilsicherheitswerte γ Mifür Hochbauten sind wie folgt festgelegt:
– γM0 = 1,0;
– γM1 = 1,1;
– γM2 = 1,25.
Bei Stabilitätsnachweisen in Form von Querschnittsnachweisen mit Schnittgrößen nach Theorie II. Ordnung (siehe 5.2) ist bei der Ermittlung der Beanspruchbarkeit von Querschnitten statt γ M0der Wert γ M1= 1,1 anzusetzen.
Die Teilsicherheitswerte γ Misind für außergewöhnliche Bemessungssituationen wie folgt festgelegt:
– γM0 = 1,0;
– γM1 = 1,0;
– γM2 = 1,15.
6.2 Beanspruchbarkeit von Querschnitten
6.2.1 Allgemeines
(1) P Der Bemessungswert der Beanspruchung darf in keinem Querschnitt den zugehörigen Bemessungswert der Beanspruchbarkeit überschreiten. Falls mehrere Beanspruchungsarten gleichzeitig auftreten, gilt diese Forderung auch für die Kombination dieser Beanspruchungen.
Zu 6.1(1) und NDP zu 6.1(1) Anmerkung 2B
Es werden zwei unterschiedliche Teilsicherheitsbeiwerte definiert: γ M0für die Querschnittsnachweise nach Abs. 6.2 für alle Querschnittsklassen (also auch für beulgefährdete Querschnitte der Klasse 4) und γ M1für Stabilitätsnachweise von Bauteilen nach Abs. 6.3. Diese Unterscheidung war für die ursprüngliche Empfehlung in EN 1993-1-1 unerheblich, weil beide Werte darin zu 1,0 empfohlen wurden. Der deutsche Nationale Anhang ist aber nicht der Empfehlung gefolgt, sondern hat für die beiden Teilsicherheitsbeiwerte unterschiedliche Werte, nämlich γ M0zu 1,0 und γ M1zu 1,1 gewählt, zu den Argumenten siehe [K44]. Wegen der oben erläuterten Differenzierung, die sich mit dem Begriff „Bauteilnachweis“ eigentlich nur auf die Nachweise nach Abs. 6.3 bezieht und theoretisch nicht auf die Querschnittsnachweise mit Schnittgrößen nach Theorie II. Ordnung, wird im Text des NDP klargestellt, dass auch Querschnittsnachweise mit Schnittgrößen nach Theorie II. Ordnung als Stabilitätsnachweise zu verstehen sind und hierfür der erhöhte Teilsicherheitsbeiwert γ M1gilt.
Ähnlich folgt der Nationale Anhang für EN 1993-2 Stahlbrücken auch nicht der Empfehlung bezüglich der Behandlung von beulgefährdeten Querschnitten der Klasse 4, sondern legt fest, dass bei Anwendung von γ M0in EN 1993-1-5 ein Wert von 1,1 anzusetzen ist. Entsprechend verschiedener Quellen, siehe [K44], ist hier dringend zu empfehlen, bei entsprechenden schlanken Klasse-4-Querschnitten anderer Anwendungsbereiche, wie zum Beispiel bei Kranbahnen dem Brückenbau mit γ M0von 1,1 in allen Nachweisen nach EN 1993-1-5 zu folgen.
Zu 6.1(7)
Die Übersetzung „wobei N Rd, M y,Rdund M z,Rddie Bemessungswerte der Tragfähigkeiten in Abhängigkeit von der Querschnittsklasse unter möglicher Berücksichtigung mittragender Breiten sind, siehe 6.2.8.“ ist nicht korrekt. Gemeint ist nach dem englischen Normentext „wobei N Rd, M y,Rdund M z,Rddie Bemessungswerte der Tragfähigkeiten abhängig von der Querschnittsklasse und unter Berücksichtigung des Querkrafteinflusses nach 6.2.8 sind.“
(2) Dabei sind in der Regel die mittragende Breite und die mitwirkende Breite infolge lokalen Beulens nach EN 1993-1-5 zu berücksichtigen. Ferner sollte Schubbeulen nach EN 1993-1-5 betrachtet werden.
(3) Die Bemessungswerte der Beanspruchbarkeit hängen von der Querschnittsklassifizierung ab.
(4) Ein Nachweis nach Elastizitätstheorie entsprechend der elastischen Beanspruchbarkeit ist für alle Querschnittsklassen möglich, sofern für Querschnitte der Klasse 4 die wirksamen Querschnittswerte angesetzt werden.
(5) Für den Nachweis nach Elastizitätstheorie darf das folgende Fließkriterium für den kritischen Punkt eines Querschnitts verwendet werden, wenn nicht andere Interaktionsformeln vorgezogen werden, siehe 6.2.8 bis 6.2.10.
(6.1) 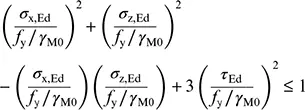
Dabei ist
| σ x,Ed |
der Bemessungswert der einwirkenden Normalspannung in Längsrichtung am betrachteten Punkt; |
| σ z,Ed |
der Bemessungswert der einwirkenden Normalspannung in Querrichtung am betrachteten Punkt; |
| τ Ed |
der Bemessungswert der einwirkenden Schubspannung am betrachteten Punkt. |
Anmerkung: Die Nachweisführung nach (5) kann konservativ sein, da sie die teilweise plastischen Spannungsumlagerungen, welche in der elastischen Bemessung erlaubt sind, nicht berücksichtigt. Deshalb sollte sie nur angewendet werden, wenn die Interaktion auf der Grundlage der Beanspruchbarkeitswerte N Rd, M Rd, V Rdnicht verwendbar ist.
(6) Die plastische Querschnittstragfähigkeit ist in der Regel durch eine zu den plastischen Verformungen passende Spannungsverteilung zu bestimmen, die mit den inneren Kräften im Gleichgewicht steht, ohne dass die Streckgrenze überschritten wird.
(7) Als konservative Näherung darf für alle Querschnittsklassen eine lineare Addition der Ausnutzungsgrade für alle Schnittgrößen angewendet werden. Für Querschnitte der Klasse 1, 2 und 3, die durch eine Kombination von N Ed, M y,Edund M z,Edbeansprucht werden, führt diese Regelung zu folgendem Kriterium:
Читать дальше