Rafael Riddell Carvajal - Fundamentos de ingeniería estructural para estudiantes de arquitectura

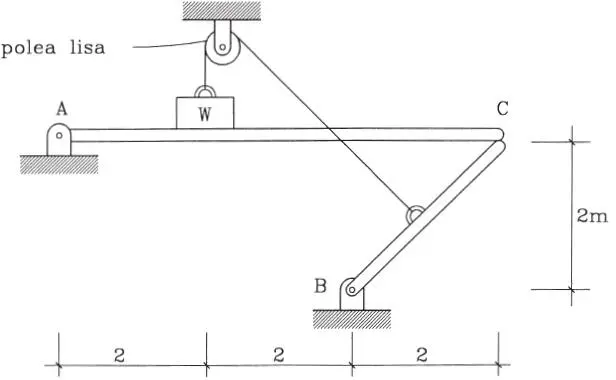
1.50 La barra uniforme AB de la figura pesa 40 kg y puede girar libremente en torno a la articulación en B. El hombre pesa 80 kg y tira de la cuerda que sostiene la barra. La cuerda pasa por un semicilindro fijo con coeficiente de roce 0,4. Calcular la fuerza mínima vertical que debe hacer el hombre para mantener el equilibrio. (Respuesta: 31,91 kg)

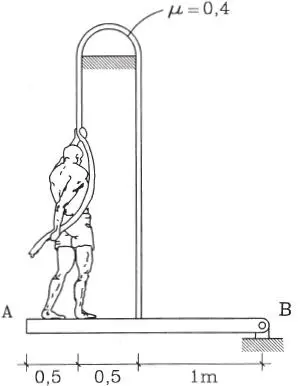
1.51 La barra AB de la figura “a” tiene peso W, largo L, y está articulada en el punto B. El extremo A se sostiene mediante un hilo liviano, que pasa por una polea lisa, del cual cuelga un bloque en su otro extremo. Se pide: a) Determinar cuánto debe pesar el bloque para que la barra AB esté en equilibrio, b) Suponiendo que el bloque tiene efectivamente el valor antes calculado, pero en vez de estar la barra articulada en B sólo se apoya en un plano rugoso con coeficiente μ=0,7 como muestra la figura “b”. ¿Está la barra en equilibrio?. (Respuesta: a) 0,765W; b) No, porque la reacción horizontal necesaria para el equilibrio 0,382W excede la máxima fuerza de fricción que puede desarrollarse en el contacto 0,236W)

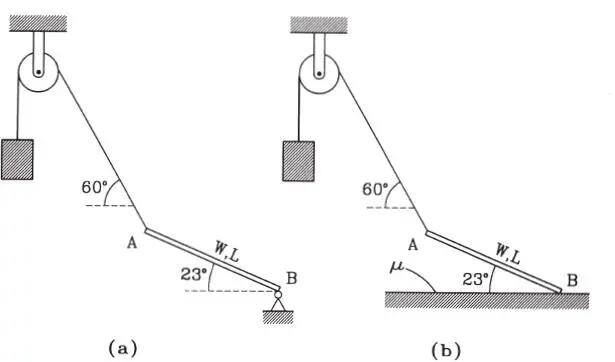
1.52 Una viga homogénea que pesa 1000 kg, tiene 3 m de longitud, es paralela a un plano vertical, y se apoya de las distintas maneras indicadas. Los rodillos y las poleas son lisos; en los otros contactos hay roce con los coeficientes de fricción indicados. Se pide: a) en la figura “a” calcular las reacciones en los apoyos; b) en la figura “b”, ¿está la viga en equilibrio?; c) en la figura “c”, determinar el máximo valor de P compatible con el equilibrio. (Respuesta: a) normal a la barra en A 532,6 kg, tangencial 221,9 kg, vertical en B 423 kg; b) No; c) normal a la barra en A 532,5 kg, vertical en B 508,5 kg, P max=459,3 kg)

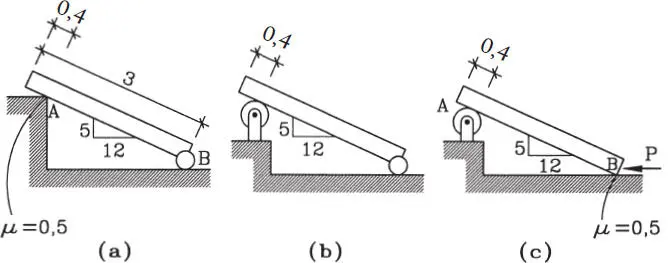
1.53 Un hombre de peso W ha colocado una escalera sin peso de longitud L con la pendiente indicada y empezado a ascender por ella. Si los coeficientes de fricción entre la escalera y el piso y entre la escalera y la pared son ambos de 0,25, encuentre cuánto puede subir el hombre (distancia x en la figura) antes de que la escalera resbale. Compruebe y explique por qué antes de ocurrir la condición límite de equilibrio por deslizamiento no es posible encontrar las reacciones del piso y la pared. (Respuesta: x=0,376L; hay 4 incógnitas y sólo 3 ecuaciones, es decir, es un problema hiperestático).

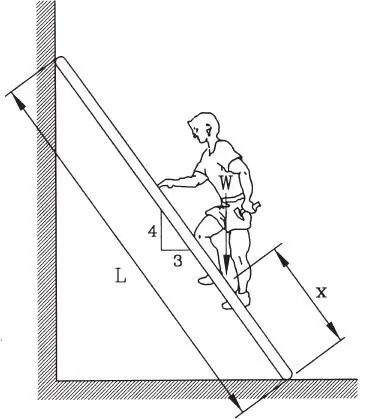
1.54 La barra de la figura está sostenida por una articulación en B y por un cable en A. Encuentre: a) la tensión en el cable, b) las reacciones en B. (Respuesta: a) 2588, b) V=2157, H=2315)

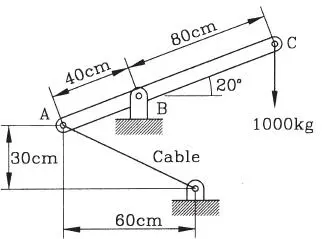
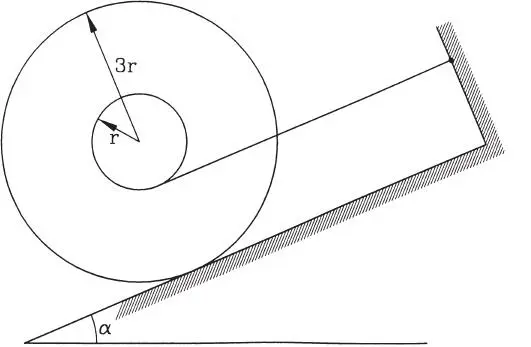
1.55 Una rueda de radio 3r y peso W se encuentra sobre un plano inclinado rugoso y está sujeta por una cuerda enrollada a su eje de radio r (la cuerda de varias vueltas sobre el eje de modo que no puede deslizar sobre él), a) Si la rueda está en equilibrio, determinar la reacción del plano sobre ella y la tensión en la cuerda, b) Determinar el coeficiente de fricción mínimo requerido para que sea posible el equilibrio. (Respuesta: a) N=Wcosα, F r=0,5Wsenα, T=3F r; b) μ=0,5tgα)

II.

ANÁLISIS DE ESTRUCTURAS ISOSTÁTICAS

2.1 Equilibrio Global

2.1.1 Grados de Libertad y Vinculación

En muchos de los sistemas estudiados en el Capítulo anterior el equilibrio se lograba sólo para valores muy precisos de algunas fuerzas o para configuraciones geométricas específicas. Ello porque en su mayoría dichos sistemas estaban constituidos por cuerpos y superficies en condiciones de simple contacto, que pueden desbaratarse si se les somete a sistemas de fuerzas distintos. Por ejemplo, el sistema de la Fig. 1.32 dejaría de funcionar si sobre la barra AB se aplicara una fuerza que la hiciera levantarse de su apoyo en A.

Las estructuras en cambio, en general, tienen la cualidad de ser fijas , esto es, no pueden moverse cualesquiera sea el sistema de fuerzas que se les aplique. Como se recordará, en la Sección 1.3.2 se mencionaron diversos tipos de cargas que deben soportar las estructuras, entre otros: peso propio, cargas de uso, viento, nieve, sismo, y cambio de temperatura. En contraposición, se llamarán mecanismos los sistemas que tienen la posibilidad de adoptar distintas posiciones dependiendo de las cargas a que estén sometidos.

Al hablar de posibilidades de movimiento se entra al campo de la cinemática , que es la parte de la mecánica que estudia las características geométricas del movimiento sin relacionarlo con las causas que lo producen. La consideración de tales causas es naturalmente el campo de la dinámica.

El aspecto de la cinemática que interesa aquí son los grados de libertad de un sistema, los que se definen como las posibilidades de movimiento del sistema y que en número coinciden con el número de coordenadas necesarias para definir su posición en el espacio. Los tres conceptos mencionados están tan relacionados que prácticamente se confunden: la libertad se expresa en movimiento y éste, que corresponde a cambio de posición , se describe mediante coordenadas.

Un ejemplo sencillo es el de una partícula en el espacio. Sus posibilidades de movimiento son 3: puede desplazarse en dirección norte-sur (cambiar de latitud), en dirección este-oeste (cambiar de longitud), y en dirección vertical (cambiar de cota). Por cierto que de un punto a otro puede desplazarse en una trayectoria cualquiera que los una, pero ese desplazamiento siempre puede expresarse como un cambio de sus tres coordenadas: latitud, longitud, y cota. En vez de usar coordenadas geográficas, podría interesar la posición de la partícula al interior de una sala de clases; en tal caso como coordenadas de referencia puede escogerse un sistema de ejes x, y, z coincidente con un vértice y tres aristas de la sala (Fig. 2.1.a). La posición de la partícula P queda dada por sus coordenadas x p, y py z py sus posibilidades de movimiento son tres: cambiar de posición según x, según y, y según z. Se concluye que una partícula en el espacio tiene 3 grados de libertad.

La restricción de la libertad de movimiento se llama vinculación , la que se especifica imponiendo un vínculo. La vinculación puede ser de muy variada naturaleza, y los vínculos pueden materializarse mediante dispositivos físicos reales como se usarán en las estructuras reales, o simplemente mediante condiciones abstractas. Volviendo al ejemplo de la partícula en la sala de clases, supóngase ahora que se le impone la restricción de mantenerse sobre la pared definida por el plano yz en la Fig. 2.1.a. El establecimiento de un vínculo implica una pérdida de libertad, en efecto, el vínculo establece que x p≡0 y la partícula ahora sólo puede cambiar sus coordenadas y py z p. Se concluye que la partícula en el plano tiene 2 grados de libertad. Es decir el vínculo impuesto le quitó un grado de libertad de los 3 que originalmente tenía en el espacio. En este caso el vínculo es de tipo abstracto, porque no se está detallando como se logra efectivamente que la partícula no abandone el plano. El lector puede imaginar formas físicas de hacerlo.