Rafael Riddell Carvajal - Fundamentos de ingeniería estructural para estudiantes de arquitectura

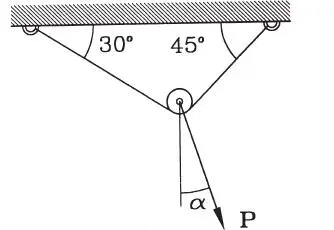
1.20 Un cuerpo que pesa 1000 kg cuelga del sistema de cables flexibles y livianos representados en la figura. Determinar las fuerzas en los cables AC, BC, CD y DE. (Respuesta: T AC=597,72 kg, T BC=1154,70 kg, T CD=1154,70 kg, T DE=577,35 kg)

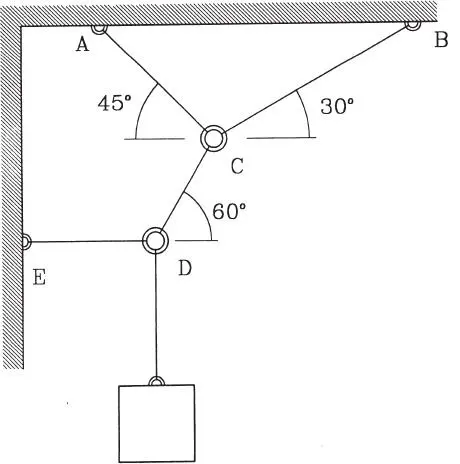
1.21 El polipasto de la figura soporta un peso de 150 kg. Sabiendo que β=20º, hallar la magnitud y la dirección α de la fuerza P que debe ejercerse en el extremo libre de la cuerda para mantener el equilibrio. (Respuesta: 57,5; 46,84º)

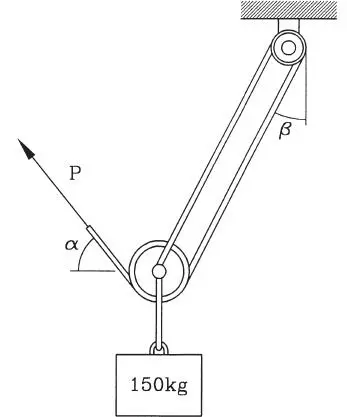
1.22 Un cilindro de peso 15 kg y radio 20 cm descansa sobre otro cilindro de peso 20 kg y radio 30 cm como se muestra. Calcule todas las fuerzas que actúan sobre el cilindro inferior. (Respuesta: 25 kg, 23,45 kg y 23,1 kg)

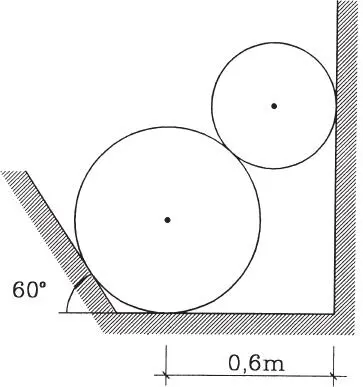
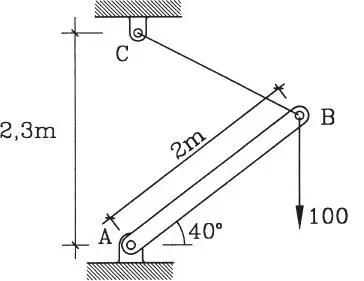
1.23 La barra AB y el hilo BC de la figura no tienen peso. Del punto B se cuelga un peso de 100 kg. Calcular los esfuerzos en la barra y el hilo. (Respuesta: -87; 79,9)

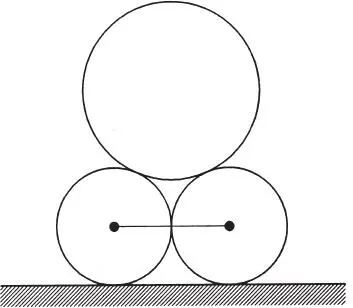
1.24 Dos discos de radio 6 cm y peso P se amarran de sus centros por medio de un hilo sin peso y sostienen sobre ellos a un tercer disco de radio 9 cm y peso 2P. El largo del hilo es tal que la fuerza de contacto entre los discos inferiores es nula. Todos los contactos son lisos. Determine: a) la fuerza que soporta el hilo, b) la reacción del suelo sobre cada uno de los discos inferiores, c) la fuerza de interacción entre un disco inferior y el superior. (Respuesta: T=0,436P, N=2P, R=1,09P)

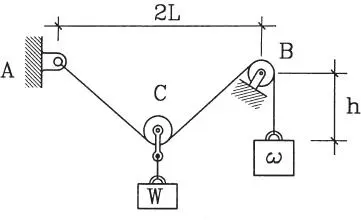
1.25 El cable liviano del sistema de la figura tiene una longitud a. Uno de sus extremos está amarrado a un apoyo fijo en A y el otro a un peso ω después de pasar por una polea lisa en B. Sobre el cable se mueve libremente la rueda C que sostiene el peso W. Demuestre que en la posición de equilibrio Demuestre que sólo hay equilibrio si ω>W/2.

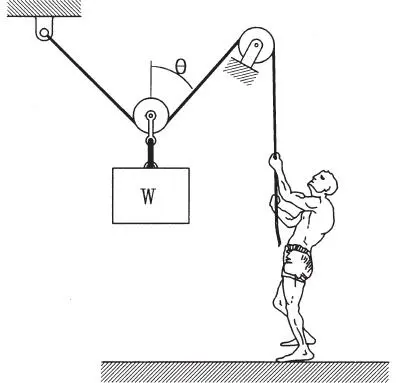
1.26 Un hombre que pesa 80 kg tira en dirección vertical de una cuerda liviana con el objeto de levantar un bloque de peso 25 kg. Calcule la Fuerza F que hace el hombre y grafíquela en función del ángulo θ. Comente las características del gráfico. ¿Cuál es el valor de la fuerza T oen la cuerda y el ángulo θ ocuando el hombre no puede seguir levantando el peso? (Respuesta: T=12,5/cosθ, T o=80, θ o=81°)

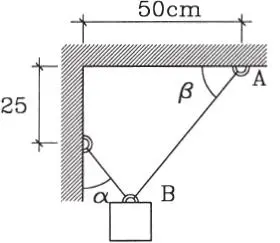
1.27 Un bloque que pesa 10 kg se suspende de una pared y del cielo mediante una cuerda liviana de 80 cm de largo. El gancho puede deslizar libremente sobre la cuerda. Determinar el esfuerzo en la cuerda y los ángulos α y β. (Respuesta: 6,4 kg, α=38,68º, β=51,32º)

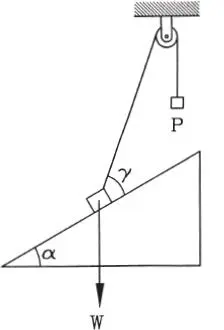
1.28 Un peso W se encuentra descansando sobre un plano liso inclinado en α=30° con la horizontal, atado a una cuerda que pasa sobre la polea lisa A y sostiene en su otro extremo un peso P=0,7W. ¿Qué ángulo γ forma la cuerda con el plano en la posición de equilibrio?. Demostrar que el problema sólo tiene solución si P ≥ 0,5W. (Respuesta: γ =44,41 o)

1.29 Un cilindro de peso 100 y un bloque de peso 200 descansan sobre dos planos inclinados como se muestra. Todos los contactos son lisos. Calcular todas las reacciones externas e internas. (Respuesta: N 1=173, N 2=0, N 3=173, R=100)

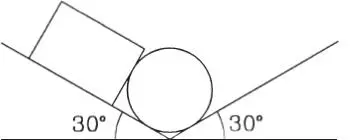
1.30 Dos cilindros lisos de pesos W 1y W 2descansan en contacto dentro del espacio formado por dos planos inclinados en α y β con respecto al plano horizontal. Encontrar las reacciones de los planos sobre los cilindros y la fuerza interna de contacto entre ambos cilindros. (Respuesta: R 1=(W 1+W 2)senβ/sen(α+β), R 2=(W 1+W 2)senα/sen(α + β), tanγ=(W 2cotα–W 1cotβ)/(W 1+W 2), F=R 2senβ/cosγ)

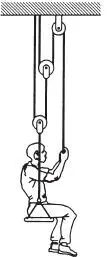
1.31 Determinar la fuerza que debe ejercer sobre la cuerda un hombre de peso W para sostenerse a sí mismo. Determinar la fuerza total que se traspasa al techo. Despreciar el peso de la silla, cuerdas y poleas. (Respuesta: W/5, W)

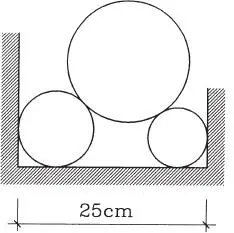
1.32 Tres cilindros de diámetros 8, 10 y 16 cm pesan 222, 350 y 890 kg respectivamente. Determinar las fuerzas que ejercen las paredes y el piso sobre los cilindros inferiores y las fuerzas de interacción entre éstos y el cilindro superior. Todas las superficies lisas. Se sugiere determinar primero los ángulos del triángulo cuyos vértices son los centros de los cilindros. (Respuesta: Ángulos: 47,43º; 52,92º; 79,65º; Reacciones: V 1=696, V 2=766, H=361, R 1=500, R 2=653 kg)

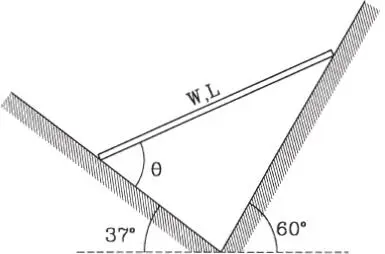
1.33 Determine el ángulo θ para el cual la barra de peso W y largo L estará en equilibrio si los contactos son ambos lisos. Determinar las reacciones de los planos sobre la barra. En ambos casos trate la barra como partícula. (Respuesta: θ=57,55º, 0,606W, 0,873W)

1.34 Los tres bloques de la figura pesan W1=200 kg, W2=100 kg y W3=150 kg. Los coeficientes de fricción en los contactos son los indicados. Determinar la fuerza F que rompe el equilibrio del sistema. (Respuesta: 60 kg)