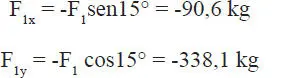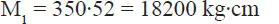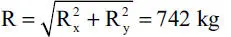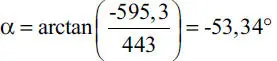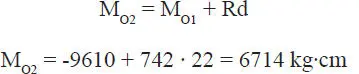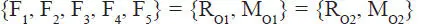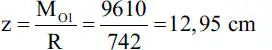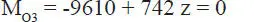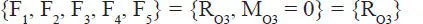Rafael Riddell Carvajal - Fundamentos de ingeniería estructural para estudiantes de arquitectura

Ejemplo 1.18

El sistema de fuerzas de la Figura E1.18.a, referido a los ejes x e y, corresponde a todas las fuerzas (acciones y reacciones) que actúan sobre un cuerpo plano. Se pide: a) reducir el sistema de fuerzas dado a una fuerza y un momento en el punto O 1; b) transformar el sistema anterior en uno estáticamente equivalente a él pero con la fuerza pasando por el punto O 2; c) ¿existe una línea de acción de la fuerza tal que el momento del sistema pueda anularse?; d) ¿está el cuerpo en equilibrio?.

Solución:

a) La traslación paralela de todas las fuerzas al punto O 1corresponde a tener un sistema de fuerzas concurrentes en dicho punto. La resultante (suma) de este sistema de fuerzas se obtendrá haciendo la suma de las componentes horizontales y verticales, y posteriormente componiendo éstas para hallar la resultante R. En particular la fuerza F 1se puede descomponer en

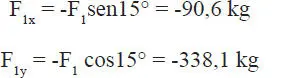
y la distancia de F 1al punto O 1es d 1=52 cm, de manera que el momento de F 1con respecto al punto O 1es

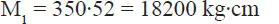
tomándose como positivo los momentos contra los punteros del reloj. Procediendo de igual forma para cada una de las fuerzas, se construye la siguiente tabla:

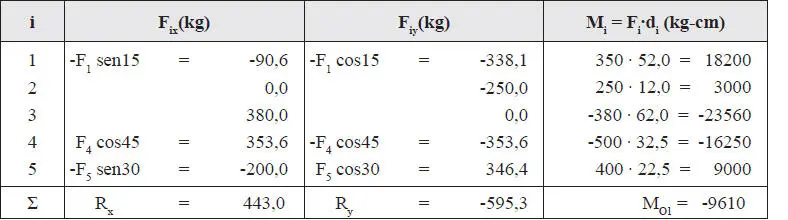
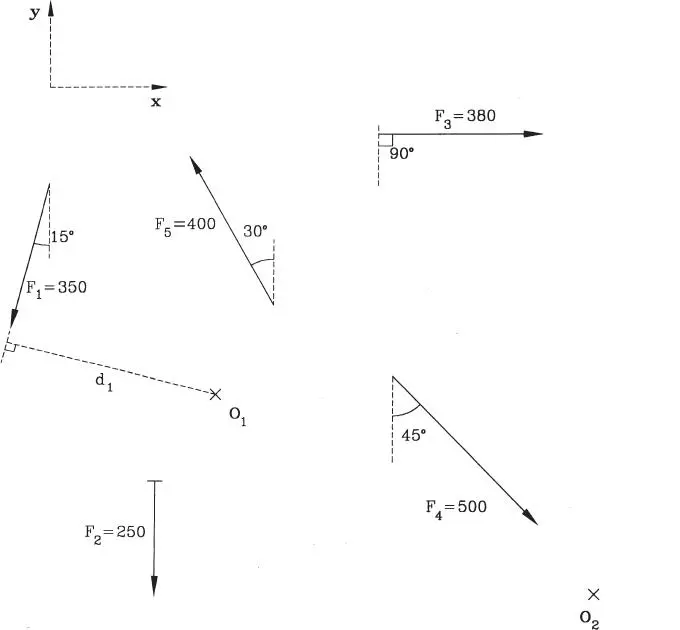
Figura E1.18.a

La última línea de la tabla es la suma de las 5 líneas anteriores. La resultante total R es entonces (Fig. E1.18.b):

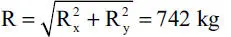
que forma ángulo α con la horizontal

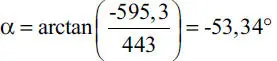
El sistema de fuerzas dado es equivalente a R actuando en O 1junto al momento M O1como muestra la Fig. E1.18.b. Notar que M O1se puso en su sentido verdadero a favor de los punteros del reloj, por ello en la figura se ha omitido el signo negativo del resultado de la Tabla.

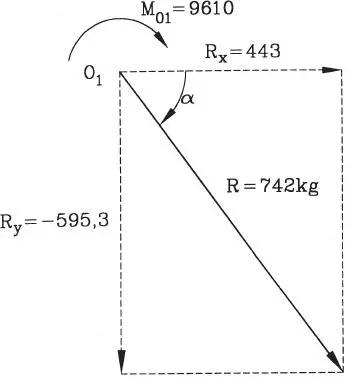
Figura E1.18.b

b) Lo que se pide es trasladar el sistema resultante en O 1(Fig. E1.18.b) al punto O 2. Para ello hay que dibujar a escala la resultante R en la Fig. E1.18.a y medir la distancia de su línea de acción al punto O 2. Esto no se muestra aquí, pero se obtiene d=22 cm, pasando la línea de acción de R hacia la izquierda del punto O 2. La nueva resultante en O 2es la misma R anterior, pero el momento en O 2es:

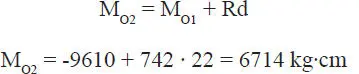
Los sistemas {R O1, M O1} y {R O2, M O2} son estáticamente equivalentes entre sí y equivalentes al sistema original dado:

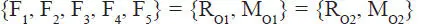
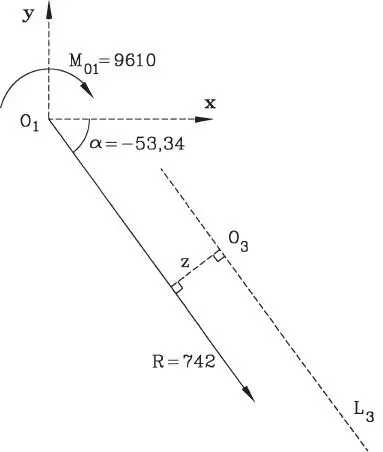
Figura E1.18.c

c) Volviendo al sistema reducido de la Fig. E1.18.b, se ve en la Fig. E1.18.c que si la resultante se traslada a la línea de acción L 3a distancia z tal que

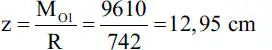
se tiene que en la nueva posición el sistema tiene la misma resultante R pero el momento, por ejemplo con respecto al punto O 3es:

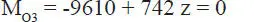
Entonces el sistema originalmente dado se ha reducido a su expresión más simple, una única fuerza R=742 kg actuando en la línea de acción L 3y un momento nulo:

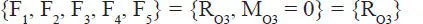
d) El cuerpo no está en equilibro porque a pesar de haberse anulado el momento persiste una resultante R=R O3≠0.

1.8.6 Equilibrio de un Cuerpo Rígido

Como puede anticiparse de la discusión y ejemplo de la Sección anterior un cuerpo estará en equilibrio cuando el sistema de fuerzas que actúa sobre él corresponda a un sistema nulo: tanto la fuerza resultante como el momento resultante son ambos nulos. Obviamente esto es lo que requiere la 2 aLey de Newton para que el sistema permanezca en reposo sin experimentar aceleración traslacional ni angular (aceleraciones asociadas a desplazamiento y rotación respectivamente).

Se tiene entonces que es condición necesaria y suficiente para el equilibrio de un cuerpo rígido sometido a un sistema cualquiera de n fuerzas externas F i, que la resultante de las fuerzas sea nula , y que la suma de los momentos de las fuerzas con respecto a un punto O arbitrario sea también nula. Simbólicamente, las condiciones anteriores se escriben como

teniendo presente que las cantidades involucradas en las sumatorias anteriores son vectoriales y no pueden sumarse en forma algebraica directa. La Ec. 1.46 es la misma que la Ec. 1-29 condición equilibrio de una partícula. Para el caso de un cuerpo rígido debe cumplirse también la Ec. 1-47 que en el caso de una partícula se satisface automáticamente porque las fuerzas son concurrentes.

Como se discutió en la Sección 1.5, la Ec. 1-46 es equivalente a tres ecuaciones escalares (Ecs. 1-30 ó 1-31) que corresponden a las condiciones de equilibrio en términos de las componentes (o proyecciones) de las fuerzas con respecto a cada uno de los ejes de un sistema de coordenadas tridimensional. Del mismo modo, la ecuación de momentos (Ec. 1-47) equivale también a tres ecuaciones escalares en términos de las componentes (o proyecciones) de los momentos con respecto al sistema de referencia tridimensional. En resumen, las ecuaciones escalares de equilibrio de un cuerpo rígido en el espacio son seis .