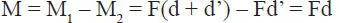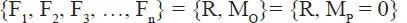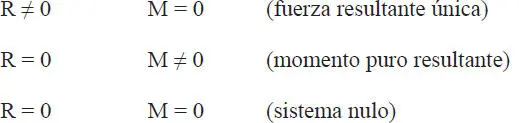Rafael Riddell Carvajal - Fundamentos de ingeniería estructural para estudiantes de arquitectura

Se denomina pareja de fuerzas a dos fuerzas de igual magnitud, de líneas de acción paralelas, y sentido opuesto. Ejemplo de una pareja es la que actúa sobre el bloque de la Fig. 1.44. Para entender el efecto de una pareja considérese la de la Fig. 1.47.a. A continuación se aplica la operación descrita en la sección anterior, trasladando la fuerza en la línea de acción L 1a la línea de acción L 2. El resultado de esta operación se muestra en la Fig. 1.47.b. Los sistemas de las Figs. 1.47.a y b son obviamente estáticamente equivalentes. Pero en el sistema de la Fig. 1.47.b las dos fuerzas opuestas actuantes en la línea de acción L 2se anulan entre sí, luego, el sistema de la Fig. 1.47.b es equivalente a un momento único M=Fd o momento puro como ilustra la Fig. 1.47.c. Como este último sistema es estáticamente equivalente al de la Fig. 1.47.a se concluye que una pareja de fuerzas es equivalente a un momento puro, es decir una acción con fuerza resultante nula pero que tiende a producir un giro del cuerpo sobre el cual se aplica.

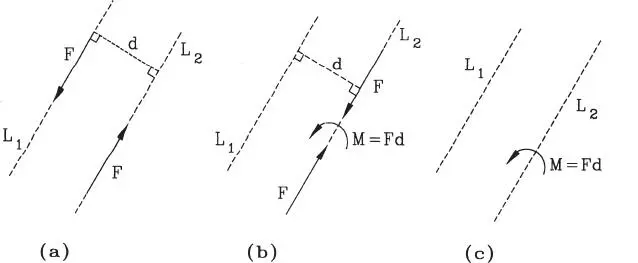
Figura 1.47Pareja de fuerzas

Figura 1.48Ejemplos de momentos puros

La acción de momento puro es muy usual y nuestros dedos la realizan con gran habilidad en múltiples ocasiones: para girar la perilla del volumen de una radio, para sacar o poner la tapa de un frasco, para retirar un tornillo suelto. También se utilizan herramientas especiales para ejercer momentos puros, como la llave sacabujías o la llave de cruz para soltar o apretar los pernos de las ruedas de un vehículo. La Fig. 1.48 muestra un par de estos ejemplos, en el caso de la tapa del frasco, los 5 dedos ejercen fuerzas tangenciales a ella, posiblemente de distintas magnitudes, las que sumadas tienen resultante nula, pero ejercen un momento puro para atornillar o desatornillar la tapa; notar que el efecto del momento es producir un giro en torno a un eje perpendicular a la tapa. Por su parte, el mecánico aplica fuerzas iguales y contrarias, que ejercen un momento puro neto sobre la tuerca; nuevamente una acción que produce un giro en torno al eje de la herramienta y al eje del perno.

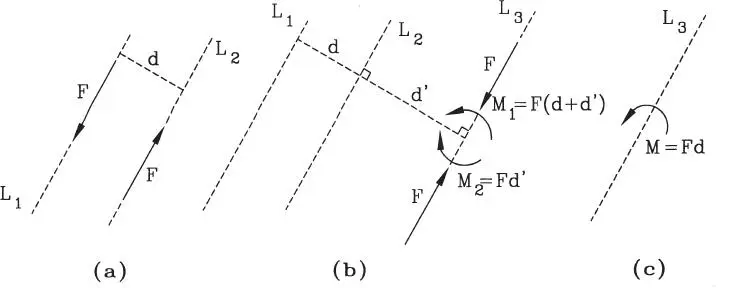
Figura 1.49

Una propiedad fundamental de una pareja de fuerzas es que puede trasladarse a cualquier posición en el plano y su efecto, desde el punto de vista del equilibrio, es el mismo. En el ejemplo de la Fig. 1.47 se hizo ver que la pareja dada era equivalente a un momento puro en torno a cualquier punto de la recta L 2. Tomando la misma pareja inicial (Fig. 1.49.a) se trasladarán ambas fuerzas, desde L 1y L 2respectivamente a una tercera línea de acción paralela L 3, a distancia d’ de L 2, y contenida en el plano de L 1y L 2, es decir, en el plano de la pareja (Fig. 1.49.b). El traslado de F de L 1a L 3incorpora el momento M 1=F(d + d’), y el traslado de F de L 2a L 3incorpora el momento M 2=Fd’. En L 3las fuerzas F de sentido opuesto se cancelan, y los momentos se suman algebraicamente pues M 2tiene sentido contrario a M 1, luego el momento puro resultante es:

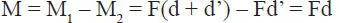
Es decir, la pareja original es equivalente a un momento puro en L 3(Fig. 1.49.c). Obviamente la operación anterior puede hacerse a cualquier recta L 3contenida en el plano de la pareja original, es decir para cualquier valor de la distancia d’, y el resultado será el mismo: un momento puro M=Fd. Se concluye entonces que el efecto de una pareja de fuerzas es equivalente a un momento puro actuando en cualquier posición del plano de la pareja; esta propiedad se conoce como principio de transmisibilidad de una pareja de fuerzas . Es decir el momento equivalente a la pareja reside en cualquier parte del plano, así como una fuerza reside en cualquier parte de su línea de acción. Por otra parte, el valor invariante Fd corresponde a la magnitud de la pareja, lo que significa que la intensidad del momento puede variarse modificando la magnitud de la fuerza F, o la distancia d, o ambas. Finalmente, como ya se mencionó, un momento tiene también sentido (claramente al mover la perilla de la radio podemos hacerlo en uno u otro sentido). Típicamente, en el plano se utiliza con frecuencia la identificación del sentido de un momento como a favor de los punteros del reloj , o en el caso opuesto, en contra de los punteros del reloj .

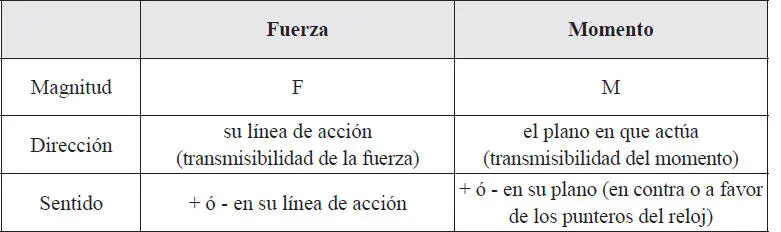
En conclusión, el ente momento es similar al ente fuerza . Ambos tienen las propiedades de magnitud, dirección, y sentido, como se comparan en la Tabla 1.2.

Finalmente, cabe mencionar que el plano que alberga a un momento puede tener dirección cualquiera en el espacio y puede ser necesario expresar el momento en sus componentes según los ejes de un sistema de referencia tridimensional. Sin embargo, conforme a los objetivos de este texto y por simplicidad, aquí se trabajará casi exclusivamente con problemas planos que no requieren la representación vectorial de los momentos.

TABLA 1.2Comparación de los entes Fuerza y Momento

1.8.5 Reducción de un Sistema General de Fuerzas. Caso Plano

Dado un sistema de fuerzas cualquiera en un plano, su reducción consiste en simplificarlo a una fuerza única R y a un momento único M Oen torno a un punto arbitrario O previamente escogido, de modo que el sistema original y el sistema resultante son estáticamente equivalentes:

El procedimiento consiste en aplicar la operación descrita en la Sección 1.8.3 para todas las fuerzas dadas, trasladando cada una de ellas a una línea de acción que pasa por el punto O. Finalmente se tiene un conjunto de fuerzas concurrentes en O, para el cual se obtiene su resultante R, más el conjunto de momentos de cada una de las fuerzas en torno al punto O, cuya suma algebraica es el momento total M O. En general el sistema reducido será tal que R≠0 y M O≠0, sin embargo, en el caso de un sistema de fuerzas plano, el sistema resultante puede siempre transformarse en uno referido a un nuevo punto P tal que M P=0 y

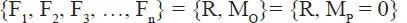
Existen entonces tres alternativas para el sistema reducido resultante:

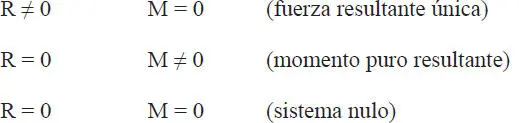
por cierto el último caso corresponderá a lo que se llama un sistema de fuerzas en equilibrio. El procedimiento de reducción de un sistema de fuerzas plano se ilustra en el ejemplo siguiente.