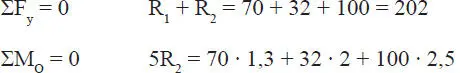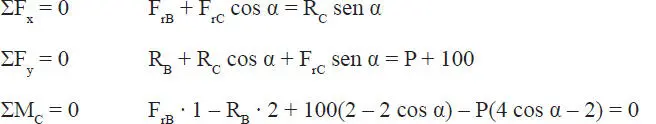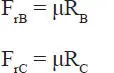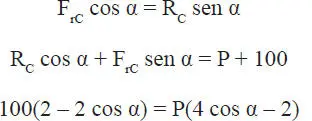Rafael Riddell Carvajal - Fundamentos de ingeniería estructural para estudiantes de arquitectura

Un gran número de casos de equilibrio de cuerpos rígidos en el espacio pueden tratarse como problemas planos , e incluso, cuando tal simplificación no es posible, los problemas pueden al menos parcialmente descomponerse para ser analizados en varios planos separadamente. Por problema plano se entiende aquel en que las fuerzas del sistema pueden suponerse contenidas en un plano, aunque no necesariamente los cuerpos involucrados sean planos (como por ejemplo el caso de la Fig. 1.33.c). Con frecuencia también se presentan casos en que el espesor del problema, o su tercera dimensión, es despreciable frente al tamaño de los cuerpos en el plano de sus dos dimensiones predominantes, como se discutirá más adelante en relación con el equilibrio de estructuras “planas”. La simplicidad de los problemas planos los hace particularmente atractivos para madurar los conceptos fundamentales de equilibrio; su simplicidad radica en que las Ecs. 1-46 y 1-47, que como se dijo antes representan seis ecuaciones escalares, se reducen a tres. En efecto, si el plano de las fuerzas del sistema es el plano xy, la tercera de las Ecs. 1-46 (Ec. 1-30.c ó 1-31.c) es irrelevante, por su parte, de las tres ecuaciones de momento, sólo queda una. Las condiciones de equilibrio de un cuerpo rígido plano son entonces:

en que O es punto cualquiera del plano de las fuerzas.

Ejemplo 1.19

Un hombre y un niño de pesos 70 y 32 kg respectivamente se encuentran sobre una pasarela provisoria de 100 kg de peso y 5 m de longitud como muestra la Fig. E1.19.a. Determinar las reacciones en los apoyos de la viga.

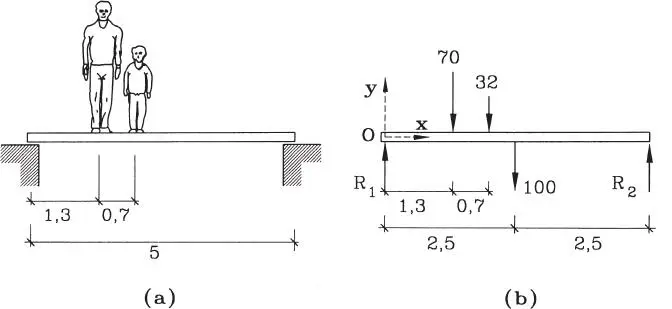
Figura E1.19

Solución:La Fig. E1.19.b muestra el modelo de cuerpo libre de la viga indicando las fuerzas que actúan sobre ella. Se han supuesto sólo dos fuerzas de reacción verticales en los extremos de la viga, ya que no hay solicitaciones horizontales. A las reacciones se les ha supuesto un sentido hacia arriba, opuesto al sentido de las cargas gravitacionales. Las ecuaciones de equilibrio relevantes son las Ecs. 1-48.b y c:

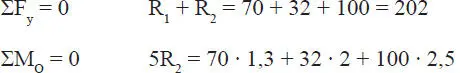
de la segunda ecuación se obtiene R 2=405/5=81 kg, valor que introducido en la primera da R 1=121kg.

Ejemplo 1.20

A una barra homogénea de 4 m de longitud y 100 kg de peso, que se apoya como se muestra en la Fig. E1.20.a, se le aplica una carga vertical P en su extremo A. Los contactos son rugosos con coeficiente μ=0,6. Se pide: a) Plantear las ecuaciones de equilibrio; b) Estudiar para que valor de P se rompe el equilibrio (por deslizamiento de la barra o porque su extremo B se levanta del piso).

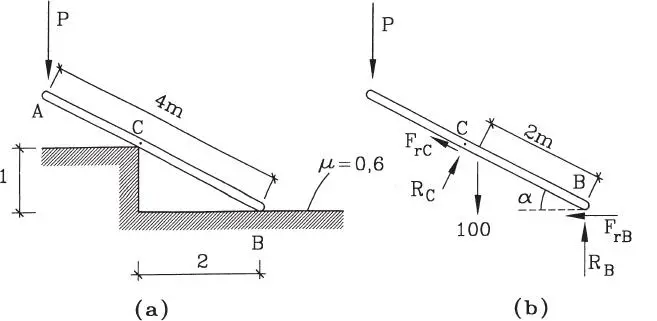
Figura E1.20

Solución:La Fig. E1.20.b muestra el diagrama de cuerpo libre de la barra con todas las fuerzas externas que actúan sobre ella. Las reacciones R Cy R Bson las “normales” (perpendiculares) a los planos de deslizamiento tangencial, y las fuerzas de roce F rBy F rCson por supuesto tangenciales, es decir perpendiculares a las normales, y de sentido opuesto al deslizamiento potencial. El peso de la barra actúa en su centro de gravedad (punto medio). El ángulo α es conocido pues tgα=l/2, o sea α=26,565º.

a) Las ecuaciones de equilibrio (Ecs. 1-48) son las siguientes:

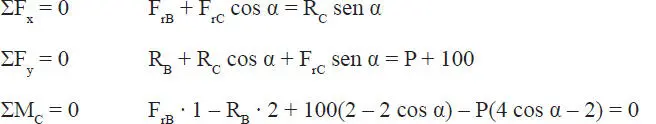
La primera observación que procede hacer es que este sistema de 3 ecuaciones tiene 5 incógnitas: P y las 4 componentes de reacción, luego no puede resolverse. Incluso si la fuerza P fuera un dato conocido tampoco podrían calcularse las 4 reacciones incógnitas. Por ello, las condiciones a que se refiere la parte “b” del problema deberán aportar nuevas ecuaciones que permitan resolver el sistema de ecuaciones.

b) Caso de deslizamiento de la barra:

La condición de deslizamiento corresponde al caso límite de equilibrio, luego se cumple que:

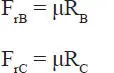
dos ecuaciones adicionales que sumadas a las 3 anteriores permiten resolver para las 5 incógnitas antes mencionadas, obteniéndose: R B=-19,18 kg, F rB=-11,51 kg, R C=128,64 kg, F rC=77,18 kg, P=30,40 kg. Pero, la reacción R Bno puede ser negativa, ya que el piso no podría ejercer una fuerza de ese sentido pues antes la barra se levantaría despegándose del piso en el punto B. Este es justamente el segundo caso que hay que analizar, ya que la situación de deslizamiento no ocurre.

c) Caso de levantamiento de la barra en B:

El diagrama de la Fig. E1.20.b sigue siendo válido con la modificación que R By F rBno existen pues no hay contacto en B. O sea, se ha supuesto que se está justo iniciando el despegue del extremo B de la barra que se encuentra a una distancia ínfima del piso.

Las ecuaciones de equilibrio se obtienen de las mismas anteriores haciendo R B=0 y F rB=0. Se tiene entonces:

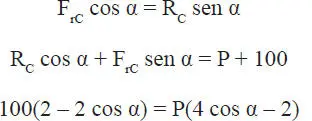
sistema de 3 ecuaciones con 3 incógnitas de donde se obtienen P= 13,38 kg, R C=101,41 kg, y F rC=50,71 kg. Lo que indica que para P=13,38 se rompe el equilibrio por levantamiento del extremo B de la barra. Notar también que cuando esto ocurre F rC≠μR C, como era de esperar, porque esta situación no tiene nada que ver con una condición límite de equilibrio por deslizamiento.

Ejemplo 1.21

Una escalera de 3 m de largo y peso 35 kg se apoya formando un ángulo de 60º como se muestra en la Fig. E1.21.a. La pared es lisa pero existe fricción con el suelo con coeficiente de roce μ. Se pide: a) Determinar las reacciones en el piso y en el muro cuando un hombre de 75 kg de peso sube hasta una distancia de 2 m medida desde el extremo inferior de la escalera; b) Determinar el coeficiente de roce μ necesario para que el hombre pueda llegar al extremo superior de la escalera.

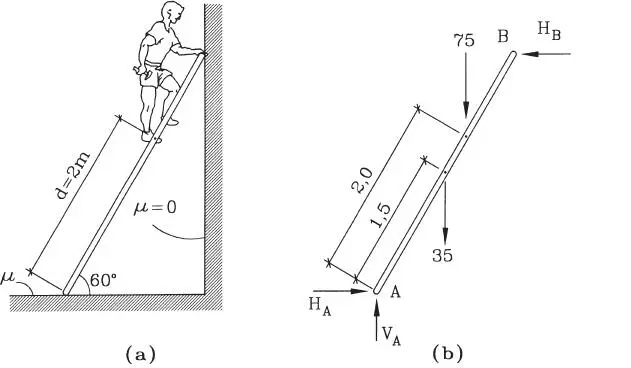
Figura E1.21

Solución:La Fig. E1.21.b muestra el diagrama de cuerpo libre de la escalera. La reacción en B es perpendicular al muro por ser contacto liso. En la base A existe tanto reacción normal V Acomo componente tangencial de roce H A.