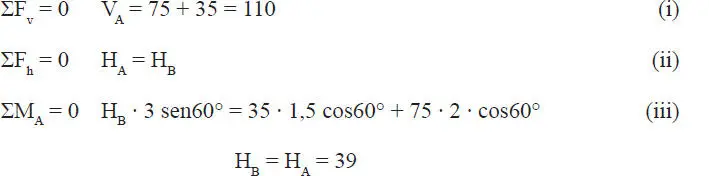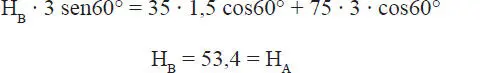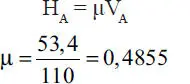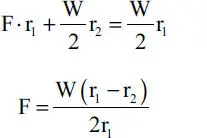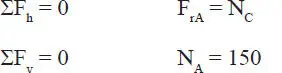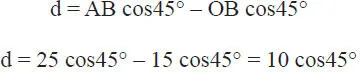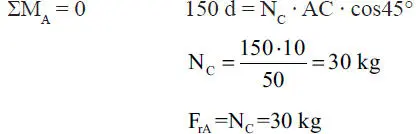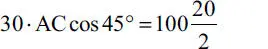Rafael Riddell Carvajal - Fundamentos de ingeniería estructural para estudiantes de arquitectura

a) Las ecuaciones de equilibrio de fuerzas verticales, horizontales y momentos son respectivamente:

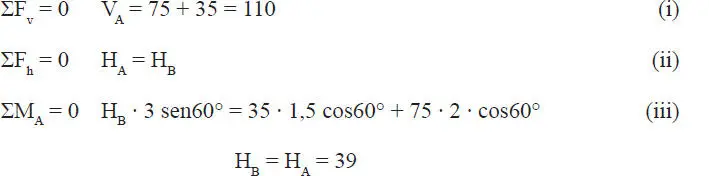
b) Considérese que cuando el hombre llega arriba se alcanza el estado límite de equilibrio. Las ecuaciones i e ii son las mismas anteriores. En la ecuación iii sólo se modifica la distancia d que ahora es 3 m, luego:

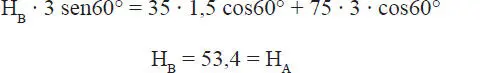
Notar como aumenta la fuerza de roce a medida que el hombre sube. En la condición límite de equilibrio el roce alcanza el valor máximo que puede desarrollar, o sea:

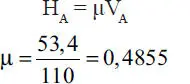
Naturalmente para este valor del coeficiente de roce la escalera estará “a punto de deslizar” cuando el hombre llegue al extremo superior. Si se desea evitar el riesgo de caída, debería haber un coeficiente de roce mayor que el valor mínimo necesario calculado. Sin embargo, puede pensarse que en una situación real también existirá rugosidad en el contacto con el muro, y la fuerza de roce correspondiente ayudará al equilibrio. Como ejercicio el lector puede rehacer el problema pero con fricción tanto en A como en B. Se dará cuenta que no puede resolver la parte “a”, ¿por qué?. Al resolver la parte “b” por cierto encontrará que el coeficiente de roce necesario es menor que el antes calculado.

Ejemplo 1.22

La Fig. E1.22.a muestra un tecle, que es un aparejo para levantar objetos de gran peso en forma manual. Típicamente el tecle se cuelga de un marco móvil que permite trasladarlo a distintos lugares en un taller; en la figura se muestra suspendido de un techo fijo. La parte superior del aparato se compone de dos poleas solidarias (unidas a un mismo eje) de radios diferentes. Una cadena sin fin pasa por las poleas, las que son dentadas para enganchar los eslabones de la cadena e impedir su deslizamiento. Al tirar el hombre de la cadena, las poleas superiores giran juntas, pero el punto A de la polea de radio mayor avanza más que el punto B de la de radio menor, lo que tiene por efecto que la polea C y la carga suban. Notar que el hombre tira hacia un lado de la cadena y el otro lado queda suelto. Si los radios de las poleas solidarias son r 1=10 cm y r 2=8 cm, determinar la fuerza que debe hacer el hombre para levantar un peso W=300 kg. Despreciar los pesos de la cadena y de las poleas.

Solución:Del diagrama de cuerpo libre de la polea C (Fig. E1.22.b), despreciando el peso de la polea, se tiene que las cadenas que la soportan realizan cada una fuerzas de W/2. Estas fuerzas se transmiten a la polea superior como se muestra en la Fig. E1.22.c. Hacia el lado de la cadena suelta, la fuerza es Q=0, ya que se está despreciando el peso de la cadena. La fuerza que realiza el hombre es F; nuevamente, despreciando el peso de la cadena, F actúa como se indica en la Fig. E1.22.c. Tomando momentos en tomo al punto O se tiene:

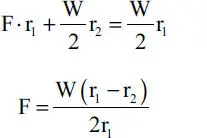
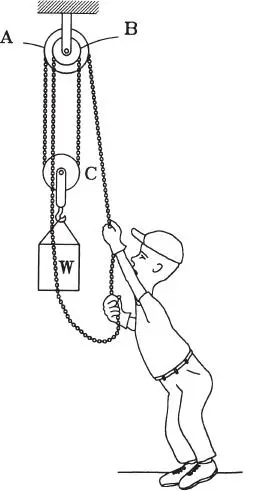
Figura E1.22.a

Notar que si r 2se aproxima a r 1la fuerza F se hace cada vez más pequeña. En particular si r 2=r 1resulta F=0, es decir el hombre no realizaría esfuerzo, pero el aparato sería inútil porque la carga no subiría aunque se dieran vueltas y vueltas a la cadena. Para los datos especificados en el enunciado se obtiene

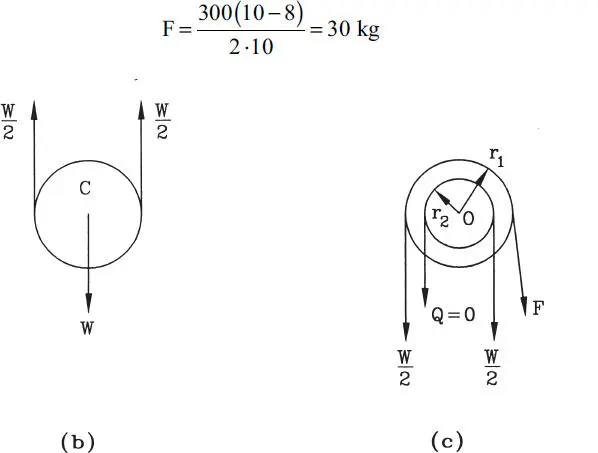
Figura E1.22(continuación)

Ejemplo 1.23

Un cajón homogéneo de 150 kg de peso ha volcado apoyándose en otro cajón de 100 kg de peso. El coeficiente de fricción de los cajones con el suelo es μ=0,4. El contacto entre ambos cajones es liso. Determinar si el sistema está en equilibrio.

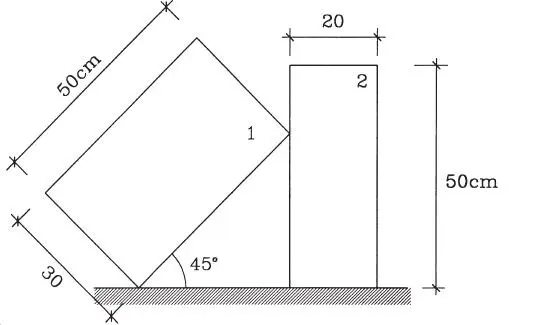
Figura E1.23.a

Solución:

i) Equilibrio del cajón 1

La Fig. E1.23.b muestra el diagrama de cuerpo libre del cajón 1. En el piso hay reacciones normal y de roce, no así en C donde el contacto es liso. Las ecuaciones de equilibrio de fuerzas son:

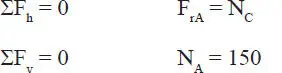
La ecuación de momentos conviene tomarla con respecto al punto A; para ello hay que calcular previamente la distancia “d” de la fuerza de 150 kg al punto A:

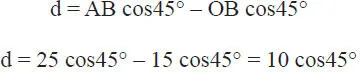
luego:

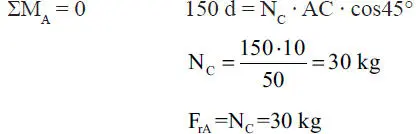
La máxima fuerza de roce que puede desarrollarse es F rmax=μN A=0,4·150=60 kg; como F rArmaxel cajón 1 está en equilibrio.

ii) Equilibrio del cajón 2

Este cuerpo podría perder el equilibrio de dos formas: por deslizamiento o por volcamiento. Para analizar el deslizamiento considérese la Fig. E1.23.c; las ecuaciones de equilibrio de fuerzas son:

La fuerza de fricción máxima que puede desarrollarse es F rmax=μN=0,4·100=40 kg; como F rrmaxel cajón 2 no desliza.

Para analizar el volcamiento considérese la Fig. E1.23.d. El volcamiento ocurrirá por giro en torno a la arista D del cajón, tendiendo éste a levantarse manteniendo contacto con el suelo solamente a través de la arista D. Por ello, las reacciones del piso deberán actuar justo en D. Las ecuaciones de equilibrio de fuerzas son las mismas anteriores. La ecuación de equilibrio de momentos en torno a D requeriría:

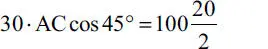
lo que no se cumple porque 1060,7≠1000, luego el cajón 2 vuelca. Entonces el cajón 1 tampoco está en equilibrio porque no puede afirmarse en el cajón 2.

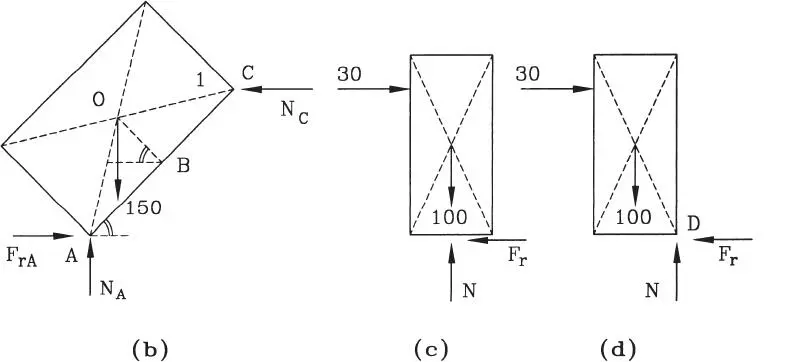
Figura E1.23(continuación)

1.9 Ejercicios Propuestos

1.01 Localizar los centros de gravedad de los alambres delgados que se indican en la figura. (Respuesta: x*=-3b/34, y*=45b/272; x*=6,71 cm, y*=17,95 cm)