Rafael Riddell Carvajal - Fundamentos de ingeniería estructural para estudiantes de arquitectura

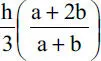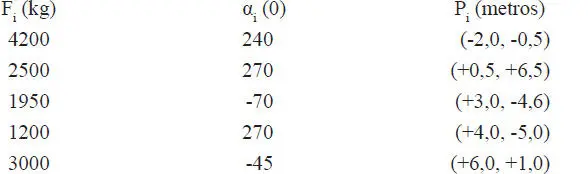
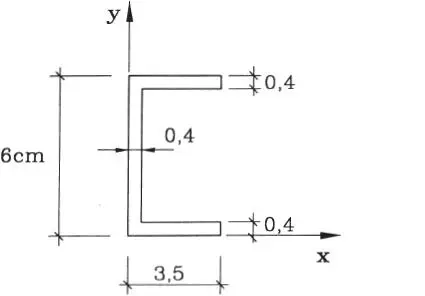
1.02 Hallar el centro de gravedad del área mostrada en la figura. (Respuesta: x*= 1,09 cm, y*=3 cm)

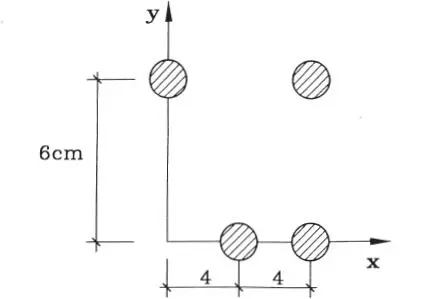
1.03 Encontrar el centro de gravedad de los 4 círculos de radio 1 cm ubicados como se indica. (Respuesta: x*=5 cm, y*=3 cm)

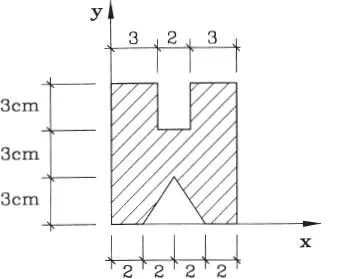
1.04 Encontrar el centro de gravedad de la superficie sombreada de la figura. (Respuesta: x*=4 cm, y*=4,55 cm)

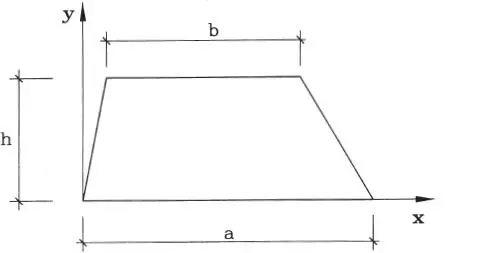
1.05 Demuestre que el centro de gravedad de un área trapecial de bases a y b y altura h tiene una coordenada y* igual a

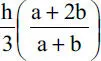
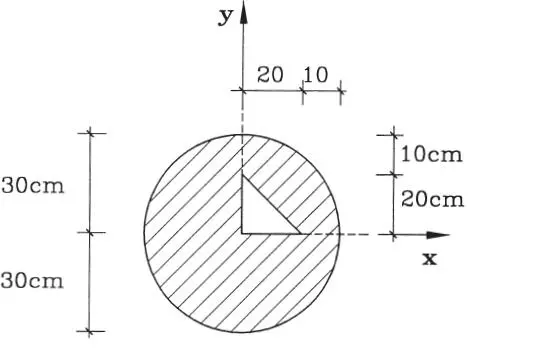
1.06 Encontrar el centro de gravedad del área de la figura achurada (usar centro de gravedad de un sector semicircular de Tabla V.2). (Respuesta: x*=17,88 cm, y*=38,47 cm)

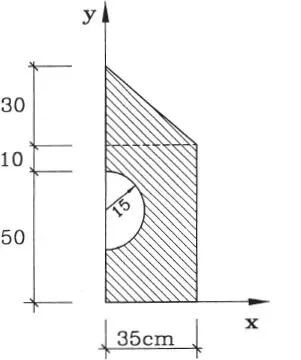
1.07 Un disco de radio r 1=50 cm y espesor unitario tiene cuatro agujeros como se muestra en la figura. Los centros de los agujeros están sobre una circunferencia de radio r 2=30 cm formando ángulos de 60º. Determine el centro de gravedad del disco en el plano x, y. (Respuesta: x*=13 r 2 3/(625–r 2 3), y*=0 cm)

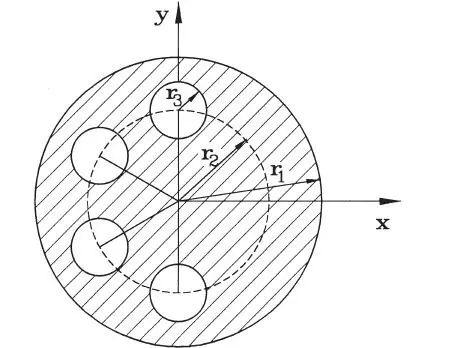
1.08 Encontrar el centro de gravedad del área de la figura achurada. (Respuesta: x*=8,4 cm, y*=4,7 cm)

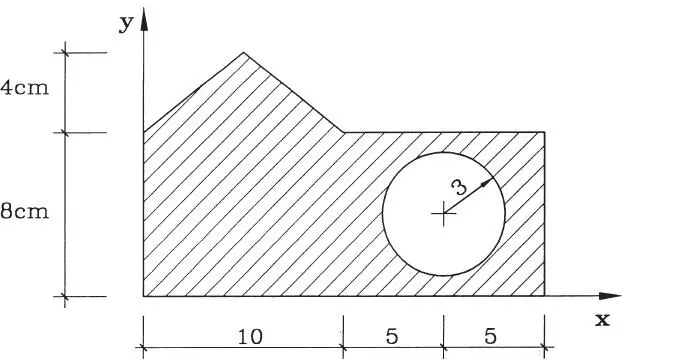
1.09 Determinar el centro de gravedad de una placa circular de material homogéneo y espesor constante con una perforación triangular como se muestra. (Respuesta: x*=y*= -0,5074)

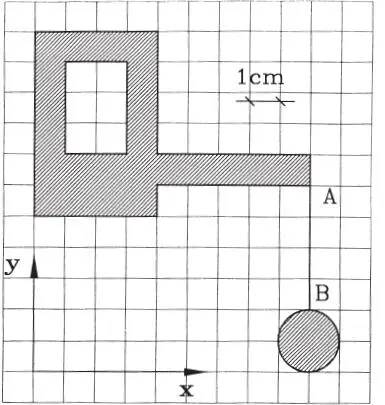
1.10 Determinar las coordenadas del centro de gravedad del cuerpo plano que se indica, el cual está dibujado a escala. Cada cm 2de área (achurada) pesa 15 gramos y cada cm de longitud de la barra AB pesa 5 gramos. (Respuesta: x*=3,95 cm, y*=6,62 cm)

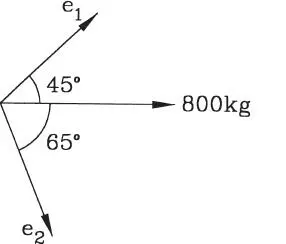
1.11 Descomponga la fuerza de 800 kg en dos componentes a lo largo de las direcciones e 1y e 2indicadas. Use solución gráfica y compruebe analíticamente. (Respuesta: F 1=771,58 kg, F 2=601,99 kg)

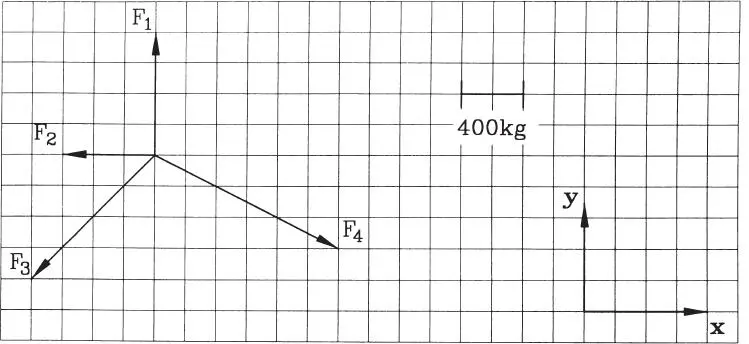
1.12 Sobre una partícula actúa el sistema de fuerzas F 1=800 kg, F 2=600 kg, F 3=1131,4 kg y F 4= 1341,6 kg. Determinar la resultante del sistema e indicar cuáles son sus componentes en las direcciones x e y. Determinar las componentes de la resultante en un nuevo sistema de ejes x’ y’ correspondiente al sistema xy original girado en 45° en sentido trigonométrico positivo. Use solución gráfica y compruebe analíticamente. (Respuesta: F x= -200 kg, F y= -600 kg, F x’= -565,69 kg, F y’= -282,84 kg)

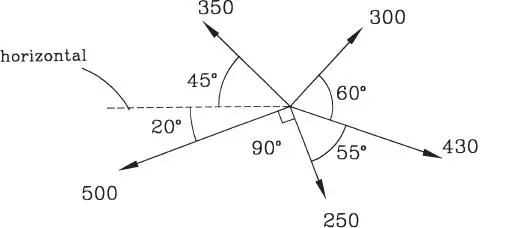
1.13 Sobre una partícula actúa el sistema de 5 fuerzas coplanares indicado. Se pide: a) determinar analíticamente su resultante, b) dibujar el polígono de fuerzas y su resultante. (Respuesta: R=57,77, α=265,7º)

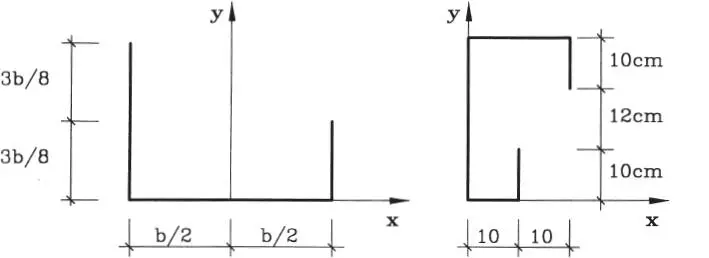
1.14 Sea un sistema de fuerzas F ique actúan en un plano vertical, formando ángulos α imedidos desde la dirección x horizontal, y aplicadas en los puntos P icuyas coordenadas se indican. Usando el polígono funicular determinar gráficamente la resultante e indicar el punto de coordenadas (x, 0) por donde pasa la línea de acción de la resultante.

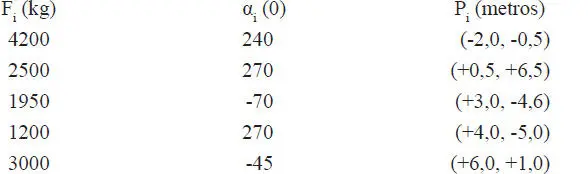
1.15 Sobre un soporte fijo a la pared actúan las fuerzas F 1=50, F 2=80 y F 3=90 formando ángulos α=31° y β=60°. Determine: a) la magnitud y dirección de la resultante R = {F 1, F 2, F 3}, b) las componentes horizontal y vertical de R y dibújelas actuando sobre el soporte en sus sentidos positivos, c) las reacciones V y H de la pared sobre el soporte y dibújelas actuando sobre el soporte en sus sentidos positivos. (Respuesta: R=175,8, α=17,27°, R H=167,9, R v=52,2)

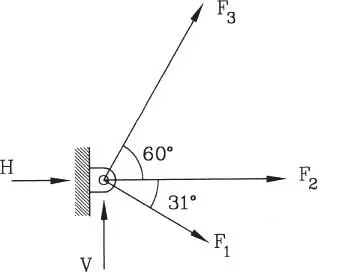
1.16 Determinar la resultante del sistema de fuerzas paralelas dado: a) mediante solución geométrica utilizando polígono funicular, b) utilizando el concepto de centro de gravedad.

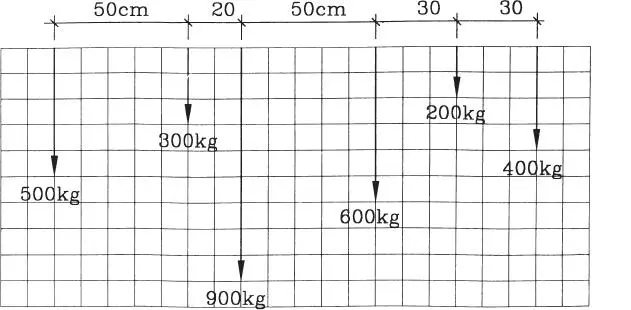
1.17 Un bloque de peso W se sostiene mediante dos cables livianos. Determinar las fuerzas en los cables. (Respuesta: 0,879W; 0,652W)

1.18 Una esfera que pesa 10 kg y tiene 15 cm de radio cuelga de un cable liviano y se apoya sobre una pared lisa. Determinar la fuerza T en el cable y la reacción de la pared sobre la esfera. (Respuesta: 10,44; 3)

1.19 Sobre una pequeña rueda que puede moverse libremente sobre un hilo liviano se aplica una fuerza P. Demuestre que sólo hay equilibrio si α=7,5º, y que en el estado de equilibrio la fuerza de tracción del cable es 82,1% de P.