Rafael Riddell Carvajal - Fundamentos de ingeniería estructural para estudiantes de arquitectura

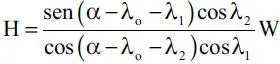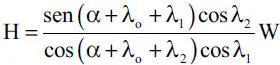
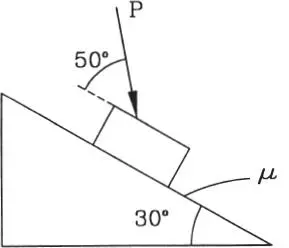
1.35 A un bloque de peso 100 kg que se encuentra sobre un plano inclinado en 30° se le aplica una fuerza P=20 kg como se indica. El coeficiente de fricción entre los cuerpos es 0,65. Verificar si el bloque está en equilibrio. (Respuesta: sí)

1.36 Dos bloques de peso W unidos por una cuerda liviana están montados como muestra la figura. Verificar si están en equilibrio. (Respuesta: sí)

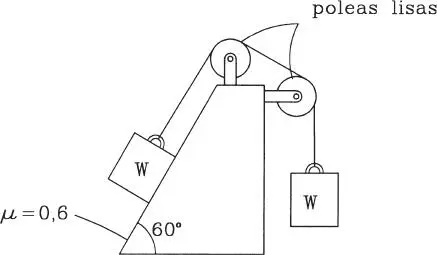
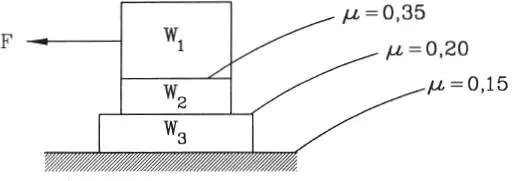
1.37 En el sistema de la figura los contactos entre los bloques y los planos en que se apoyan son rugosos con coeficiente de roce igual a 0,3. La cuerda sin peso que une los bloques pasa por una polea lisa. Se pide: a) Si P=0, ¿está el sistema en equilibrio?, b) ¿Qué valor de P se requiere para hacer deslizar los bloques?. (Respuesta: no; 1,82W)

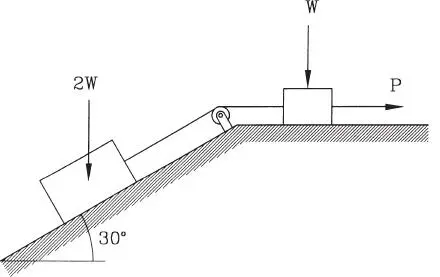
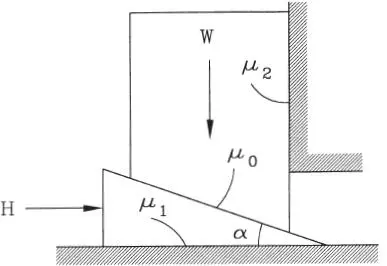
1.38 Sobre una cuña sin peso que sostiene un bloque de peso W se aplica una fuerza horizontal H. Existe rugosidad en todos los contactos con coeficientes de roce μ 0=tanλ 0, μ 1=tanλ 1y μ 2=tanλ 2. Demostrar que la mínima fuerza H necesaria para mantener el equilibrio es y la fuerza H necesaria para levantar el bloque es

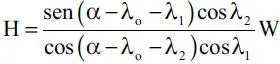
y la fuerza H necesaria para levantar el bloque es

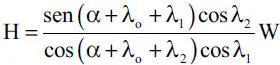
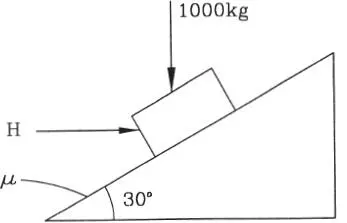
1.39 Sobre un bloque de 1000 kg de peso, que descansa sobre un plano inclinado en 30°, se aplica una fuerza horizontal H. El coeficiente de roce entre el bloque y el plano es μ=0,5. Determinar la magnitud de H requerida para: a) mantener el equilibrio, b) que la fuerza de fricción sea nula, c) iniciar el deslizamiento del bloque hacia arriba. (Respuesta: 60 kg, 577 kg, 1514 kg)

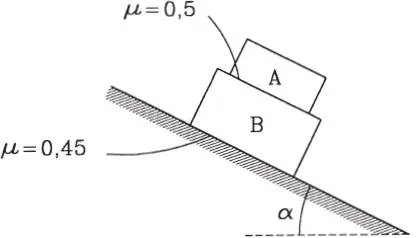
1.40 Los bloques A y B de 30 y 20 kg de peso respectivamente, descansan en equilibrio en un plano inclinado en α=20°. Los coeficientes de fricción son los indicados. Se pide: a) Determinar las fuerzas reactivas sobre los bloques A y B; b) Si se aumenta la inclinación del plano inclinado, ¿para qué ángulo α se rompe el equilibrio? ¿cómo se rompe el equilibrio?. (Respuesta: a) N A=28,19 kg, F rA=10,26 kg, N B=46,98 kg, F rB=17,l kg; α=24,2°, desliza B sobre el plano inclinado manteniéndose A solidario con B)

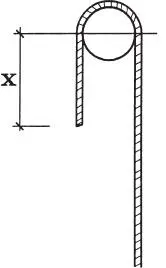
1.41 Una cuerda de 2 metros de largo que pesa 3600 gramos (1 cm de cuerda pesa 18 gr) descansa sobre un cilindro rugoso de 20 cm de diámetro y coeficiente de roce μ=0,3. Determinar el mínimo largo x necesario para mantener el equilibrio. (Respuesta: 47,3 cm)

1.42 Si se mantienen las mismas condiciones del Ejercicio 1.23, excepto que ahora la barra AB pesa 30 kg, recalcule la fuerza en el hilo y calcule las reacciones en el apoyo A. (Respuesta: T=91,9, H A=76,6, V A=79,3)

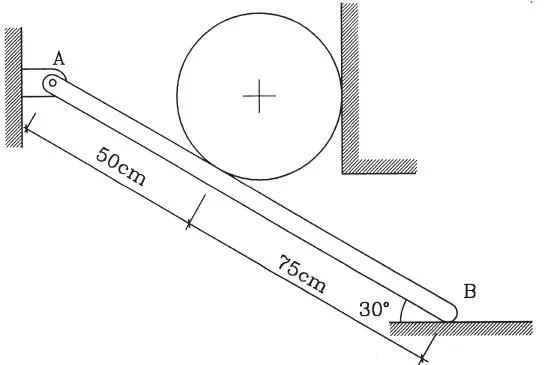
1.43 Un cilindro se apoya sobre una barra y un muro en la forma que se indica en la figura. El cilindro pesa 500 kg y la barra 100 kg. Si todas las superficies son lisas, determinar las reacciones en los apoyos A y B de la barra. (Respuesta: H A=288,7 kg, V A=283,3 kg, V B=316,7 kg)

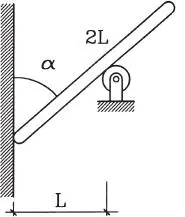
1.44 Una barra de longitud 2L y peso W se apoya en una polea lisa y en una pared rugosa. El coeficiente de fricción entre la barra y la pared es 0,5. Comprobar si para α=60° la barra está en equilibrio. (Respuesta: no)

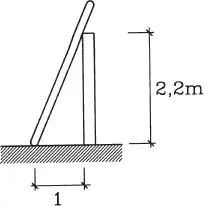
1.45 Una barra de metal de 3 m de largo y 28 kg de peso se apoya sobre un piso de baldosas mojadas, y por lo tanto muy resbaloso (contacto liso), y sobre un muro de hormigón (contacto rugoso con coeficiente de roce igual a 0,3). ¿Está la barra en equilibrio?. (Respuesta: no)

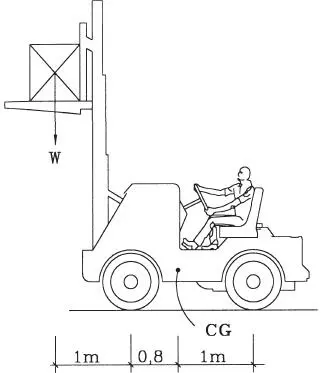
1.46 La grúa horquilla de la figura tiene una tara de 5000 kg y su centro de gravedad (CG) se ubica como se muestra. Determinar la carga neta máxima que puede levantar ubicada en la posición indicada. Determinar las reacciones en las ruedas para la carga bruta máxima. (Respuestas: W max= 4000 kg, reacciones 4500 y 0)

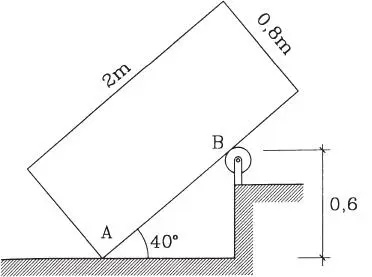
1.47 Una placa de madera de 2 metros de largo, 0,8 m de ancho y peso 25 kg, se mantiene en un plano vertical apoyándose en el piso rugoso con coeficiente de roce 0,2 y en un rodillo liso en B. El punto de contacto B está a 0,6 m de altura sobre el piso. Calcular las reacciones en B y en A. ¿Está la placa en equilibrio?. (Respuesta: N B=13,64 kg, H A=8,77 kg, V A=14,55; no)

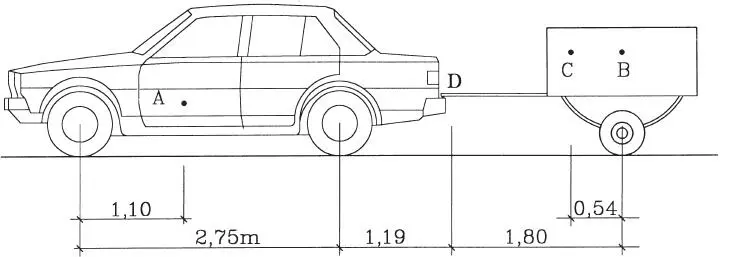
1.48 Un vehículo que pesa 1400 kg incluidos sus pasajeros remolca un carro de 180 kg de peso. La ubicación de los centros de gravedad A y B de cada uno se muestran en la figura. El carro se carga con 200 kg en bultos distribuidos en forma no-homogénea, quedando el centro de gravedad C de la carga en la posición indicada. La barra de tiro del carro puede girar libremente en torno a la rótula de enganche D. Determinar: a) Las reacciones en las ruedas del vehículo sin el carro; b) Las reacciones en todas las ruedas cuando se engancha el carro. (Respuesta: 420, 280 kg; 407, 323, 160 kg)

1.49 El sistema de la figura consta de dos barras AC y BC que pesan 240 y 113 kg respectivamente y pueden girar libremente en torno a las articulaciones A y B. Tienen contacto liso en C y se sostienen por medio de la cuerda liviana tensada por un peso W que a su vez descansa en la barra AC. Si W=1000 kg, calcular la fuerza que ejerce la cuerda y la reacción interna en C. ¿Qué valor mínimo debe tener W para que el sistema no colapse?. (Respuesta: 489,6 kg, 290 kg; 249,5 kg)