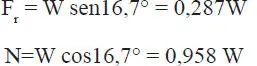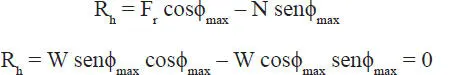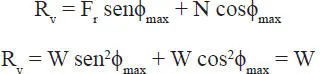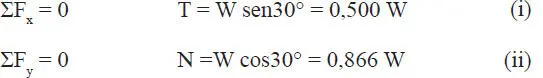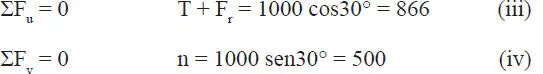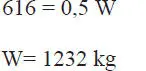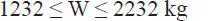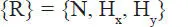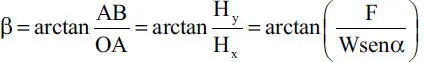Rafael Riddell Carvajal - Fundamentos de ingeniería estructural para estudiantes de arquitectura

que corresponde a la Ec. 1-39 que conduce a la misma ecuación usada antes.

c) Usando las ecuaciones de la parte (b) se tiene:

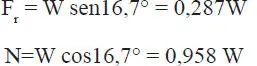
d) La reacción total es la composición (suma) de F y N (Fig. E1.13.c). La componente horizontal de R es:

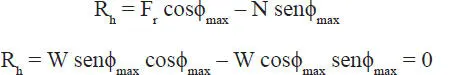
y la componente vertical es:

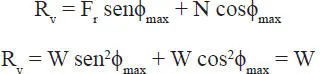
o sea, R=R V=W, lo que era obvio ya que para equilibrar el peso W vertical se requiere una reacción también vertical, de sentido opuesto y magnitud W. Este último resultado no rige sólo para la condición límite de equilibrio sino para cualquier inclinación ϕ del plano inclinado tal que ϕ≤ϕ max.

Ejemplo 1.14

Sobre dos planos inclinados en 30º y 60º descansan bloques de peso W y 1000 kg respectivamente (Fig. E1.14.a). El contacto es liso en el plano de la izquierda y rugoso con coeficiente μ=0,5 en el plano de la derecha. Los bloques están unidos por una cuerda liviana que pasa por una polea lisa en la arista C. Determinar qué valores del peso W permiten el equilibrio del sistema.

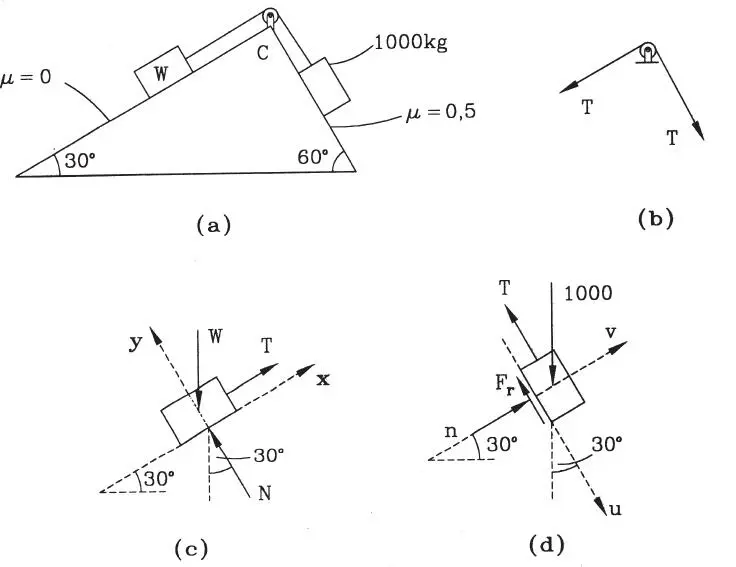
Figura E1.14

Solución:Considérese los diagramas de cuerpo libre de los tres elementos relevantes del sistema. En el caso de la polea, por ser lisa, la fuerza que transmite la cuerda se mantiene constante, y se ha designado por T (Fig. E1.14.b). En el caso del bloque de peso W (Fig. E1.14.c) la reacción del plano sobre el bloque es únicamente la normal N, ya que el contacto es liso; y las ecuaciones de equilibrio son:

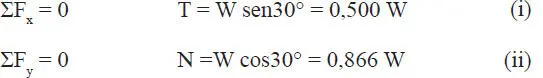
En el caso del bloque de peso 1000 kg considérese primero la condición límite de equilibrio en que el bloque tiende a deslizar hacia abajo del plano inclinado, por esta razón en la Fig. E1.14.d la fuerza de roce F r(componente tangencial de la reacción) se ha colocado en el sentido negativo del eje u, es decir, en sentido opuesto al desplazamiento potencial; en otras palabras, F rayuda a que el bloque no caiga. Las ecuaciones de equilibrio son:

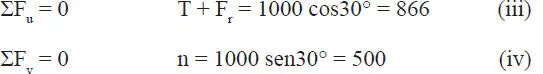
pero por ser condición límite de equilibrio y utilizando la ecuación iv se tiene

que se introduce en la ecuación iii para obtener T=866–F r=616 kg. Con este valor de T, la ecuación i queda:

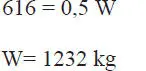
Este valor de W es el necesario para justo impedir que el bloque de 1000 kg caiga hacia abajo. Si se aumenta el valor de W se seguirá manteniendo el equilibrio (disminuyendo F r), pero si W es muy grande puede llegar a levantar el bloque de 1000 kg hacia arriba perdiéndose nuevamente el equilibrio. En este nuevo estado límite de equilibrio el diagrama de la Fig. E1.14.d sigue siendo válido, excepto que F rtiene sentido contrario pues ahora debe oponerse al deslizamiento potencial hacia arriba. Todas las ecuaciones de equilibrio antes planteadas son válidas, excepto la iii que ahora queda

Utilizando la ecuación v se obtiene T=866+F r=1116 kg, y de la ecuación i se obtiene W=2232 kg. Se concluye entonces que el sistema está equilibrio si

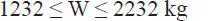
Ejemplo 1.15

A un bloque de peso W, que descansa en un plano rugoso inclinado en α con el plano horizontal, se le aplica una fuerza F horizontal paralela al plano, a) Si el sistema está en equilibrio, determinar la magnitud y dirección de la fuerza de fricción; b) Determinar la máxima fuerza F que se puede aplicar y la dirección en que se iniciará el desplazamiento al romperse el equilibrio.

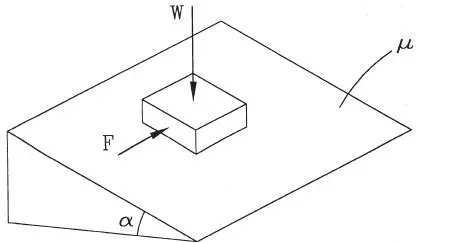
Figura E1.15.a

Solución:Este es un problema de tipo espacial por lo que deberá utilizarse un sistema de ejes de referencia tridimensional. Además, por tratarse de un cuerpo sometido a sólo 3 fuerzas (W, F y la reacción R del plano sobre él), éstas deben ser concurrentes y el cuerpo puede modelarse como partícula. Considérese entonces el sistema de ejes que muestra la Fig. E1.15.b en que el plano xy coincide con el plano inclinado, el eje z es perpendicular a él, y el eje y es horizontal. La Fig. E1.15.c muestra los mismos ejes vistos en un plano de perfil.

A su vez, las Figuras E1.15.d y e muestran las fuerzas dadas y las reacciones correspondientes. Las fuerzas de fricción H xy H y, que actúan en el plano de contacto de ambos cuerpos (tangenciales), corresponden a las componentes de la fuerza de fricción total H, también tangencial, pero de dirección desconocida. La reacción normal N, de dirección z, se aprecia en el plano de perfil. Por cierto la reacción R total del plano sobre el bloque corresponde a la composición de las 3 componentes de reacción:

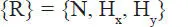
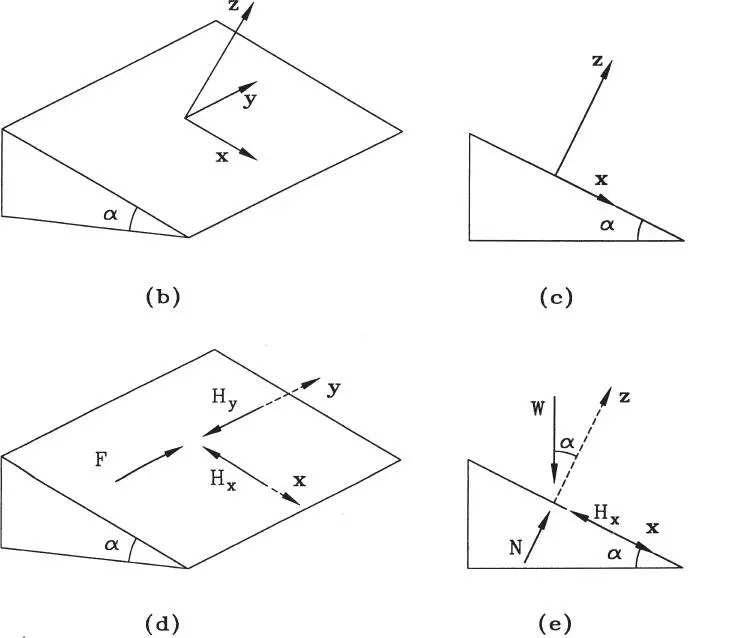
Figura E1.15

Las ecuaciones de equilibrio son muy simples, en efecto:

a) La fricción total H es la composición de las fuerzas tangenciales H xy H y, como muestra la Fig. E1.15.f. Como el triángulo OAB es rectángulo, se tiene:

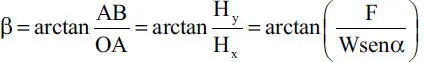
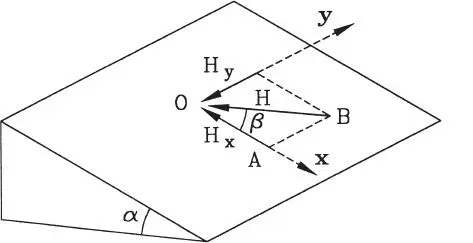
Figura E1.15.f