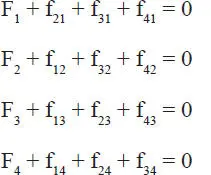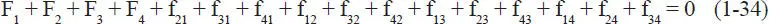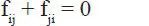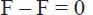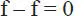Rafael Riddell Carvajal - Fundamentos de ingeniería estructural para estudiantes de arquitectura

Análogamente, si se considera el sistema constituido por el cilindro 2 de la Fig. 1.33.c, las fuerzas externas a él son su propio peso W 2, la acción N que le ejerce el cilindro 1, y P y Q reacciones del piso y la pared que lo sostienen (Fig. 1.34.b). Finalmente, si el sistema considerado incluye ambos cilindros, como ilustra la Fig. 1.34.c, las fuerzas externas son W 1, W 2, P, Q, y R; notar que en este subsistema no debe incluirse la interacción interna N por ser precisamente una fuerza interna del sistema.

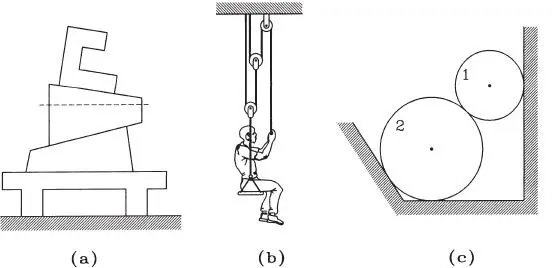
Figura 1.33Sistemas de varios componentes

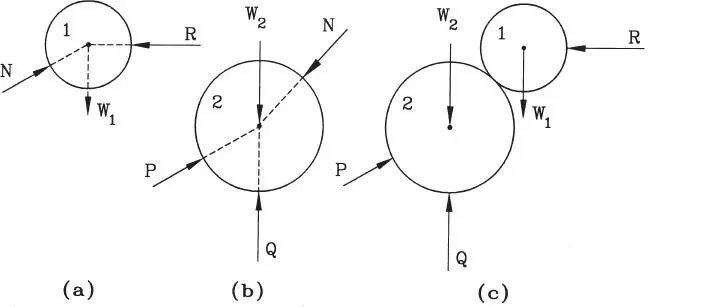
Figura 1.34Posibles subsistemas del sistema de la Fig. 1.33.c

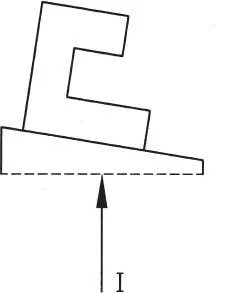
Figura 1.35Subsistema del sistema de la Fig. 1.33.a

Naturalmente el sistema a considerar no tiene por qué limitarse a incluir cuerpos completos. Por ejemplo, podría ser de interés analizar la porción sobre la línea segmentada de la Fig. 1.33.a, lo que equivale a seccionar la cuña correspondiente mediante un plano horizontal. Como muestra la Fig. 1.35, este tipo de análisis puede ser requerido si se desea determinar la fuerza interna I global que se transmite a través del plano o sección interna. La evaluación de esfuerzos internos en elementos estructurales es un tema de gran relevancia que se estudiará en detalle en el Capítulo 2.

1.6.2 Condiciones de Equilibrio

Es condición necesaria y suficiente para el equilibrio de un sistema de partículas , que cada una de las partículas que lo constituyen esté individualmente en equilibrio . Esta es una verdad evidente que no necesita demostración, sin embargo desde el punto de vista operativo resulta impracticable plantear las condiciones de equilibrio para las infinitas partículas de un sistema. Por ello, resulta conveniente indagar sobre condiciones más generales que permitan sacar conclusiones sobre el equilibrio del sistema.

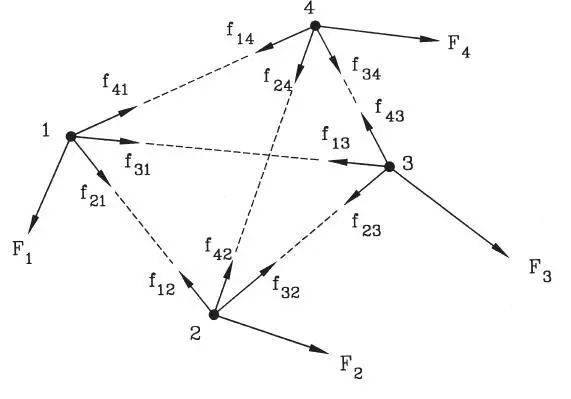
Figura 1.36Sistema de partículas

Considérese para ello el sistema de cuatro partículas sin peso de la Fig. 1.36. En particular, sobre la partícula 1 actúa una fuerza externa designada por F 1y fuerzas internas de interacción f 21, f 31y f 41que le ejercen las partículas 2, 3 y 4 respectivamente. Si cada partícula está en equilibrio, se pueden escribir 4 ecuaciones simbólicas (Ec. 1-29):

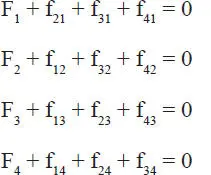
recordando que estas ecuaciones no son algebraicas porque las cantidades involucradas son fuerzas que aparte de magnitud tienen dirección y sentido. Sumando las 4 ecuaciones anteriores se tiene:

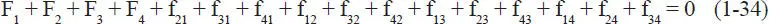
Por ser las fuerzas de interacción entre dos partículas iguales en dirección y magnitud, pero de sentido contrario, se tiene que f ij= -f jiluego

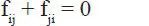
es decir, todas ellas se anulan en pares respectivos, luego la Ec. 1-34 queda

ecuación simbólica que indica que es condición necesaria para el equilibrio de un sistema de partículas que la suma de fuerzas externas sea nula , insistiendo nuevamente que dicha suma es vectorial y no algebraica. Por otra parte, si la Ec. 1-35 se introduce en la Ec. 1-34, se concluye que es condición necesaria para el equilibrio de un sistema de partículas que la suma vectorial de las fuerzas internas sea nula .

Como se discutió en la Sección 1.5, el que las condiciones anteriores sean solamente necesarias significa que si el sistema está en equilibrio ellas se cumplen, pero, el que ellas se cumplan no garantiza el equilibrio, es decir ellas no son condiciones suficientes para el equilibrio.

Un ejemplo simple, que ilustra el carácter de estas condiciones, es el siguiente. Considérese dos partículas 1 y 2 sin masa unidas por un elástico, como muestra la Fig. 1.37, a las que se aplican fuerzas externas F iguales y de sentido opuesto, que producen reacciones internas f en el elástico; si las fuerzas f no son capaces de equilibrar a cada una de las partículas, es decir f

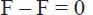
y también que la suma de fuerzas internas es nula

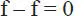
Similarmente, pueden enunciarse condiciones necesarias de equilibrio en términos de la suma de momentos de las fuerzas internas y externas del sistema de partículas. Sin embargo, como el concepto de momento se presentará recién en la Sección 1.8 esta discusión se omitirá aquí.

Finalmente, es importante destacar que si el sistema de partículas es rígido, es decir, la unión entre ellas es indeformable, las condiciones que antes eran sólo necesarias pasan a ser también suficientes, de manera que las ecuaciones de equilibrio globales garantizan el equilibrio. Es lo que ocurriría si en vez de un elástico en la Fig. 1.37 hubiese una barra rígida entre las partículas 1 y 2.

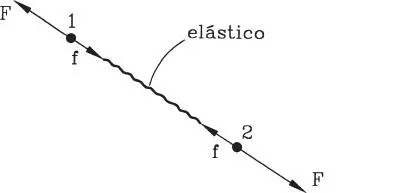
Figura 1.37Partículas unidas por elástico

1.7 Roce

Se denomina roce o fricción a la oposición natural al deslizamiento relativo entre dos objetos en contacto. La cualidad de las superficies que desarrollan este fenómeno se denomina rugosidad o aspereza. Por el contrario, las superficies incapaces de desarrollar fricción se llaman lisas , como ya se ha mencionado antes en algunos ejemplos. En realidad siempre existe roce, de manera que la idealización de contacto liso corresponde a un modelo simplificado que puede ser útil en muchos casos.

Las fuerzas de roce permiten realizar acciones tan simples como caminar, lo que sería imposible sobre una superficie perfectamente lisa. Sin la fricción tampoco podrían moverse los vehículos, los clavos no permanecerían en su sitio, no existirían las dunas de arena, los lápices se escaparían de nuestros dedos, los objetos se caerían de las repisas, etc. Por otra parte, en muchas aplicaciones el roce tiene efectos indeseados que es necesario minimizar, por ejemplo, en las máquinas origina desgaste de las superficies en contacto y pérdida de energía, ya que las fuerzas opuestas al movimiento deben contrarrestarse permanentemente. Por ello en esos casos se utilizan superficies cuidadosamente pulimentadas, sistemas de rodamientos, y lubricación.