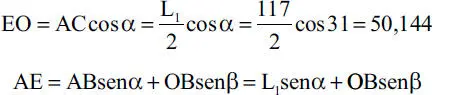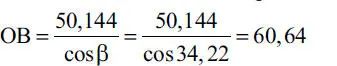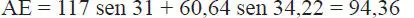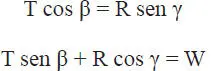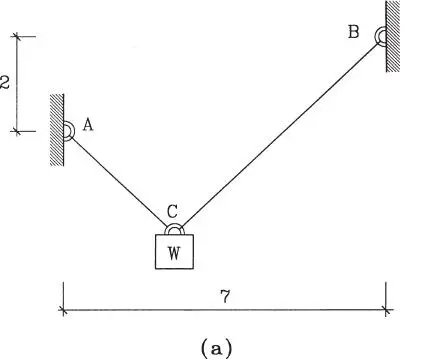
Figura E1.11.a
Solución:En este caso la posición de equilibrio no corresponde a aquella de la Fig. E1.9.a porque la armella C se desplazará sobre la cuerda hasta que el bloque adopte la posición más baja posible. Pero esta posición no es conocida a priori y debe ser calculada. Situaciones como ésta ocurren con cierta frecuencia en los problemas de estática, y se dice que en ellas la configuración de equilibrio , o geometría del estado de equilibrio , no es conocida de antemano. Entonces la solución del problema involucra el cálculo de incógnitas geométricas, además de las típicas fuerzas incógnitas. En la Fig. E1.11.b se plantea entonces la configuración de equilibrio en términos de las incógnitas x e y, mientras en la Fig. E1.11.c se muestran las fuerzas del modelo de partícula en el punto C.
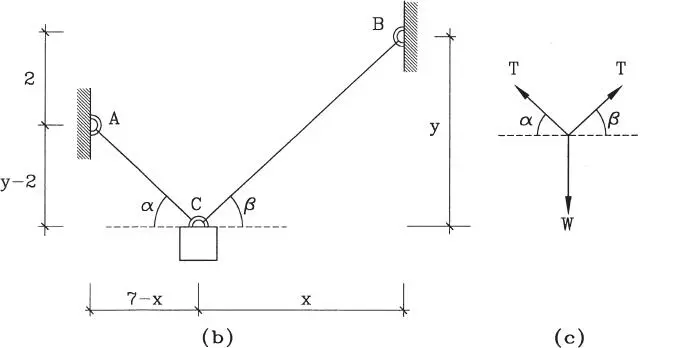
Figura E1.11.b y c
De estas dos figuras se concluye que el problema tiene 3 incógnitas: T, x e y (notar que los ángulos α y β no son incógnitas adicionales, ya que si se conocieran x e y, ellos quedarían perfectamente determinados). Para poder resolver el problema se requieren entonces 3 ecuaciones, estas son:
i) La longitud total de la cuerda es la misma del Ejemplo 1.9, es decir según la Fig. E1.9.a:
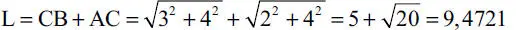
Pero, de la Fig. E1.11.b:
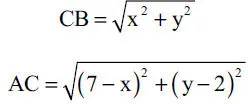
luego
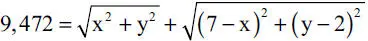
ii) Equilibrio de componentes horizontales en la Fig. E1.11.c:
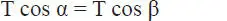
lo que implica que α=β y por lo tanto puede plantearse otra ecuación en términos de x e y, por ejemplo utilizando tan α = tan β se tiene
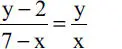
de donde puede despejarse x como
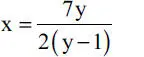
iii) Equilibrio de componentes verticales en la Fig.E1.11.c:
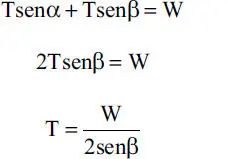
que entregará el valor de T una vez calculado β a partir de x e y.
Las ecuaciones derivadas en i e ii permiten calcular x e y. En efecto, introduciendo la segunda en la primera se obtiene una ecuación para y:

Puede entonces determinarse el ángulo β de:
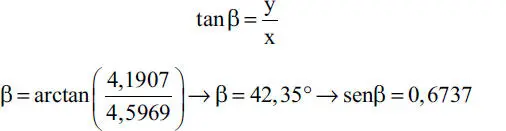
y finalmente
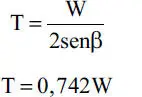
Ejemplo 1.12
Determinar analíticamente las fuerzas R y T del problema de la Fig. 1.32 si W=100 kg, L 1=117 cm, L 2=92 cm, α=31º, y h=112 cm.
Solución:Cabe primero destacar que la solución gráfica que muestra la Fig. 1.32.b es extremadamente simple, ya que basta con adoptar una escala para representar la dimensión de la fuerza W y las direcciones de las fuerzas R y T se toman paralelamente de las direcciones que ellas tienen en la Fig. 1.32.a. Los valores de R y T se leen a la misma escala en la Fig. 1.32.b. La solución analítica que sigue, en cambio, es más elaborada ya que requiere determinar previamente los ángulos β y γ (Fig. E1.12) haciendo uso de las condiciones geométricas del problema. Para ello considérese la Fig. E1.12, donde se tiene que:
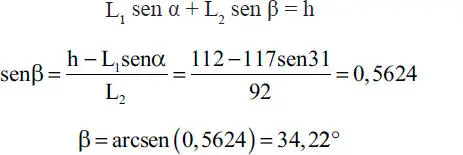
Por otra parte, tan γ 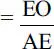 con
con
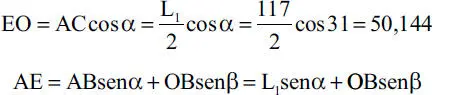
Pero, OB cos β = BC cos α = AC cos α = 50,144, luego
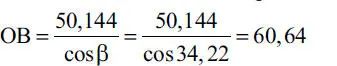
Reemplazando en la expresión de AE se tiene
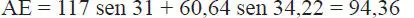
luego
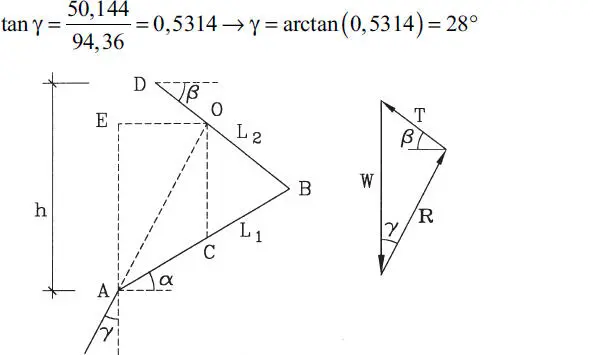
Figura E1.12
Finalmente, utilizando el polígono de fuerzas en la Fig. E1.12, haciendo equilibrio de fuerzas en direcciones horizontal y vertical respectivamente, se tiene:
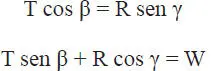
Reemplazando la primera ecuación en la segunda queda:

1.6 Equilibrio de un Sistema de Partículas
1.6.1 Noción de Sistema
Cualquier sistema que contenga más de una partícula es un sistema de partículas. Lo más común es que los sistemas estén constituidos por diversos cuerpos, los que a su vez pueden tener distintas partes conformadas por infinitas partículas. Lo importante para el análisis del equilibrio es tener claro cuál es el sistema que se está considerando, al que se aisla arbitrariamente para centrar la atención en él. La Fig. 1.33 muestra diversos sistemas en que el lector puede ejercitarse identificando cuántas partes los componen.
A continuación se analizará en detalle el sistema de la Fig. 1.33.c. Supóngase que interesa analizar el equilibrio del cilindro 1; esta parte, o subsistema del conjunto total, pasa a ser el sistema u objeto en que se centra el interés. Para el análisis del sistema seleccionado se prepara el llamado diagrama de cuerpo libre , en el cual se presenta el cuerpo de interés aislado de los otros cuerpos que interactúan con él. La interacción se representa por medio de las fuerzas que los cuerpos externos al sistema ejercen sobre el cuerpo de interés. Como se aprecia en la Fig. 1.34.a, sobre el cilindro 1 actúan las fuerzas externas siguientes: N, reacción del cilindro 2 sobre el cilindro 1, R, reacción de la pared vertical sobre el cilindro 1, y su propio peso W 1. Se define entonces como fuerza externa de un sistema aquella que es ejercida por una partícula ajena al sistema, mientras que una fuerza que actúa sobre una partícula de un sistema es interna cuando es ejercida por otra partícula del mismo sistema. En la Fig. 1.34.a no aparece ninguna fuerza interna, porque no se han representado las fuerzas de contacto entre las infinitas partículas que constituyen la materia del cilindro 1. Cabe destacar también que el peso W 1es una fuerza externa porque es ejercida por la atracción gravitacional de la Tierra, cuerpo externo al cilindro 1. Ciertamente, para estudiar el equilibrio del cilindro 1, se le puede modelar como una partícula hipotética ubicada en su centro de gravedad, donde concurren las tres fuerzas que actúan sobre él.
Читать дальше



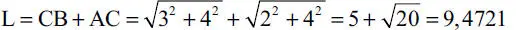
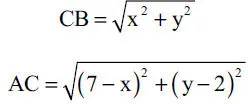
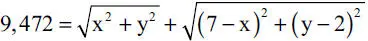
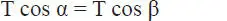
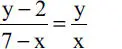
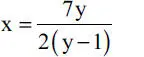
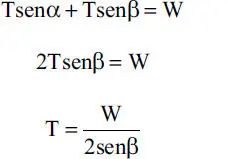

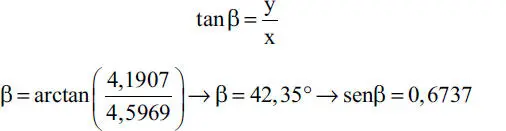
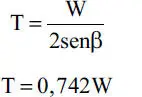
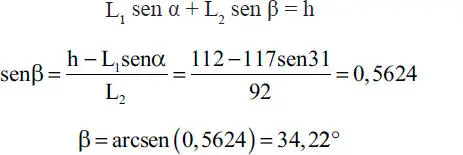
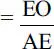 con
con