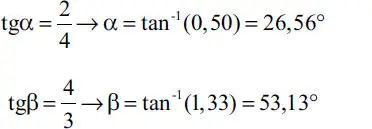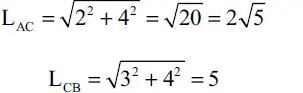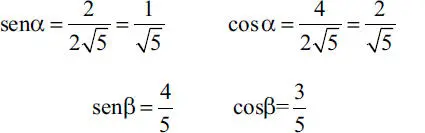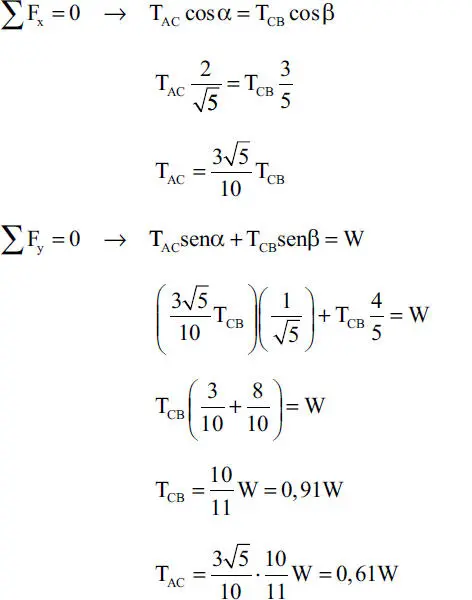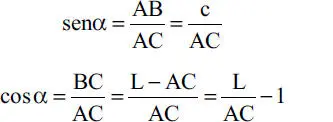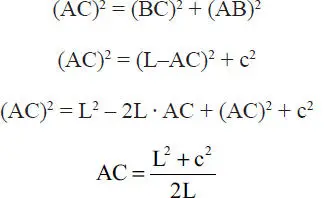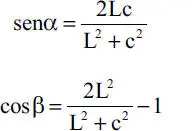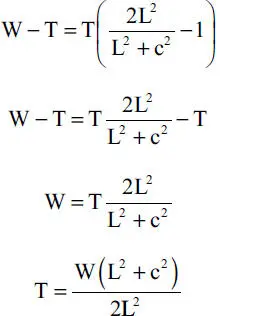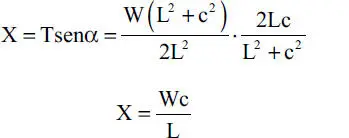Rafael Riddell Carvajal - Fundamentos de ingeniería estructural para estudiantes de arquitectura

Un ejemplo simple de lo anterior es el estudio del equilibrio de la barra homogénea de largo L 1de la Fig. 1.32.a, que se apoya en el piso en su extremo A, formando ángulo α con la horizontal, y cuelga de un hilo de largo L 2atado a su extremo B. Considerando que el peso W de la barra puede suponerse actuando verticalmente en su punto medio C, y que la dirección del hilo es conocida, y por tanto conocida la línea de acción de la fuerza T en el hilo, el equilibrio requiere forzosamente que la reacción R del piso sobre la barra pase por el punto O intersección de W y T. El cálculo de las magnitudes de R y T es muy simple, pudiendo por ejemplo obtenerse del polígono de fuerzas (triángulo) como muestra la Fig. 1.32.b. La solución analítica de este problema se presenta en el Ejemplo 1.12 al término de esta Sección.

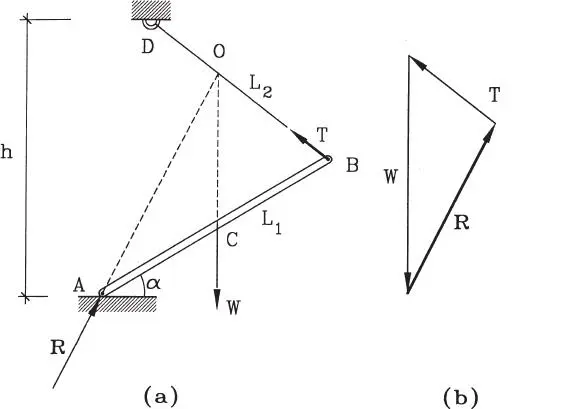
Figura 1.32Barra de dimensiones finitas modelada como partícula

Ejemplo 1.9

Un bloque de peso W cuelga de dos cuerdas livianas como se muestra en la Fig. E1.9.a. Determinar las fuerzas que deben realizar las cuerdas.

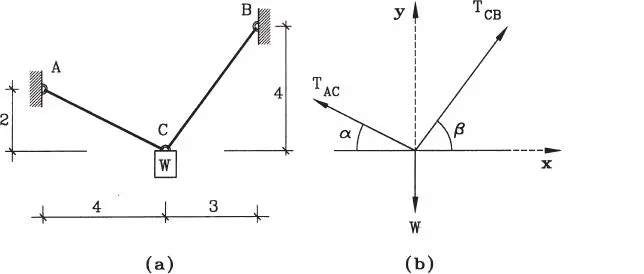
Figura E1.9

Solución:Corresponde a un caso de tres fuerzas concurrentes en el punto C, el que puede modelarse como una partícula en la forma que muestra la Fig. E1.9.b. En esta figura aparecen los siguientes elementos: la fuerza conocida W, las fuerzas incógnitas T ACy T CB, y los ángulos α y β. Los valores de los ángulos no han sido dados directamente, pero quedan perfectamente determinados por las dimensiones geométricas indicadas en la Fig. E1.9.a. En efecto, en base a las pendientes de las cuerdas pueden determinarse los ángulos:

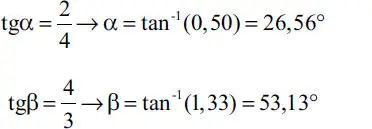
Alternativamente, sin calcular directamente α y β, se pueden obtener las funciones trigonométricas que intervendrán en las ecuaciones de equilibrio. Para ello se requiere previamente determinar las longitudes de las cuerdas:

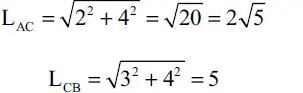
con lo cual

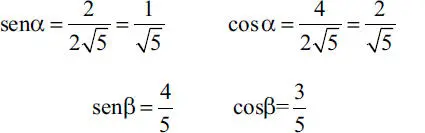
Aplicando las ecuaciones equilibrio en términos de las componentes según direcciones x e y (Ecs. 1-30 ó 1-31) se tiene:

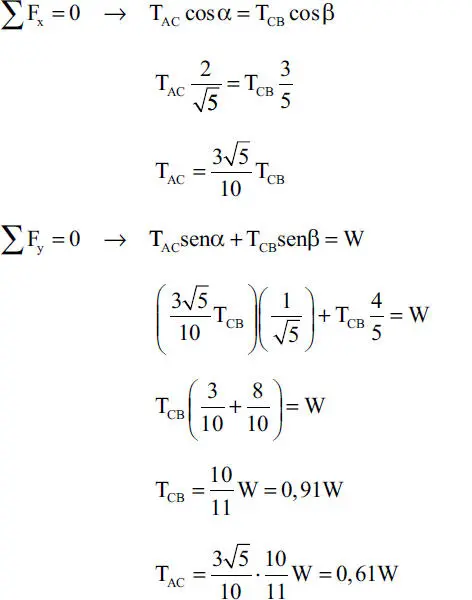
Ejemplo 1.10

Un hilo liviano de largo L está unido a dos puntos A y B a la misma altura y a distancia c. Por el hilo puede deslizar libremente un anillo pequeño de peso W. Determinar la fuerza horizontal que hay que aplicar al anillo para que se mantenga en equilibrio verticalmente bajo el punto B. Calcular la fuerza que desarrolla el hilo. Suponer que las fuerzas sobre el anillo son concurrentes.

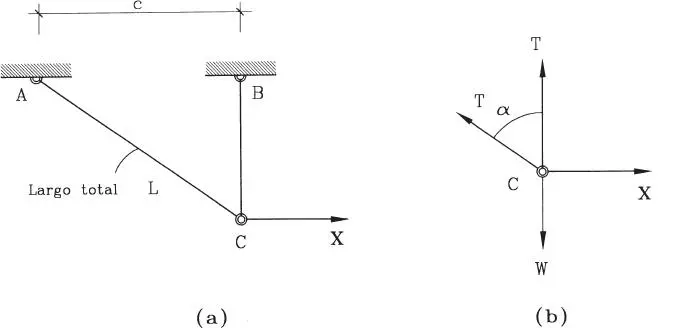
Figura E1.10

Solución:El problema planteado se muestra en la Fig. E1.10.a. Como el anillo puede correr libremente por el hilo, si no se aplicara la fuerza horizontal indicada (X=0) el equilibrio se lograría con el anillo ubicado sobre el eje de simetría entre A y B (simetral de AB). Dependiendo de la magnitud de la fuerza X se puede lograr el equilibrio en distintas posiciones, de manera que el caso planteado es una de las infinitas situaciones posibles. Como se trata de un hilo continuo, sin fricción en su contacto con el anillo, la fuerza T en el hilo es constante en toda su longitud, de manera que la acción del hilo sobre el anillo es como se muestra en la Fig. E1.10.b.

En la Fig. E1.10.b aparecen el peso conocido W, las fuerzas incógnitas T y X, y el ángulo α que es un parámetro geométrico que debe determinarse con los datos L y c, y de la condición de que el triángulo ABC es rectángulo. Conocido α, T y X pueden obtenerse de las dos ecuaciones de equilibrio según componentes horizontales y verticales, de manera análoga al ejemplo anterior. En este caso, sin embargo, se aprovechará de ilustrar otro método: el uso del polígono de fuerzas.

Recordando que la condición de equilibrio de la partícula es que el polígono de fuerzas sea cerrado, pueden construirse varios polígonos dependiendo del orden en que se tomen las fuerzas. De hecho, como en este caso hay 4 fuerzas, existen 24 posibilidades distintas de escoger su secuencia, aunque varias de ellas repiten las mismas formas poligonales. Las Figs. E1.10.c, d, e y f muestran cuatro de estas posibilidades, todas construidas con el punto O como punto de inicio; algunas fuerzas se han desplazado ligeramente para apreciar mejor la secuencia de construcción. Notar, sin embargo, que la construcción sólo es posible si T

Figura E1.10

Todos los polígonos de fuerzas conducen al triángulo de la Fig. E1.10.g, al cual puede aplicarse el Teorema de Lamy, o simplemente las relaciones obvias en proyecciones horizontal y vertical respectivamente:

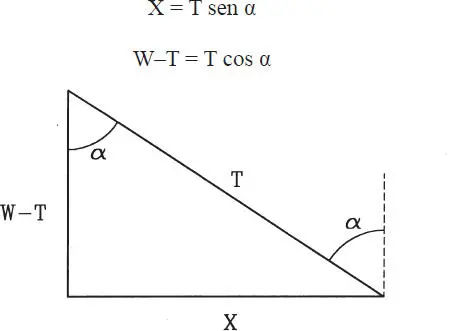
Figura E1.10.g

Considerando el triángulo rectángulo ABC de la Fig. E1.10.a se tiene:

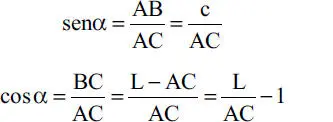
falta entonces determinar AC, lo que puede hacerse aplicando el Teorema de Pitágoras al triángulo ABC:

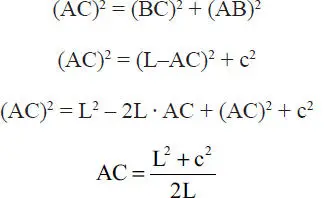
entonces:

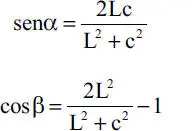
Reemplazando la ecuación anterior en la segunda ecuación de equilibrio se tiene:

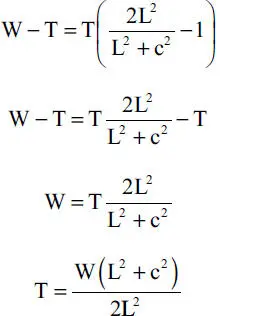
y reemplazando el resultado anterior en el primera ecuación de equilibrio se tiene:

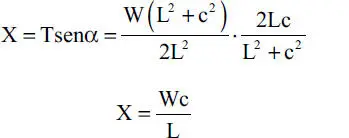
Ejemplo 1.11

Considérese el mismo Ejemplo 1.9 pero con la diferencia que las dos cuerdas independientes se han reemplazado por una cuerda continua de igual largo total. Suponiendo contacto liso entre la cuerda y la armella del bloque, calcular la fuerza de tracción a que queda sometida la cuerda.