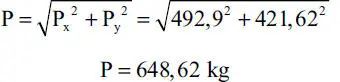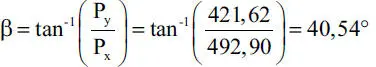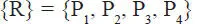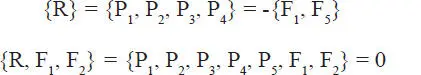Rafael Riddell Carvajal - Fundamentos de ingeniería estructural para estudiantes de arquitectura

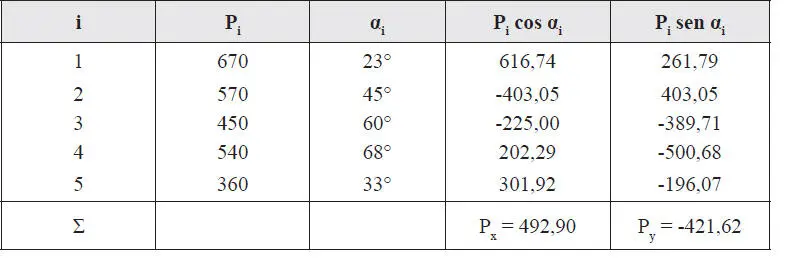
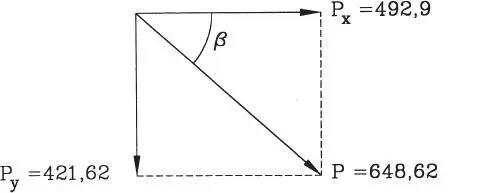
Figura E1.8.b

La suma de las proyecciones de las fuerzas sobre el eje x es la componente P xde la resultante, y análogamente P ypara el eje y. La resultante P, según la Ec. 1-23, tiene magnitud (Fig. E1.8.b):

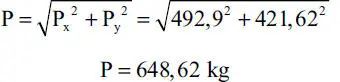
y su dirección queda dada por el ángulo β:

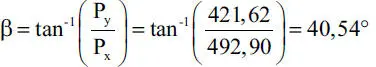
Notar que en la fórmula anterior se usó el valor absoluto de P yya que no se está utilizando el signo trigonométrico del ángulo β sino sólo su magnitud.

1.4.5 El Polígono Funicular

El procedimiento indicado en la Sección 1.4.2 para determinar la resultante de un sistema de fuerzas no concurrentes (Fig. 1.17), que consiste en la aplicación sucesiva de las leyes de transmisibilidad y del paralelogramo, puede reemplazarse por una construcción más conveniente, el polígono funicular, que también es aplicable al caso de un sistema de fuerzas paralelas. Además de ser una solución alternativa para los casos señalados, la mayor importancia de esta construcción radica en que permite profundizar algunos aspectos conceptuales del trabajo con sistemas de fuerzas, y en que ayudará a comprender el funcionamiento de una forma estructural muy notable en la historia de la arquitectura: el arco.

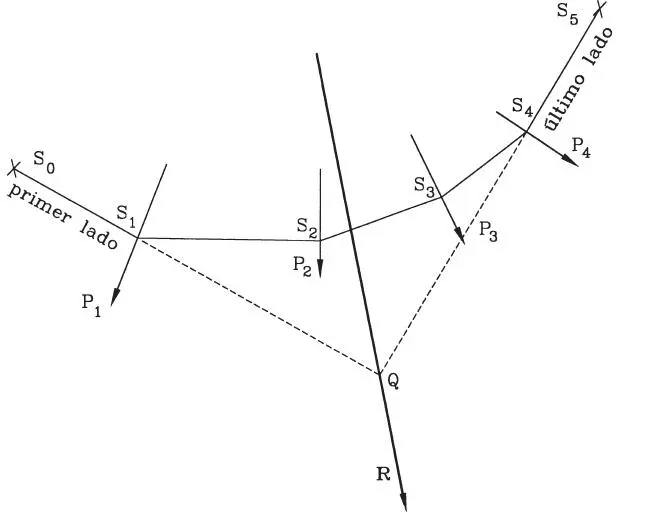
Figura 1.25.aPolígono Funicular

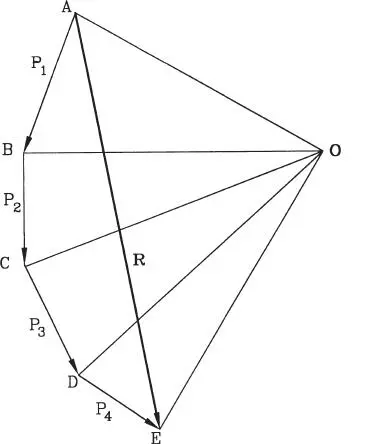
Figura 1.25.bPolígono de Fuerzas

Sea un sistema de fuerzas coplanares que actúan sobre un cuerpo rígido, tales como P 1, P 2, P 3y P 4en la Fig. 1.25.a. Las etapas de la construcción del polígono funicular son las siguientes:

a) Primero se construye el polígono de fuerzas, ABCDE en la Fig. 1.25.b, con el cual se determina la magnitud y dirección de la resultante R, pero no se conoce la posición precisa de su línea de acción.

b) Se escoge un punto arbitrario en el plano, tal como el punto O en la Fig. 1.25.b, que se denomina foco o polo. Desde el foco se trazan los rayos OA, OB, OC, OD, y OE a los extremos de las fuerzas P 1a P 4.

c) Se escoge arbitrariamente un punto de arranque , a partir del cual se comenzará a construir el polígono funicular. Este es el punto S oen la Fig. 1.25.a.

d) Pasando por S ose traza una recta paralela al rayo OA, hasta interceptar la fuerza P 1en el punto S 1; la recta trazada constituye el primer lado del polígono funicular. Pasando por S 1se traza una recta paralela al rayo OB, hasta interceptar la fuerza P 2; la recta S 1S 2constituye el segundo lado del polígono funicular. Y así, sucesivamente, trazando paralelas a OC, OD y OE se obtienen los lados S 2S 3, S 3S 4, y a partir de S 4el último lado del polígono funicular.

e) El punto Q, intersección de la prolongación del primer y del último lado del polígono funicular, es un punto de la línea de acción de la resultante R, quedando ésta totalmente determinada. Se tiene entonces que

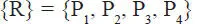
La calificación de “funicular” dada al polígono se debe a que tiene la forma que adoptaría un hilo sin peso, sujeto en sus extremos (puntos S oy S 5), al ser sometido a las fuerzas P 1, P 2, P 3y P 4actuando en los puntos S 1, S 2, S 3y S 4. Claramente dicho hilo se encontraría sometido a un esfuerzo de tracción en toda su longitud.

La analogía con el hilo facilitará explicar el fundamento de la construcción anterior. Para ello, se reconstruirá la Fig. 1.25 indagando sobre el equilibrio parcial de cada una de las fuerzas P idadas. Observando el polígono de fuerzas de la Fig. 1.26.b, y recordando que el punto O fue arbitrariamente elegido, se puede pensar que los rayos BO y OA(con sentido de B hacia O y de O hacia A) representan dos fuerzas arbitrarias F 2y F 1respectivamente que tienen la propiedad de equilibrar a la fuerza P 1; esto último porque el polígono OABO de las 3 fuerzas P 1, F 1y F 2es cerrado, es decir su resultante es nula. Puede pensarse entonces que el primer y segundo lado del polígono de la Fig. 1.26.a corresponden a fuerzas de tracción F 1y F 2en el hilo que equilibran a la fuerza P 1. Análogamente, la fuerza P 2en la Fig. 1.26.b está en equilibrio con las fuerzas arbitrarias F 3(con sentido de C hacia O) y F 2(con sentido de O hacia B), ya que el polígono OBCO es cerrado; las paralelas a OB y CO, es decir los lados segundo y tercero del polígono funicular de la Fig. 1.26.a corresponden a las fuerzas de tracción F 2y F 3en el hilo necesarias para equilibrar a la fuerza P 2. Así, sucesivamente, las fuerzas F 3y F 4equilibran a P 3, y F 4y F 5equilibran a P 4. Ahora bien, observando la Fig. 1.26.a, se aprecia que la fuerza F 2, que participa en el equilibrio de P 1, y la fuerza F 2, que participa en el equilibrio de P 2, se autoequilibran, ya que constituyen el segundo lado, o hilo continuo, del funicular; análogamente ocurre con las fuerzas F 3asociadas al tercer lado y F 4asociadas al cuarto lado.

En resumen, el primer tramo del hilo ejerce una fuerza F 1, que es la fuerza que debería realizar una persona que sostuviera el hilo desde el punto S o, y el último tramo del hilo ejerce una fuerza F 5, que habría que ejercer externamente para sostenerlo desde el punto S 5. Por supuesto si F 1y F 5equilibran al conjunto de fuerzas P 1, P 2, P 3y P 4, ellas equilibran a su resultante R, y por lo tanto R pasa por el punto de intersección de las líneas de acción de F 1y F 5; tal equilibrio también queda explícito en el polígono de fuerzas (Fig. 1.26.b), donde F 1, R y F 5constituyen un polígono cerrado (OAEO), o sea,

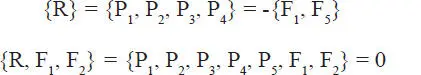
En los lados 2 o, 3 oy 4 oel hilo experimenta esfuerzos internos de tracción de magnitud F 2, F 3y F 4respectivamente.

Como la elección de la ubicación del foco del polígono de fuerzas es arbitraria, se pueden trazar infinitos polígonos funiculares distintos para un mismo sistema de fuerzas. El hecho de que la intersección del primer y último lado ocurra siempre sobre la misma línea recta constituye una propiedad notable. En geometría, a un conjunto de puntos que satisfacen una misma condición se le denomina lugar geométrico ; en este caso, la propiedad señalada puede expresarse diciendo que “el lugar geométrico de los puntos de intersección de los primeros y últimos lados de los infinitos polígonos funiculares que pueden trazarse para un sistema de fuerzas dado, es una línea recta, la que corresponde a la línea de acción de la resultante del sistema de fuerzas”.