Rafael Riddell Carvajal - Fundamentos de ingeniería estructural para estudiantes de arquitectura

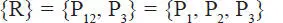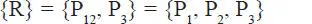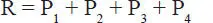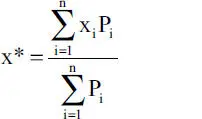
Figura 1.14

1.4.2 Composición de Fuerzas

La operación de composición de fuerzas corresponde a lo que ordinariamente se llama realizar la “suma” de las fuerzas. La palabra composición, sin embargo, enfatiza que tal operación no es una simple suma, ya que en ella intervienen simultáneamente las tres propiedades de las fuerzas: magnitud, dirección, y sentido. La composición puede realizarse en forma analítica utilizando el álgebra vectorial, pero ello no se hará aquí, ya que tales conocimientos no son requisito para los lectores de este texto; en cambio, se privilegiará una presentación geométrica, que tiene la ventaja adicional de mantenerse más próxima a la realidad física del problema. Un método analítico simple, que sólo requiere el uso de la trigonometría, se verá más adelante en el Ejemplo 1.8.

Sean P 1y P 2(Fig. 1.15.a) dos fuerzas concurrentes en el punto O, su composición se realiza aplicando la Ley del Paralelogramo que establece que la resultante de dos fuerzas concurrentes es la diagonal del paralelogramo formado por ellas . Notar que dos fuerzas concurrentes son forzosamente coplanares. La construcción geométrica se realiza en la forma indicada en la Fig. 1.15.b: por el extremo A 1de la fuerza P 1se traza una paralela a la fuerza P 2, y por el extremo A 2de la fuerza P 2se traza una paralela a la fuerza P 1, formándose el paralelogramo OA 1BA 2. La fuerza R aplicada en O, de magnitud igual a la diagonal del paralelogramo, de dirección OB, y sentido de O a B, es la resultante de P 1y P 2, es decir su efecto es enteramente equivalente a la acción conjunta de P 1y P 2. Se dice entonces que R es estáticamente equivalente a P 1y P 2y se escribe simbólicamente:

La extensión del procedimiento anterior al caso de varias fuerzas coplanares concurrentes es trivial. Efectivamente, basta con proceder en forma sucesiva con pares de fuerzas. La Fig. 1.16.a muestra en un sistema dado de 3 fuerzas. En la Fig. 1.16.b se muestra la composición de P 1y P 2obteniéndose la resultante parcial P 12, y finalmente, en la Fig. 1.16.c se componen P 12con P 3obteniéndose la resultante final R. Se tiene entonces:

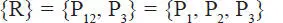
Naturalmente el punto O de la Fig. 1.16.c es coincidente con el punto O de la Fig. 1.16.a; la presentación en tres figuras separadas sólo ha tenido por objeto mostrar con mayor claridad las etapas de la construcción geométrica.

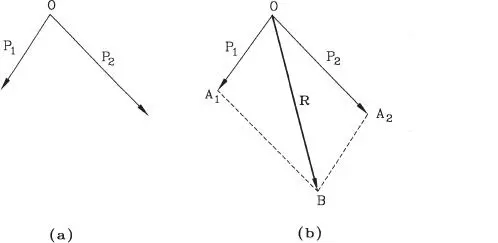
Figura 1.15Composición de fuerzas

Figura 1.16Composición de 3 fuerzas concurrentes

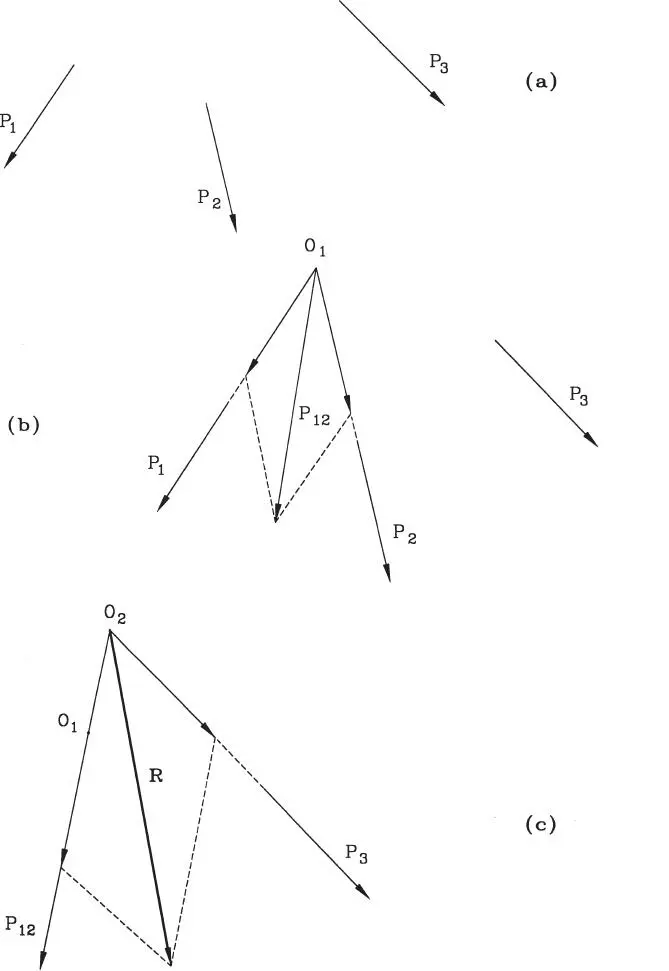
Figura 1.17Composición de fuerzas no concurrentes

En el caso de fuerzas coplanares no concurrentes a un punto, el procedimiento anterior puede aplicarse con ayuda del principio de transmisibilidad de las fuerzas. Sean tres fuerzas coplanares cualesquiera como P 1, P 2y P 3de la Fig. 1.17.a. Las fuerzas P 1y P 2pueden primero trasladarse a su punto de intersección O 1(Fig. 1.17.b), y construir allí el paralelogramo correspondiente para encontrar su resultante P 12. A continuación se componen las fuerzas P 12y P 3, trasladándolas a su punto de intersección O 2(Fig. 1.17.c), donde se construye su paralelogramo para determinar R, fuerza estáticamente equivalente al sistema original dado:

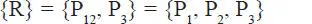
Las construcciones geométricas anteriores no son factibles si las fuerzas son paralelas. En tal caso se puede proceder mediante la construcción del Polígono Funicular , que se verá en la Sección 1.4.5, pero también es posible utilizar el concepto de centro de gravedad, como se describe a continuación. Sean varias fuerzas coplanares paralelas P 1, P 2, P 3y P 4, como ilustra la Fig. 1.18, y sean x 1, x 2, x 3, y x 4sus distancias a un origen de referencia O. La resultante de este sistema tiene magnitud R igual a la suma de las magnitudes de las fuerzas dadas:

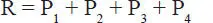
y su línea de acción pasa por el punto de coordenada x* tal que (Ec. 1-10):

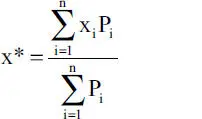
La regla anterior funciona incluso si algunas fuerzas tienen sentido contrario. El caso especial en que la suma algebraica de las magnitudes de las fuerzas es nula, i.e. x*=∞, se interpretará físicamente más adelante.

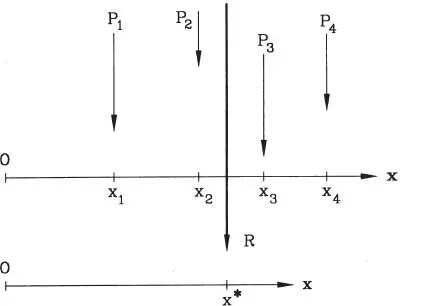
Figura 1.18Composición de fuerzas coplanares paralelas

1.4.3 El Polígono de Fuerzas

Una forma geométrica alternativa de encontrar la resultante de un sistema de fuerzas es construir el polígono de ellas, lo que se realiza copiando paralelamente las fuerzas una a continuación de la otra. Por ejemplo, considerando el sistema de fuerzas dado en la Fig. 1.16.a, el polígono de las fuerzas corresponde a la línea OABC de la Fig. 1.19.a y la fuerza resultante R es la que va desde el inicio de la primera fuerza al término de la última, es decir de O a C. Obviamente, para realizar la construcción del polígono de fuerzas es inmaterial el orden en que se copian las fuerzas, resultando siempre el mismo punto final para cualquiera de las combinaciones posibles.

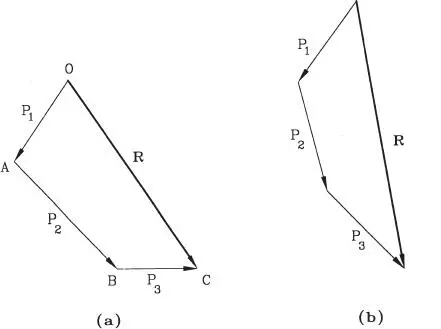
Figura 1.19Polígonos de fuerzas

Si el sistema de fuerzas es concurrente, como el de la Fig. 1.16.a, la resultante queda completamente determinada pues se conoce un punto de su línea de acción, el punto de concurrencia O. En el caso de un sistema de fuerzas no-concurrentes como el de la Fig. 1.17.a también se puede construir su polígono, como se muestra en la Fig. 1.19.b; ello permite encontrar la resultante en magnitud y dirección, pero no se conoce su línea de acción ya que no se dispone de un punto de ella. Para definir ese punto hay que realizar la construcción de la Fig. 1.17 o recurrir al polígono funicular que se presentará en la Sección 1.4.5.