Rafael Riddell Carvajal - Fundamentos de ingeniería estructural para estudiantes de arquitectura

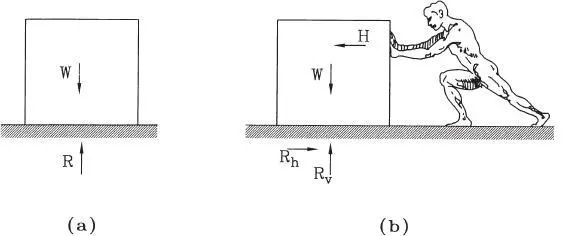
Figura 1.8Fuerzas reactivas

En la Fig. 1.8.b se observa el mismo bloque anterior al cual se ha aproximado un hombre a ejercer una fuerza horizontal H. Si el bloque se mantiene en reposo se deduce que no sólo hay restricción a su movimiento vertical, sino también a su desplazamiento horizontal hacia la izquierda. Como existen dos desplazamientos impedidos, se concluye la existencia de dos fuerzas reactivas asociadas a ellos R vvertical y R hhorizontal. Cabe notar además que la fuerza reactiva R hse genera en respuesta a la demanda H, es decir si ésta no estuviese presente, no existiría R h, porque no existiría posibilidad alguna de movimiento en dirección horizontal. Notar también que esta discusión es independiente del mecanismo físico que origina la fuerza R h; si el reposo se ha mantenido puede ser simplemente porque existe suficiente fricción en el contacto del bloque con el piso, o bien porque el bloque está clavado al piso.

1.3.3 Centro de Gravedad

A excepción de las partículas, en los cuerpos la masa (materia) está distribuida en la extensión de su volumen, por ello, el peso de un cuerpo está también repartido espacialmente.

Esta distribución del peso puede visualizarse considerando un cuerpo de forma simple, como por ejemplo el tablero rectangular de madera, de espesor constante, que muestra la Fig. 1.9.a. Suponiendo que el material es homogéneo , es decir que sus propiedades son las mismas en toda su extensión, cualquier porción de igual volumen tiene el mismo peso. Si imaginariamente se considera el tablero subdividido en 25 partes, como en la Fig. 1.9.a, cada parte pesa p=P/25, siendo P el peso total del tablero. Por cierto, puede pensarse en un número muy grande de partes, y cada parte pesará la fracción correspondiente del total, llegándose a una distribución uniforme muy fina del peso total.

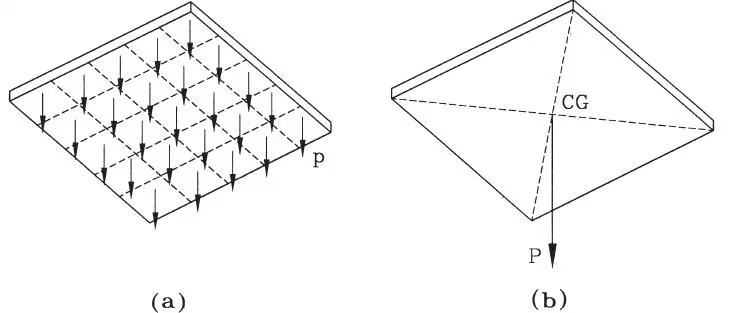
Figura 1.9Tablero de madera: a) peso distribuido, b) peso concentrado

Trabajar con la distribución real de la masa de un cuerpo exigiría considerar un número enorme de pequeñas fuerzas correspondientes a su peso distribuido. Ello sería muy complejo, aún para cuerpos de forma simple como el de la Fig. 1.9. Afortunadamente tal complejidad es innecesaria porque desde el punto de vista del equilibrio en todo cuerpo existe un punto, llamado centro de gravedad , en el cual puede suponerse actuando concentradamente su peso total, como se muestra en la Fig. 1.9.b para el ejemplo del tablero. Se dice entonces que la fuerza o peso total P de la Fig. 1.9.b es estáticamente equivalente a la distribución uniforme de pesos p de la Fig. 1.9.a.

El centro de gravedad no es un punto arbitrariamente definido sino un punto que efectivamente tiene una propiedad física muy especial. Por ejemplo, si se quiere equilibrar el tablero apoyándolo en un solo punto (en la punta de un clavo o de un dedo), el único punto que permitirá lograr el equilibrio es el centro de gravedad (CG). Es decir, físicamente, el CG es el “centro” de la masa, o como también podría decirse, es el punto “promedio” de la distribución espacial de la masa.

Esta condición de “centro” o “promedio” permite deducir que siempre que un cuerpo homogéneo tenga un eje de simetría el CG estará sobre dicho eje. Ello porque siempre un eje de simetría divide el cuerpo en dos partes iguales, o sea de igual forma y peso, por lo tanto el “centro” no puede estar a uno ni otro lado de la línea divisoria sino sobre ella. Esto permite localizar en forma inmediata el CG de formas geométricas simples, ya que si hay dos ejes de simetría el CG debe estar en su intersección. Naturalmente en el caso de volúmenes, siempre que exista un plano de simetría el CG estará sobre él. La Fig. 1.10 muestra los CG de varios cuerpos simples: rectángulo, círculo, anillo, barra, esfera. En la Tabla V.2 se presentan propiedades y centros de gravedad de cuerpos comunes.

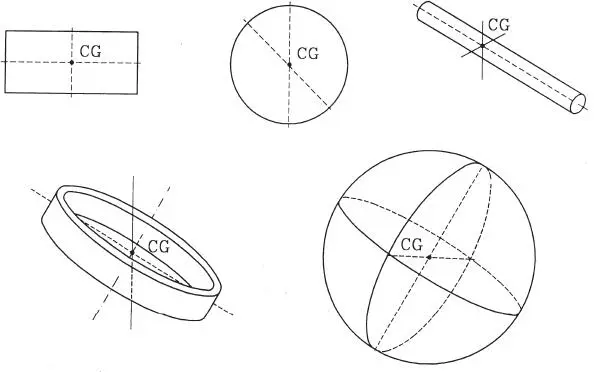
Figura 1.10Centros de gravedad de formas geométricas que presentan simetría

El caso del triángulo merece especial consideración. En un triángulo se definen las transversales de gravedad como las líneas que unen un vértice con el punto medio del lado opuesto. La Fig. 1.11.a muestra t c, la transversal de gravedad correspondiente al vértice C. Obviamente t cno es un eje de simetría, pero tiene la particular propiedad de dividir el triángulo en dos mitades iguales: de igual área y de igual peso si el material es homogéneo. De igual área porque por definición el punto D en la Fig. 1.11.a divide el lado AB en dos partes iguales de longitud c/2, luego las áreas de los triángulos ADC y BCD son ambas iguales a ch/4 (un medio de la base por la altura). Además las distancias de A y B a t cson iguales, y también deben serlo las distancias de los centros de gravedad de los triángulos ADC y DBC a t c, luego el CG del triángulo ABC debe estar sobre la línea t c. Si se traza cualquiera de las otras dos transversales de gravedad, t apor ejemplo, el CG debe estar en la intersección de t ay t c. Aún más, como lo anterior ocurre para cualquier par de transversales que se escoja (t acon t c, t bcon t c, o t acon t b) queda demostrado que las tres transversales de gravedad son concurrentes y que el CG es el punto de concurrencia (Fig. 1.11.b). Además, puede demostrarse que el CG intercepta a cada una de las transversales en segmentos cuyas longitudes están en la razón 1:2, es decir, la distancia de C a CG es el doble de la distancia de CG a D.

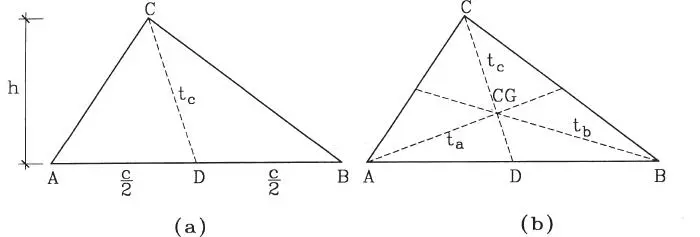
Figura 1.11Centro de gravedad de un triángulo

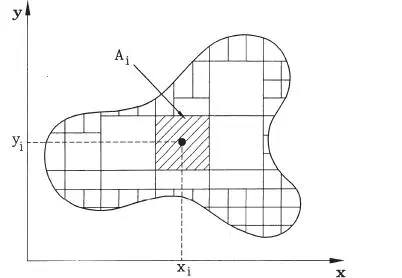
Figura 1.12Subdivisión discreta de un área plana

A continuación se considera la determinación de la ubicación del centro de gravedad para el caso de cuerpos planos homogéneos. Sea un cuerpo de forma cualquiera como el que se muestra en la Fig. 1.12, el cual se ha subdividido en un número n de áreas conocidas, en que el área del segmento i es A iy la posición del CG del segmento i está definida por las coordenadas x i, y i. En los bordes curvos la subdivisión deberá ser más fina, con el objeto de representar la forma del cuerpo de la manera más fiel posible mediante pequeños segmentos de formas regulares, como rectángulos, triángulos o trapecios. Las coordenadas del centro de gravedad del cuerpo se definen como:

Notar que las definiciones anteriores no son otra cosa que lo que normalmente se conoce como un promedio ponderado . En efecto, por ejemplo, lo que se denomina el promedio ponderado acumulado del rendimiento académico de un estudiante universitario tiene exactamente la misma definición: