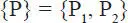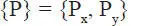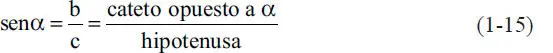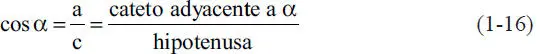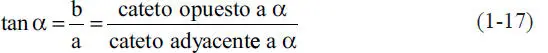Rafael Riddell Carvajal - Fundamentos de ingeniería estructural para estudiantes de arquitectura

Una situación de particular importancia es aquella en que el polígono de fuerzas es cerrado , es decir, la última fuerza termina exactamente en el punto de inicio de la primera, como se muestra en la Fig. 1.20. Este caso corresponde a un sistema de fuerzas con resultante nula , condición fundamental para el equilibrio de un sistema. Por esta razón, el polígono de fuerzas se utilizará más adelante como una herramienta geométrica fundamental para encontrar relaciones entre las fuerzas en un sistema en equilibrio.

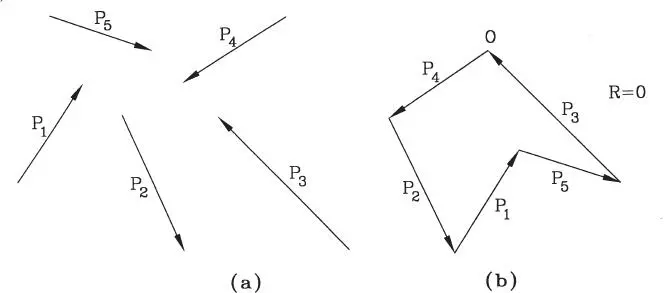
Figura 1.20Sistema con polígono de fuerzas cerrado

1.4.4 Descomposición de Fuerzas

Una fuerza puede descomponerse según dos direcciones cualesquiera aplicando la Ley del Paralelogramo en forma inversa. Dada la fuerza P y las direcciones 1 y 2 de la Fig. 1.21.a, las componentes P 1y P 2de P se obtienen completando el paralelogramo que tiene a P como diagonal, como se muestra en la Fig. 1.21.b. Obviamente se cumple que la fuerza P es estáticamente equivalente al conjunto de sus dos componentes, es decir:

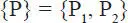
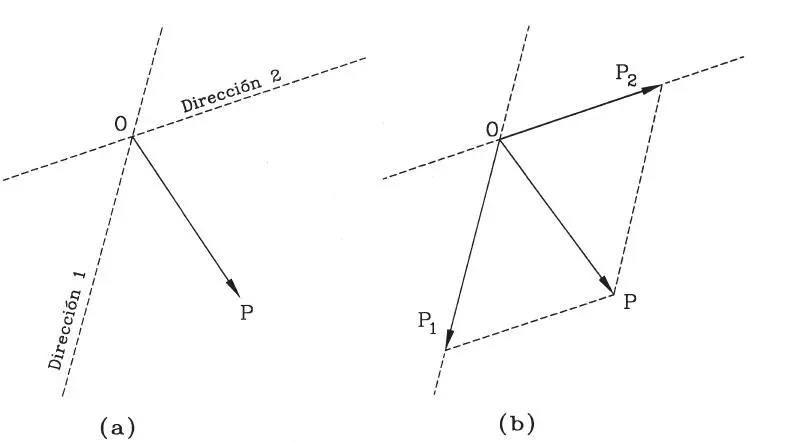
Figura 1.21Descomposición de una fuerza

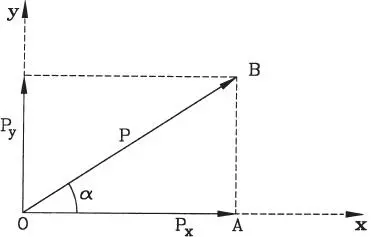
Figura 1.22Proyecciones ortogonales de una fuerza

Es muy usual y conveniente aplicar la descomposición utilizando dos direcciones perpendiculares entre sí, las que normalmente son referidas como ejes ortogonales , o sistema de ejes cartesiano . La Fig. 1.22 muestra una fuerza P que se ha descompuesto en sus componentes P xy P ysegún los ejes x e y. P xy P yse denominan también proyecciones de P sobre los ejes x e y respectivamente.

Obviamente:

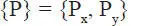
Las proyecciones ortogonales tienen la ventaja de permitir usar las funciones trigonométricas básicas, que en un triángulo rectángulo, como el de la Fig. 1.23, se definen como:

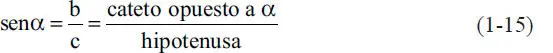
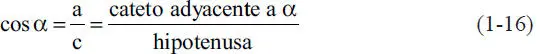
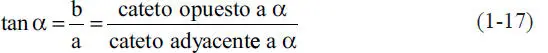
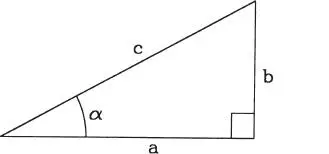
Figura 1.23Triángulo rectángulo

y sus inversas

Aplicando las Ecs. 1-15 y 1-16 a la Fig. 1.22 se tiene que:

y además, por ser OAB un triángulo rectángulo, en virtud del Teorema de Pitágoras se tiene que las magnitudes de P y de sus componentes cumplen con:

La Ec. 1-23 también puede demostrarse elevando al cuadrado y sumando las Ecs. 1-21 y 1-22 y utilizando la conocida identidad trigonométrica:

El Ejemplo 1.7 presenta una aplicación directa de la regla de descomposición a la solución gráfica de un problema de estática. El Ejemplo 1.8 presenta una metodología analítica general para la composición de un sistema de fuerzas concurrentes; el método se basa en descomponer primero todas las fuerzas en sus componentes, para después simplemente sumar estas últimas en forma algebraica.

Finalmente cabe mencionar que en el caso tridimensional, es decir una fuerza en el espacio, se utiliza un sistema de tres ejes coordenados ortogonales, sobre cada uno de los cuales se proyecta la fuerza para obtener las componentes P x, P y, P z(Fig. 1.24). Es claro que:

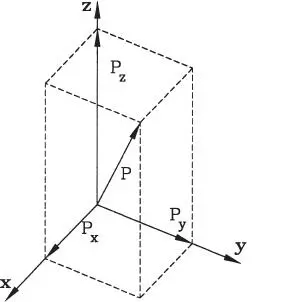
Figura 1.24Proyecciones ortogonales de una fuerza en el espacio

Ejemplo 1.7

Descomponer la fuerza P en las direcciones AC y BC para determinar los esfuerzos en las barras correspondientes. Para esta construcción se adopta una escala como la indicada en la figura en que una cierta longitud representa a tantas unidades de fuerza. Notar que la solución implica que la barra BC queda sometida a un esfuerzo interno de tracción, mientras la barra AC experimenta compresión.

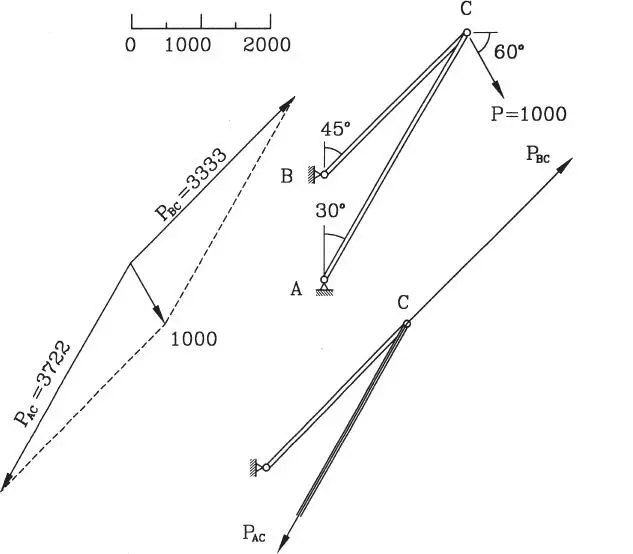
Figura E1.7

Ejemplo 1.8

Determinar la resultante del sistema de cinco fuerzas concurrentes que se muestra en la Fig. E1.8.a

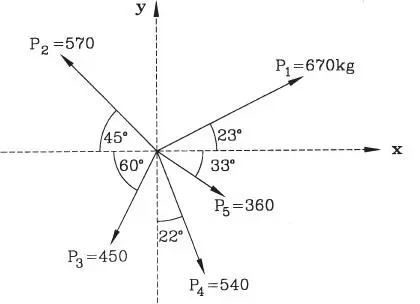
Figura E1.8.a

Solución:Los cálculos de las componentes x e y de cada una de las fuerzas se organizan en la Tabla siguiente. Notar que los signos negativos indican componentes que tienen el sentido negativo de los ejes de referencia.