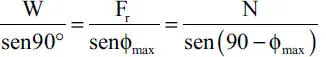Rafael Riddell Carvajal - Fundamentos de ingeniería estructural para estudiantes de arquitectura

El roce seco se refiere a la fuerza tangencial de contacto entre dos superficies secas que deslizan o tienden a deslizar una respecto a la otra. Se sabe que el roce seco se debe principalmente a la irregularidad de las superficies en contacto y a la atracción molecular de los materiales involucrados. El roce fluido se refiere a la fricción entre capas de un fluido, como ocurre entre un eje y su asiento lubricado con aceite. La lubricación tiene por objeto separar las superficies en contacto para minimizar el roce (Fig. 1.38). En algunos casos la lubricación no es deseada, como ocurre con el agua en el pavimento, pues reduce considerablemente las fuerzas de fricción; una medida para evitar la formación de la película de agua que separa el pavimento del neumático es el dibujo de éstos, el que obliga al agua a desplazarse hacia los intersticios del neumático, manteniendo el contacto efectivo de éste con el pavimento. Por otra parte, el polvo o arena sobre el pavimento puede causar un efecto similar al lubricante.

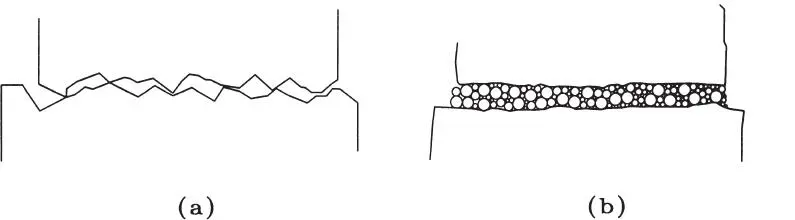
Figura 1.38Superficies en contacto ampliadas: a) terminación irregular en contacto seco, b) terminación suave lubricada

A su vez, debe distinguirse el roce estático , que se desarrolla entre superficies en reposo una con respecto a la otra, del roce cinético , que actúa entre superficies en movimiento relativo. A continuación se describirán las propiedades del roce estático:

a) Las fuerzas de roce son reactivas (ver la Sección 1.3.2) porque se oponen a la ocurrencia de un desplazamiento. Como fuerza reactiva, la fricción responde a una demanda. En efecto, en la situación que se presenta en la Fig. 1.8.a no existe fuerza de fricción porque no hay demanda que la haga necesaria, independientemente del grado de rugosidad de los cuerpos en contacto. En la situación que se presenta en la Fig. 1.8.b, al aplicar el hombre una fuerza H se moviliza de inmediato una fuerza de roce R h, de igual dirección pero de sentido contrario, para lograr el equilibrio horizontal del sistema. Es claro que R hdepende de la demanda H, a mayor H mayor R h, porque siempre R h=H para mantener el equilibrio.

b) La fuerza de roce es tangencial a las superficies en contacto, es decir queda contenida en el plano de deslizamiento potencial. Como fuerza reactiva, que se opone al deslizamiento relativo, la fuerza de roce es paralela a la dirección del desplazamiento impedido. La Fig. 1.39 muestra las fuerzas de roce F ren tres situaciones típicas; también se muestran las componentes normales de la reacción (N) que por cierto están presentes. En el caso de apoyo liso F r=0 y sólo existe reacción normal N.

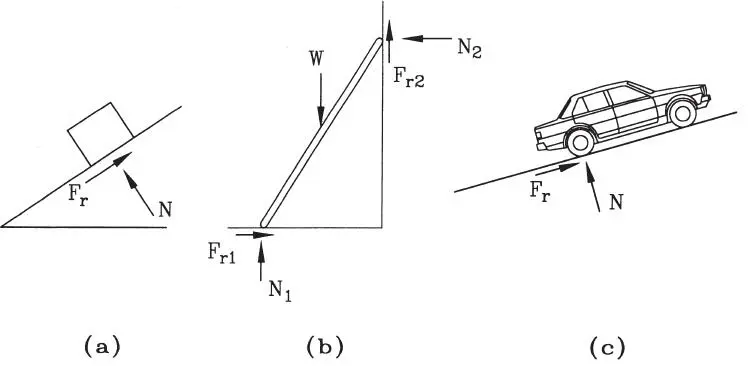
Figura 1.39Dirección tangencial del roce

c) La fuerza de roce que puede desarrollarse entre dos cuerpos tiene un valor límite máximo:

en que μ es el coeficiente de roce estático , que depende de los materiales en contacto y las condiciones de sus superficies, y de N, que es la fuerza normal de contacto perpendicular a la superficie tangencial de deslizamiento potencial. Cuando la fuerza de fricción F rexcede F maxse rompe el equilibrio estático y se inicia el deslizamiento. Generalmente el deslizamiento continúa porque el coeficiente de roce cinemático μ ces aún menor que μ . Cuando la fuerza de fricción es idéntica a F maxse dice que el cuerpo se encuentra en la condición límite de equilibrio o a punto de deslizar. Cuando la fuerza de fricción F res menor que F maxel cuerpo puede encontrarse en equilibrio.

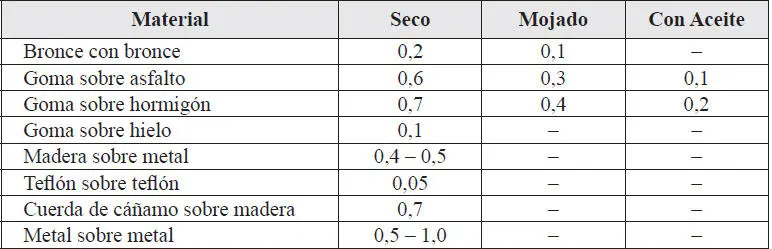
Valores típicos del coeficiente de roce se presentan en la Tabla 1.1. Debe notarse sin embargo que ellos sólo tienen valor referencial, ya que pueden variar ampliamente dependiendo de las distintas calidades de cada material, del acabado de las superficies y su limpieza, de la temperatura, y por cierto en alto grado de la presencia de agua o lubricación.

d) El coeficiente de roce μ, es independiente de la fuerza normal N y no depende del área de contacto de los cuerpos involucrados. El hecho de que el contacto se realice en un área pequeña, manteniendo N constante, sólo involucra una presión de contacto mayor, pero no altera a μ ni a la fuerza de roce máxima F max.

TABLA 1.1Valores Típicos del Coeficiente de Roce Estático

Como se mencionó antes, el valor de μ para cada caso específico es muy incierto. Afortunadamente, sin embargo, su valor puede determinarse mediante un experimento muy simple. Este consiste en disponer una rampa de inclinación variable hecha de uno de los materiales y colocar sobre ella el segundo material, como ilustra la Fig. 1.40.a. Para cualquier inclinación ϕ, las fuerzas que actúan sobre el bloque y el correspondiente polígono de fuerzas se muestran en las Figs. 1.40.b y c.

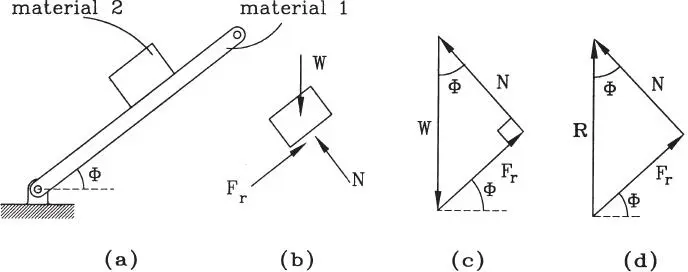
Figura 1.40Determinación del coeficiente de roce

El experimento consiste en aumentar progresivamente el ángulo ϕ hasta alcanzar ϕ maxcompatible con el equilibrio, es decir hasta que se inicie el deslizamiento del bloque. En referencia a la Fig. 1.40.c, con ϕ=ϕ maxy utilizando el Teorema de Lamy, las ecuaciones de equilibrio son:

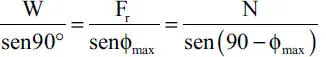
utilizando la segunda igualdad se tiene

pero por ser la situación límite de equilibrio, la fuerza de fricción alcanzó su valor máximo, luego

igualando las Ecs. 1-37 y 1-38 se tiene

con lo cual, medido ϕ maxen el experimento, se obtiene el coeficiente de roce μ entre ambos materiales.

La explicación del experimento anterior se presta para introducir el concepto de ángulo de roce , que corresponde a la inclinación máxima respecto a la normal que puede adoptar la fuerza interna total entre dos superficies en contacto. En la Fig. 1.40.b la reacción se planteó en términos de las componentes normal al plano N y tangencial al plano F r. Por supuesto la reacción total R es la suma de ellas dos, como muestra la Fig. 1.40.d, y por cierto R es vertical, e igual en magnitud y sentido contrario a W, pues el equilibrio exige R=W. Como puede apreciarse en la Fig. 1.40.d, R forma ángulo ϕ con la normal, o sea, forma ángulo ϕ con el plano inclinado. El experimento antes descrito puede entonces interpretarse diciendo que en la medida que se aumenta la inclinación de la rampa, se obliga a cambiar la inclinación de R con respecto al plano inclinado, aunque su magnitud se mantiene siempre constante igual a W y su dirección se mantiene siempre vertical. La pérdida de equilibrio al alcanzar ϕ maxse explica entonces porque las superficies en contacto no son capaces de desarrollar una reacción interna con inclinación mayor a ϕ max. La máxima inclinación, o ángulo de roce, se relaciona con el coeficiente de fricción según la Ec. 1.39, de donde: