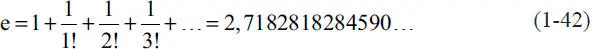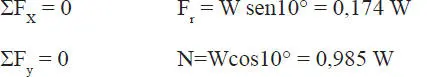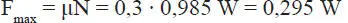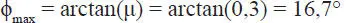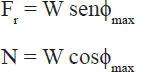Rafael Riddell Carvajal - Fundamentos de ingeniería estructural para estudiantes de arquitectura

La interpretación geométrica del ángulo de roce máximo ϕ maxes el llamado cono de roce . Si se tiene una partícula sobre una superficie cualquiera, para mantenerla en equilibrio en contacto con la superficie, la reacción R de la superficie sobre la partícula debe encontrarse sobre o al interior del cono generado por las infinitas rectas que forman ángulo ϕ maxcon la normal a la superficie en el punto de contacto (Fig. 1.41). Cuando R está justo sobre el cono, la partícula se encuentra en estado límite de equilibrio.

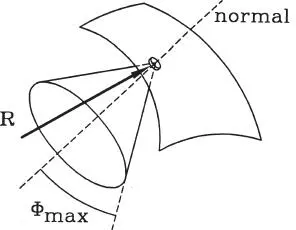
Figura 1.41Cono de roce

Otra aplicación de la fricción se encuentra en el caso de cuerdas o correas en contacto con superficies rugosas. Por ejemplo, la Fig. 1.42.a muestra una cuerda real pesada que descansa en reposo sobre la rama de un árbol, aunque sin duda el peso de las partes colgantes es diferente como muestra la Fig. 1.42.b. Este tipo de fricción se utiliza mucho en máquinas, para transmitir el movimiento de un elemento rotatorio a otro, casos muy conocidos son la correa del ventilador de un automóvil, o la correa de la antigua máquina de coser movilizada con los pies. Una importante aplicación industrial es la correa transportadora, que consiste en una banda sin fin para acarrear granos, minerales, o productos molidos en general; el movimiento de la banda de goma se mantiene por contacto rugoso con un cilindro motriz accionado por un motor.

Por el contrario, hay ocasiones en que se desea minimizar el roce de contacto, utilizándose para ello dispositivos como las poleas. Cuando puede ignorarse el roce, por ser despreciable, se usan modelos de contacto liso, como muestran las Figs. 1.42.c y d; la propiedad fundamental en este caso es que la tensión T de la cuerda se mantiene constante, independiente de la longitud de contacto con el apoyo liso y de los ángulos de despegue de la cuerda a ambos lados de la curva de apoyo.

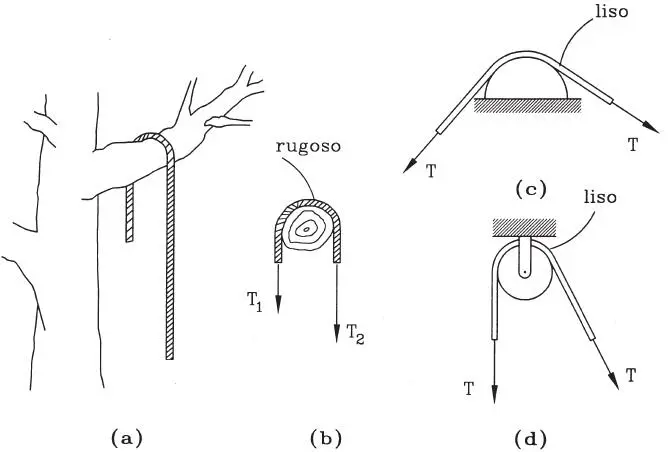
Figura 1.42Cuerdas en contacto rugoso (a y b) y lisos (c y d)

Para analizar el estado de equilibrio límite de una cuerda liviana en contacto con una superficie cualquiera rugosa, considérese la Fig. 1.43. La cuerda está en contacto con la curva entre los puntos A y B donde se despega de ella, siendo tangente a la curva en dichos puntos. En A y B se han trazado las normales a la curva (perpendiculares a la tangente), las que se intersectan en 0 formando el ángulo β. Suponiendo que la cuerda está a punto de deslizar hacia la izquierda, a lo largo del camino entre A y B se desarrollan fuerzas de fricción en el contacto, designadas por f, que se oponen al deslizamiento (sentido contrario a T), y fuerzas normales n. Estas fuerzas, que podrían considerarse actuando en pequeños segmentos de la cuerda, no son constantes sino dependen de la curvatura de la superficie en el punto de contacto; en efecto, a mayor curvatura mayores son n y f (f=μn), mientras que si no hay curvatura (contacto plano) n y f son nulas. Por simplicidad, en la Fig. 1.43 se muestran con las mismas letras a todo el largo del contacto, pero en rigor son distintas en cada punto. Claramente T > T oya que, para romper el equilibrio, la fuerza T debe vencer a T omás todas las fuerzas de fricción a lo largo del contacto. La evaluación de la relación entre T y T orequiere usar cálculo integral (ver Riley y Sturges, 1995), lo que se omitirá aquí, llegándose a la expresión:

En que e es un número notable en matemáticas que corresponde a la base de los logaritmos naturales (la función logaritmo natural, designada por ln , es tal que si para dos números reales dados se cumple que ln (a)=b implica que e b=a). El número e corresponde al resultado de la serie infinita

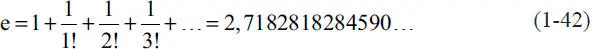
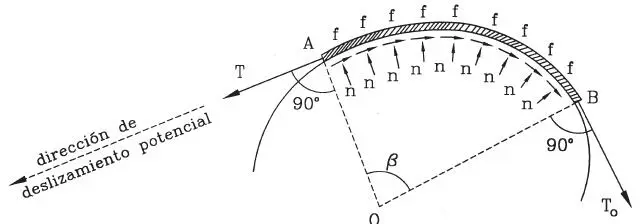
Figura 1.43Cuerda sobre superficie rugosa

Por su parte β, como muestra la Fig. 1.43, es el ángulo de contacto, o ángulo entre las normales en los puntos de tangencia, el que debe expresarse en radianes. Los radianes son una unidad de medida de ángulos: una circunferencia completa, es decir un ángulo de 360°, equivale a 2π radianes. La conversión de β de grados a radianes se obtiene entonces de la proporción

Ejemplo 1.13

Un bloque de peso W se encuentra sobre un plano inclinado en 10° como muestra la Fig. E1.13.a. El coeficiente de fricción entre ambos materiales es μ=0,3. a) ¿Está el bloque en equilibrio?; b) ¿Para qué inclinación del plano se rompería el equilibrio?, c) En la condición límite de equilibrio, ¿cuál es la magnitud de las componentes normal y tangencial de la reacción? y ¿cuál es la reacción total?.

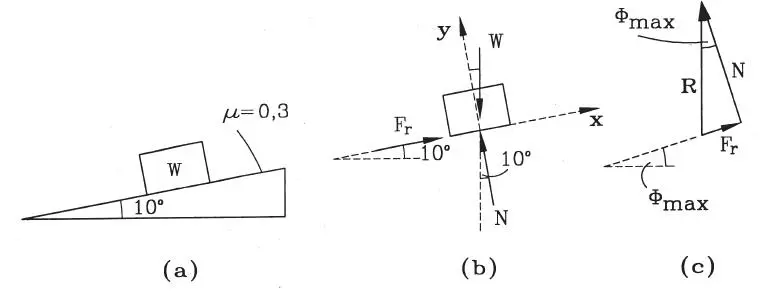
Figura E1.13

Solución:

a) La única forma de que el bloque pierda el equilibrio es que no haya suficiente fricción para sostenerlo. Entonces, para responder la pregunta hay que analizar las reacciones del plano sobre el bloque. Para ello considérese la Figura E1.13.b, que muestra el diagrama de cuerpo libre del bloque con las fuerzas externas que actúan sobre él. Se muestra también un sistema de ejes de referencia respecto de los cuales las ecuaciones de equilibrio son:

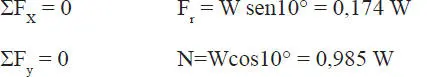
La máxima fuerza de roce que podría desarrollarse es

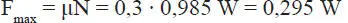
como F rmaxel bloque está en equilibrio.

b) La máxima inclinación posible corresponde al ángulo de roce (Ec. 1-40):

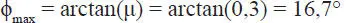
También podrían haberse usado las ecuaciones de la parte (a) con la incógnita ϕ maxen vez de 10º:

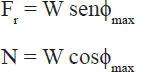
pero por tratarse de la condición límite de equilibrio F r= μN, luego