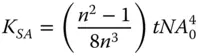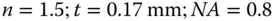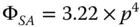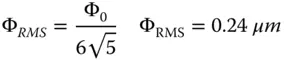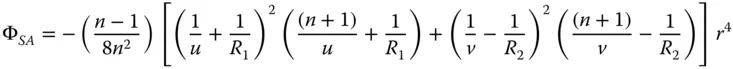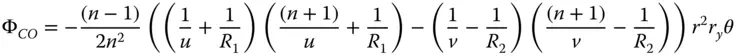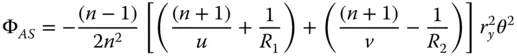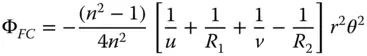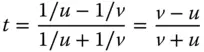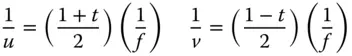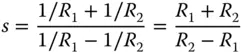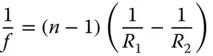Worked Example 4.2 Microscope Cover Slip
A microscope cover slip 0.17 mm thick is to be used with a microscope objective with a numerical aperture of 0.8. The refractive index of the cover slip is 1.5. What is the root mean square (rms) spherical aberration produced by the cover slip? The aberration is illustrated in Figure 4.7.
From Eq. (4.24):
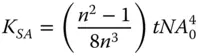
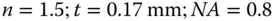
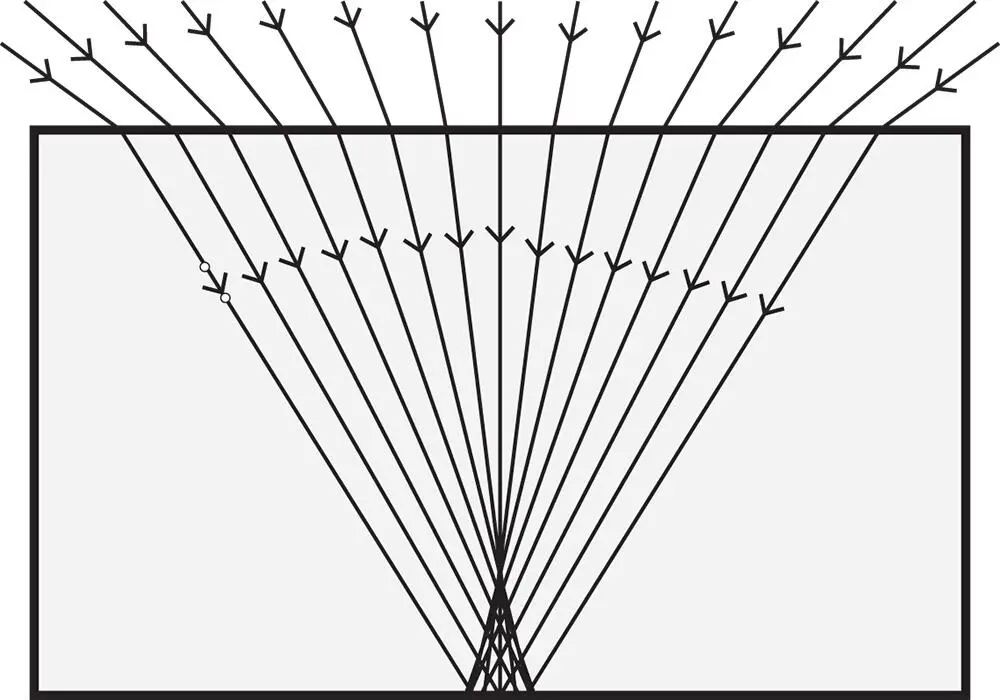
Figure 4.7 Spherical aberration in cover slip.
Substituting the above values we get: K sa= 0.003 22 mm or 3.2 μm.
The wavefront error (in microns) is thus given by:
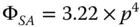
where p is the normalised pupil function.
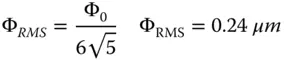
For reasons that will become apparent later, in practice, wavefront errors are usually expressed as a fraction of some standard wavelength, for example 589 nm. The above wavefront error represents about 0.4 × λ when expressed in this way. An rms wavefront error of about λ/14 is considered consistent with good image quality. This level of aberration is, therefore, significant and measures must be taken (within the objective) to correct for it.
4.4.2 Aberrations of a Thin Lens
We extend the treatment already outlined to analyse a thin lens. A thin lens can be considered as combination of two refractive surfaces, where the distance between the two surfaces is ignored. In practice, this is a reasonable assumption, provided the thickness is much less than the radii of the surfaces in question. Of course, the wavefront error produced by the two surfaces is simply the sum of the aberrations of the individual surfaces. A schematic for the analysis is shown in Figure 4.8.
The wavefront error contribution for the first surface is very easy to compute; it is simply that set out in Eqs. (4.5a)– (4.5d). To compute the contribution for the second surface, one can analyse this using the same methodology as in Section 4.2, but exploiting natural symmetry. That is to say, one can analyse the second surface by rotating the whole surface about the y axis, such that z → −z and x → −x. In this event, for the second surface, R → − R 2, u → v , θ → −θ. It is then simply a case of substituting these values into the formulae in Eqs. (4.5a)– (4.5d)and adding the wavefront error contribution of the first surface. The total wavefront error for the thin lens is then:
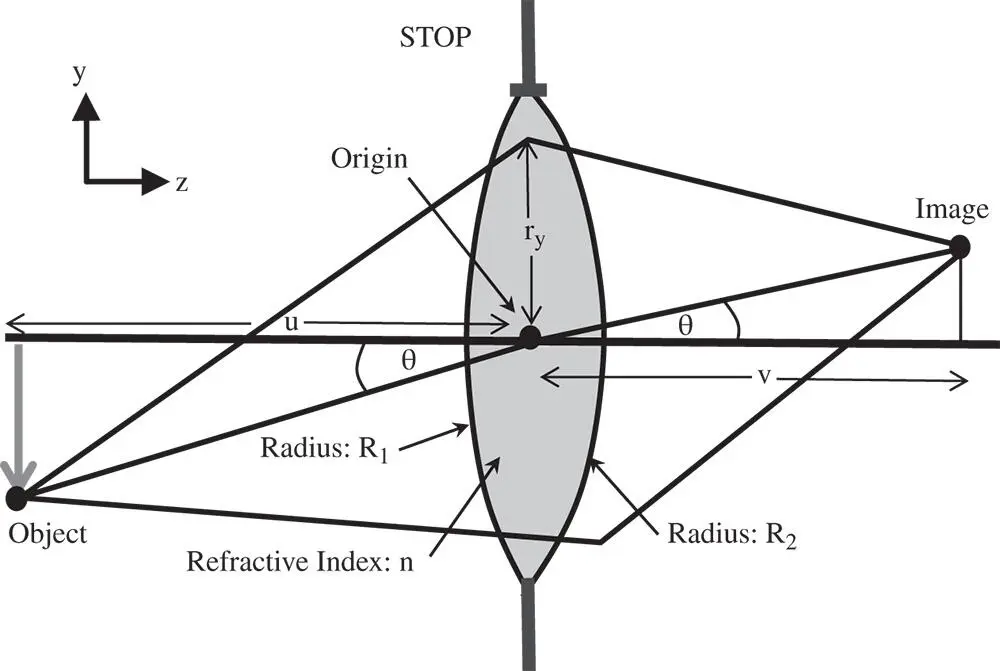
Figure 4.8 Aberration analysis for thin lens.
(4.25a) 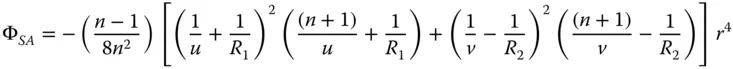
(4.25b) 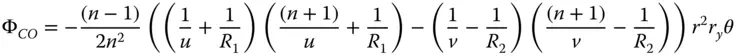
(4.25c) 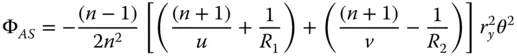
(4.25d) 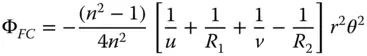
4.4.2.1 Conjugate Parameter and Lens Shape Parameter
In terms of gaining some insight into the behaviour of a thin lens, the formulae in Eqs. (4.25a)– (4.25d)are a little opaque. It would be somehow useful to express the aberrations of a thin lens directly in terms of its focusing power and some other parameters. The first of these other parameters is the so called conjugate parameter, t . The conjugate parameter is defined as below:
(4.26) 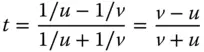
As we are dealing with a thin lens, we can use the thin lens formula to calculate the focal length, f , of the lens:

This, in turn, leads to expressions for u and v :
(4.27) 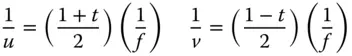
Figure 4.9illustrates the conjugate parameter schematically. The infinite conjugate is represented by a conjugate parameter of ±1. If the conjugate parameter is +1, then the image is at infinity. Conversely, a conjugate parameter of −1 is associated with an object located at the infinite conjugate. In the symmetric scenario where object and image distances are identical, then the conjugate parameter is zero. As illustrated in Figure 4.9, where the conjugate parameter is greater than 1, then the object is real and the image is virtual. Finally, where the conjugate parameter is less than −1, then the object is virtual and the image is real.
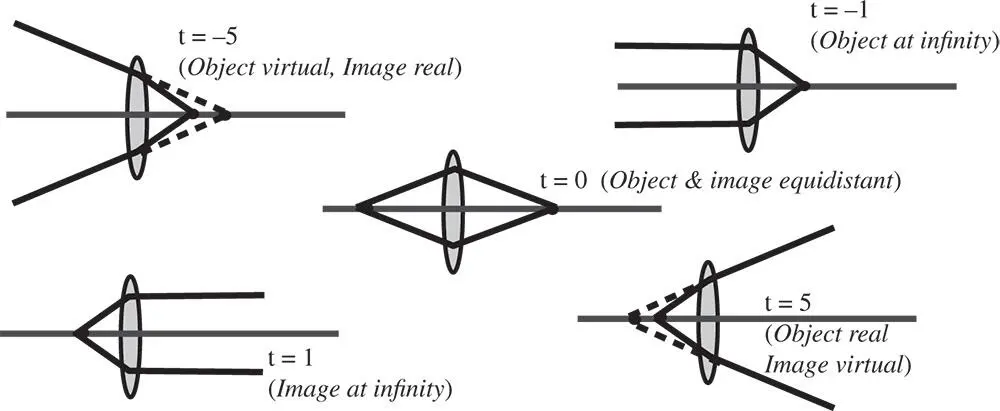
Figure 4.9 Conjugate parameter.
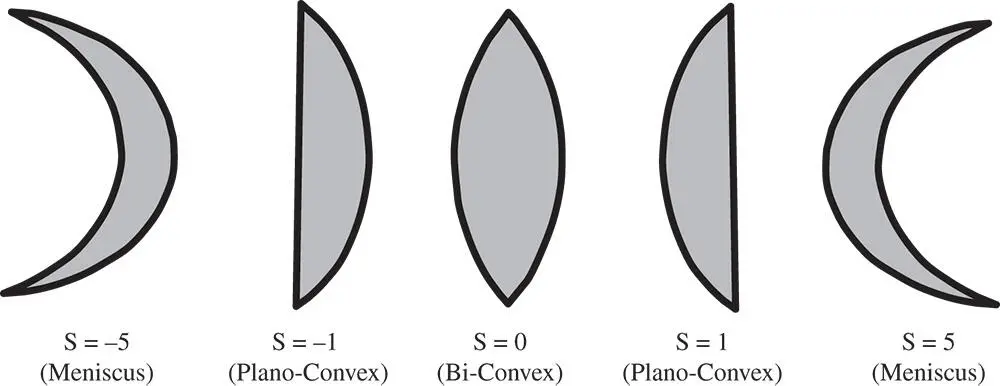
Figure 4.10 Coddington lens shape parameter.
We have thus described object and image location in terms of a single parameter. By analogy, it is also useful to describe a lens in terms of its focal power and a single parameter that describes the shape of the lens. The lens, of course, is assumed to be defined by two spherical surfaces, with radii R 1and R 2, defining the first and second surfaces respectively. The shape of a lens is defined by the so-called Coddington lens shape factor, s, which is defined as follows:
(4.28) 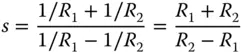
As before, the power of the lens may be expressed in terms of the lens radii:
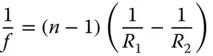
where n is the lens refractive index .
As with the conjugate parameter and the object and image distances, the two lens radii can be expressed in terms of the lens power and the shape factor, s .
Читать дальше