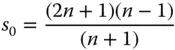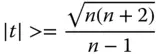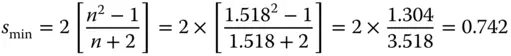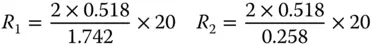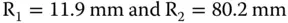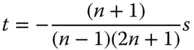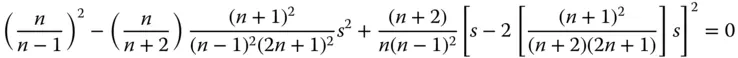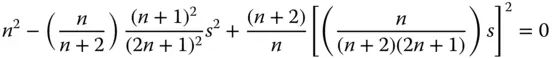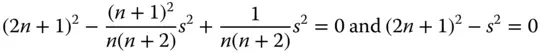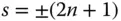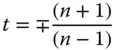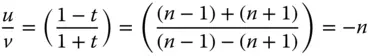Stephen Rolt - Optical Engineering Science

(4.37)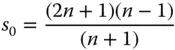

For a refractive index of 1.5, this minimum condition is met for a shape factor of 0.8. This is similar, but not quite the same as the optimum for spherical aberration. Again, the most curved surface should face the infinite conjugate. Overall behaviour is illustrated in Figure 4.12.

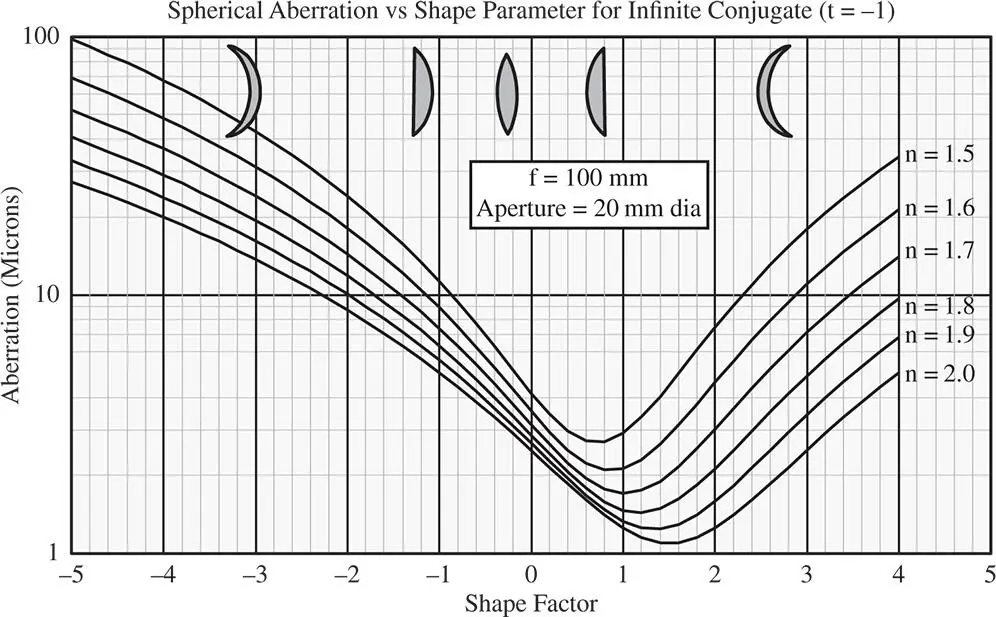
Figure 4.11 Spherical aberration vs. shape parameter for a thin lens.

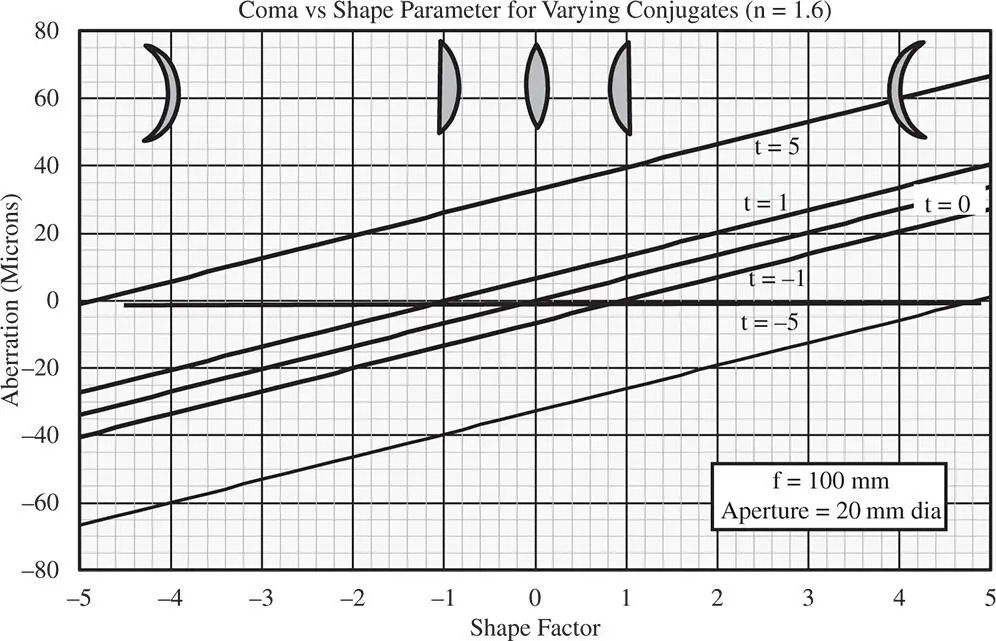
Figure 4.12 Coma vs lens shape for various conjugate parameters.

Once again, this specifically applies to the situation where the stop is at the lens surface. Of course, as stated previously, neither astigmatism nor field curvature are affected by shape or conjugate parameter.

Although it is impossible to reduce spherical aberration for a thin lens to zero at the infinite conjugate, it is possible for other conjugate values. In fact, the magnitude of the conjugate parameter must be greater than a certain specific value for this condition to be fulfilled. This magnitude is always greater than one for reasonable values of the refractive index and so either object or image must be virtual. It is easy to see from Eq. (4.31a)that this threshold value should be:

(4.38)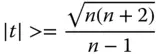

For n = 1.5, this threshold value is 4.58. That is to say for there to be a shape factor where the spherical aberration is reduced to zero, the conjugate parameter must either be less than −4.58 or greater than 4.58. Another point to note is that since spherical aberration exhibits a quadratic dependence on shape factor, where this condition is met, there are two values of the shape factor at which the spherical aberration is zero. This behaviour is set out in Figure 4.13which shows spherical aberration as a function of shape factor for a number of difference conjugate parameters.

A thin lens is to be used to focus a Helium-Neon laser beam. The focal length of the lens is to be 20 mm and the lens is required to be ‘best form’ to minimise spherical aberration. The refractive index of the lens is 1.518 at the laser wavelength of 633 nm. Calculate the required shape factor and the radii of both lens surfaces. From Eq. (4.35)we have:

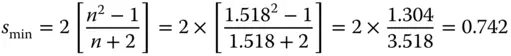
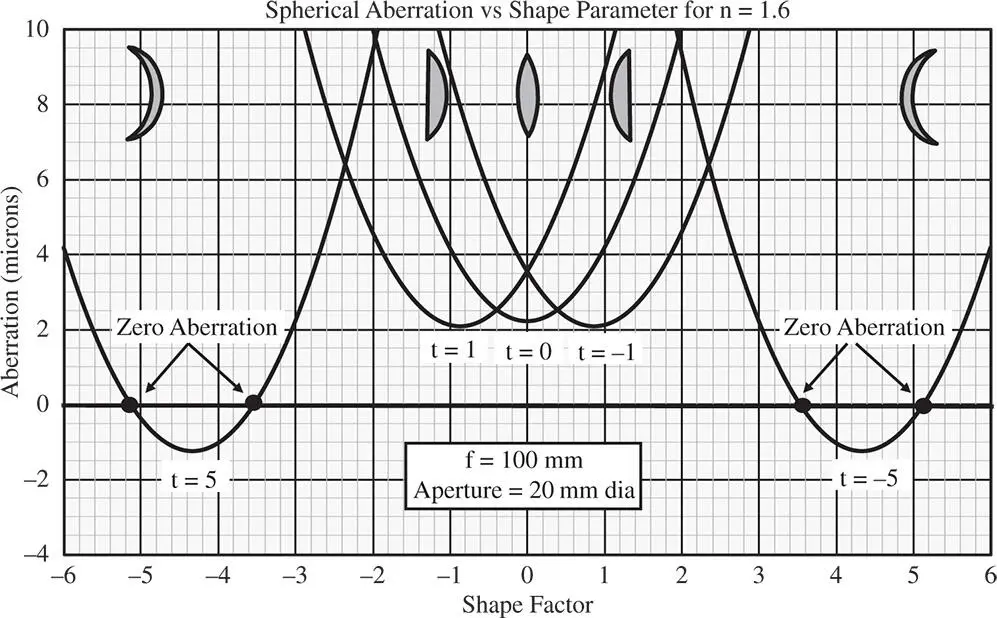
Figure 4.13 Spherical aberration vs shape factor for various conjugate parameter values.

The optimum shape factor is 0.742 and we can use this to calculate both radii given knowledge of the required focal length. Rearranging Eq. (4.29)we have:

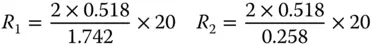
This gives:

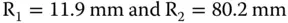
It is the surface with the greatest curvature, i.e. R1, that should face the infinite conjugate (the parallel laser beam).

Just as in the case of a single surface, it is possible to find a conjugate and lens shape pair that produce neither spherical aberration nor coma. For reasons outlined previously, it is not possible to eliminate astigmatism or field curvature for a lens of finite power. If the spherical aberration is to be zero, it must be clear that for the aplanatic condition to apply, then either the object or the image must be virtual. Equations (4.31a)and (4.31b)provide two conditions that uniquely determine the two parameters, s and t . Firstly, the requirement for coma to be zero clearly relates s and t in the following way:

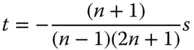
Setting the spherical aberration to zero and substituting for t we have the following expression given entirely in terms of s :

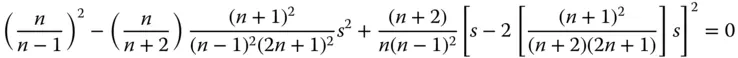
and

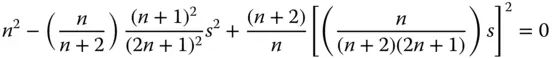
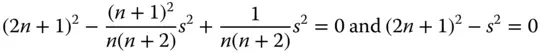
Finally this gives the solution for s as:

(4.39a)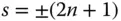

Accordingly the solution for t is

(4.39b)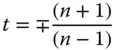

Of course, since the equation for spherical aberration gives quadratic terms in s and t , it is not surprising that two solutions exist. Furthermore, it is important to recognise that the sign of t is the opposite to that of s . Referring to Figure 4.10, it is clear that the form of the lens is that of a meniscus. The two solutions for s correspond to a meniscus lens that has been inverted. Of course, the same applies to the conjugate parameter, so, in effect, the two solutions are identical, except the whole system has been inverted, swapping the object for image and vice-versa.

An aplanatic meniscus lens is an important building block in an optical design, in that it confers additional focusing power without incurring further spherical aberration or coma. This principle is illustrated in Figure 4.14which shows a meniscus lens with positive focal power.

It is instructive, at this point to quantify the increase in system focal power provided by an aplanatic meniscus lens. Effectively, as illustrated in Figure 4.14, it increases the system numerical aperture in (minus) the ratio of the object and image distance. For the positive meniscus lens in Figure 4.14, the conjugate parameter is negative and equal to −( n + 1)/( n − 1). From Eq. (4.27)the ratio of the object and image distances is given by:

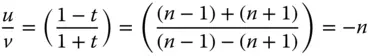
As previously set out, the increase in numerical aperture of an aplanatic meniscus lens is equal to minus the ratio of the object and image distances. Therefore, the aplanatic meniscus lens increases the system power by a factor equal to the refractive index of the lens. This principle is of practical consequence in many system designs. Of course, if we reverse the sense of Figure 4.14and substitute the image for the object and vice versa, then the numerical aperture is effectively reducedby a factor of n.