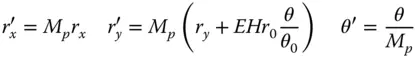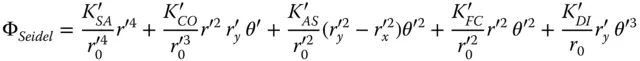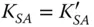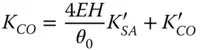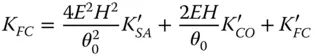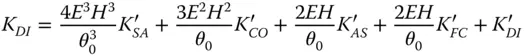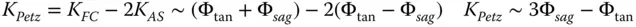Stephen Rolt - Optical Engineering Science

(4.42)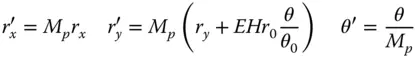

The angle, θ 0is representative of the maximum system field angle and helps to define the eccentricity parameter and the Lagrange invariant. We already know the OPD when cast in terms of r x ′ , r y ′ , and θ, as this is as per the analysis for the case where the stop is at the optic itself. That is to say, the expression for the OPD is as given in Eqs. and these aberrations defined in terms of K SA ′ , K CO ′ , K AS ′ , K FC ′ , and K DI ′ . Therefore, the total OPD attributable to the five Gauss-Seidel aberrations is given by:

(4.43)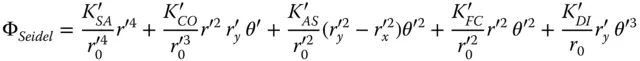

To determine the aberrations as expressed by the pupil co-ordinates for the new stop location, it is a simple matter of substituting Eq. (4.42)into Eq. (4.43). This results in the so-called stop shift equations:

(4.44a)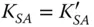

(4.44b)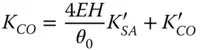

(4.44c)

(4.44d)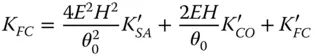

(4.44e)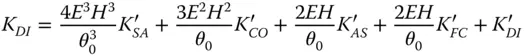

What this set of equations reveals is that there exists a ‘hierarchy’ of aberrations. Spherical aberration may be transmuted into coma, astigmatism, field curvature, and distortion by shifting the stop position. Similarly, coma may be transformed into astigmatism, field curvature, and distortion and both astigmatism and field curvature may produce distortion. However, coma can never produce spherical aberration and neither astigmatism nor field curvature is capable of generating spherical aberration or coma. Equation (4.44e)reveals, for the first time, that it is possible to generate distortion by shifting the stop. Our previous idealised analysis clearly suggested that distortion is not produced where the lens or optical surface is located at the stop.

Another important conclusion relating to Eqs. (4.44a)– (4.44e)is the impact of stop shift on the astigmatism and field curvature. Inspection of Eqs. (4.44c)and (4.44d)reveals that the change in field curvature produced by stop shift is precisely double that of the change in astigmatism in all cases. Therefore, the Petzval curvature, which is given by K FC−2 K ASremains unchanged by stop shift. This further serves to demonstrate the fact that the Petzval curvature is a fundamental system attribute and is unaffected by changes in stop location and, indeed component location. Petzval curvature only depends upon the system power. Thus, it is important to recognise that the quantity K FC−2 K ASis preserved in any manipulation of existing components within a system. If we express the Petzval curvature in terms of the tangential and sagittal curvature we find:

(4.45)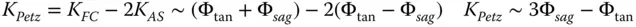

Since K Petzis not changed by any manipulation of component or stop positions, Eq. (4.45)implies that any change in the sagittal curvatureis accompanied by a change three times as large in the tangential curvature. This is an important conclusion.

For small shifts in the position of the stop, the eccentricity parameter is proportional to that shift. Based on this and examining Eqs. (4.44a)– (4.44e), one can come to some general conclusions. For a system with pre-existing spherical aberration, additional coma will be produced in linear proportion to the stop shift. Similarly, the same spherical aberration will produce astigmatism and field curvature proportional to the square of the stop shift. The amount of distortion produced by pre-existing spherical aberration is proportional to the cube of the displacement. Naturally, for pre-existing coma, the additional astigmatism and field curvature produced is in proportion to the shift in the stop position. Additional distortion is produced according to the square of the stop shift. Finally, with pre-existing astigmatism and field curvature, only additional distortion may be produced in direct proportion to the stop shift.

As an example, a simple scenario is illustrated in Figure 4.16. This shows a symmetric system with a biconvex lens used to image an object in the 2 f – 2 f configuration. That is to say, the conjugate parameter is zero. In this situation, the coma may be expected, by virtue of symmetry, to be zero. For a simple lens, the distortion is also zero. The spherical aberration is, of course, non-zero, as are both the astigmatism and field curvature.

Using basic modelling software, it is possible to analyse the impact of small stop shifts on system aberration. The results are shown in Figure 4.17.

Clearly, according to Figure 4.17, the spherical aberration remains unchanged as predicted by Eq. (4.44a). For small shifts, the amount of coma produced is in proportion to the shift. Since there is no coma initially, the only aberration that can influence the astigmatism and field curvature is the pre-existing spherical aberration. As indicated in Eqs. (4.44c)and (4.44d), there should be a quadratic dependence of the astigmatism and field curvature on stop position. This is indeed borne out by the analysis in Figure 4.17. Similarly, the distortion shows a linear trend with stop position, mainly influenced by the initial astigmatism and field curvature that is present.

Although, in practice, these stop shift equations may not find direct use currently in optimising real designs, the underlying principles embodied are, nonetheless, important. Manipulation of the stop position is a key part in the optimisation of complex optical systems and, in particular, multi-element camera lenses. In these complex systems, the pupil is often situated between groups of lenses. In this case, the designer needs to be aware also of the potential for vignetting, should individual lens elements be incorrectly sized.

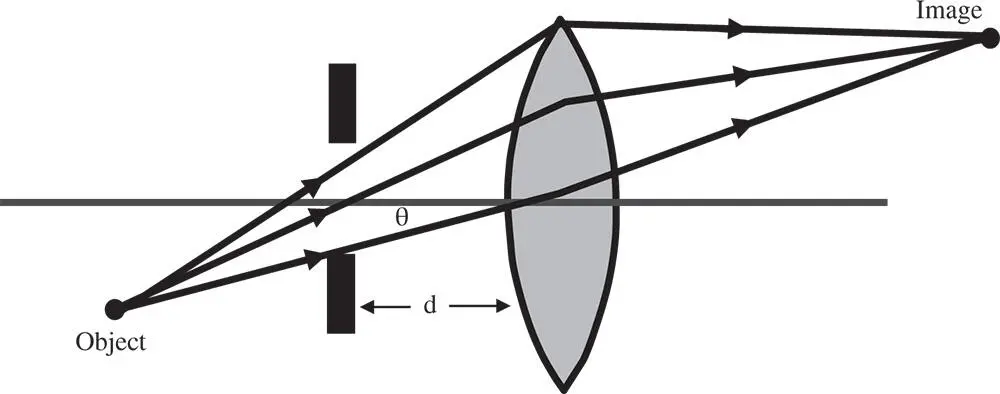
Figure 4.16 Simple symmetric lens system with stop shift.

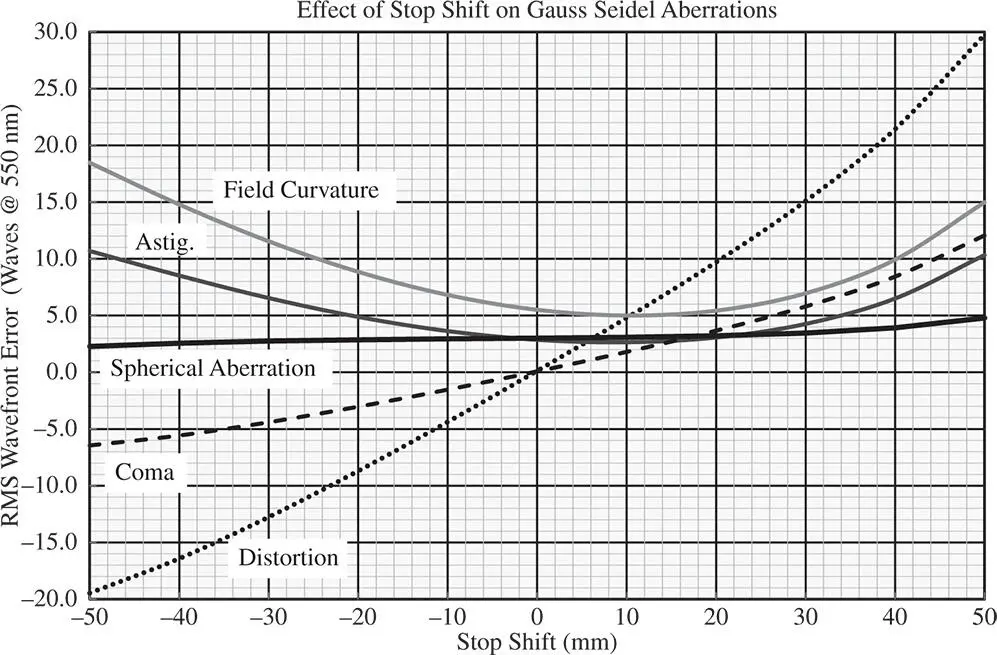
Figure 4.17 Impact of stop shift for simple symmetric lens system.

The stop shift equations provide a general insight into the impact of stop position on aberration. Most significant is the hierarchy of aberrations. For example, no fundamental manipulation of spherical aberration may be accomplished by the manipulation of stop position. Otherwise, there some special circumstances it would be useful for the reader to be aware of. For example, in the case of a spherical mirror, with the object or image lying at the infinite conjugate, the placement of the stop at the mirror's centre of curvature altogether removes its contribution to coma and astigmatism; the reader may care to verify this.