Stephen Rolt - Optical Engineering Science

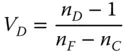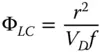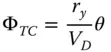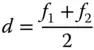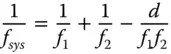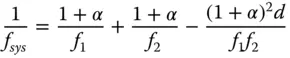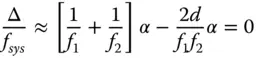
Figure 4.20 Refractive index variation with wavelength for SCHOTT BK7 glass material.

Because of the historical importance of the visible spectrum, glass materials are typically characterised by their refractive properties across this portion of the spectrum. More specifically, glasses are catalogued in terms of their refractive indices at three wavelengths, nominally ‘blue’, ‘yellow’, and ‘red’. In practice, there are a number of different conventions for choosing these reference wavelengths, but the most commonly applied uses two hydrogen spectral lines – the ‘Balmer-beta’ line at 486.1 nm and the ‘Balmer-alpha’ line at 656.3, plus the sodium ‘D’ line at 589.3 nm. The refractive indices at these three standard wavelengths are symbolised as n F, n C, and n Drespectively. At this point, we introduce the Abbe number, V D, which expresses a glass's dispersion by the ratio of its optical power to its dispersion:

(4.48)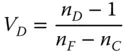

The numerator in Eq. (4.48)represents the effective optical or focusing power at the ‘yellow’ wavelength, whereas the denominator describes the dispersion of the glass as the difference between the ‘blue’ and the ‘red’ indices. It is important to recognise that the higher the Abbe number, then the less dispersive the glass, and vice versa. Abbe numbers vary, typically between about 20 and 80. Broadly speaking, these numbers express the ratio of the glass's focusing power to its dispersion. Hence, for a material with an Abbe number of 20, the focal length of a lens made from this material will differ by approximately 5% (1/20) between 486.1 and 656.3 nm.

The most obvious effect of chromatic aberration is that light is broad to a different focus for different wavelengths. This effect is known as longitudinal chromatic aberrationand is illustrated in Figure 4.21.

As can be seen from Figure 4.21, light at the shorter, ‘blue’ wavelengths are focused closer to the lens, leading to an axial (longitudinal) shift in the paraxial focus for the different wavelengths. In summary, longitudinal chromatic aberration is associated with a shift in the paraxial focal position as a function of wavelength. Thus the effect of longitudinal chromatic aberration is to produce a blur spot or transverse aberration whose magnitude is directly proportional to the aperture size, but is independent of field angle. However, there are situations where, to all intents and purposes, all wavelengths share the same paraxial focal position, but the principal points are not co-located. That is to say, whilst all wavelengths are focused at a common point, the effective focal length corresponding to each wavelength is not identical. This scenario is illustrated in Figure 4.22.

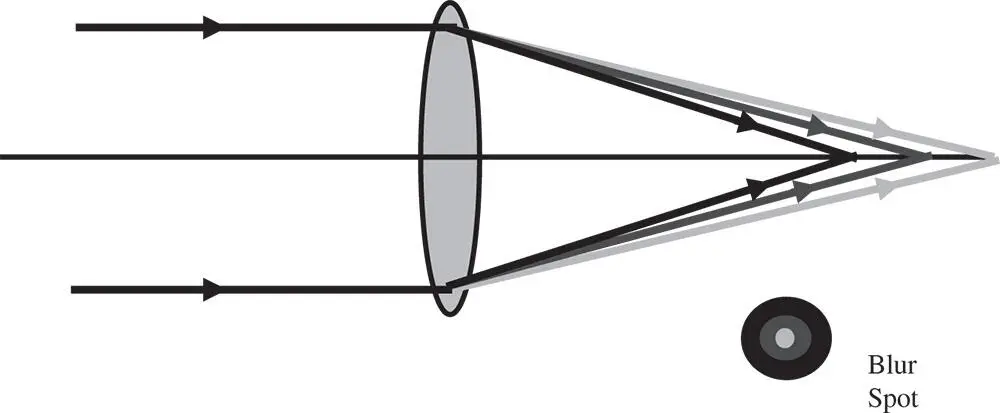
Figure 4.21 Longitudinal chromatic aberration.

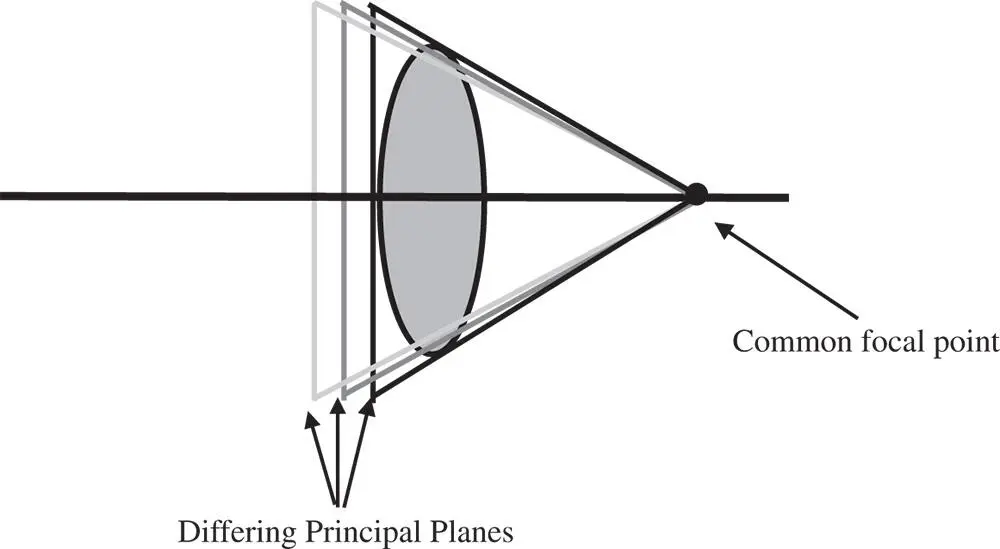
Figure 4.22 Transverse chromatic aberration.

The effect illustrated is known as transverse chromatic aberrationor lateral colour. Whilst no distinct blurring is produced by this effect, the fact that different wavelengths have different focal lengths inevitably means that system magnification varies with wavelength. As a result, the final image size or height of a common object depends upon the wavelength. This produces distinct coloured fringing around an object and the size of the effect is proportional to the field angle, but independent of aperture size.

Hitherto, we have cast the effects of chromatic aberration in terms of transverse aberration. However, to understand the effect on the same basis as the Gauss-Seidel aberrations, it is useful to express chromatic aberration in terms of the OPD. When applied to a single lens, longitudinal chromatic aberration simply produces defocus that is equal to the focal length divided by the Abbe number. Therefore, the longitudinal chromatic aberration is given by:

(4.49a)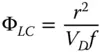

f is the focal length of the lens and r the pupil position .

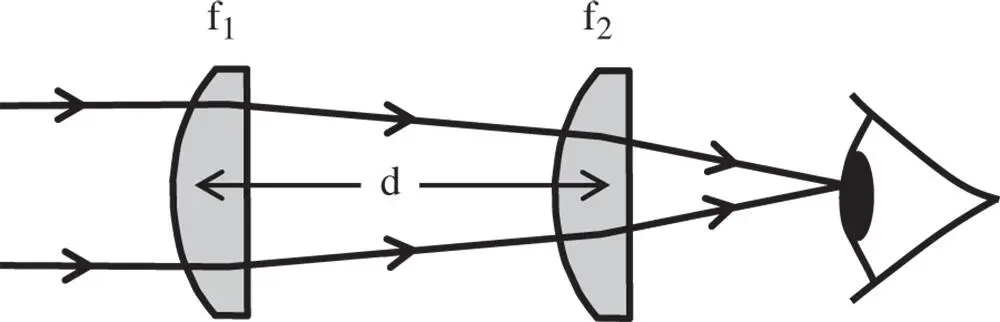
Figure 4.23 Huygens eyepiece.

Similarly, the transverse chromatic aberration can be expressed as an OPD:

(4.49b)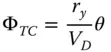

Examining Eqs. (4.49a)and (4.49b)reveals that the ratio of transverse to longitudinal aberration is given by the ratio of the field angle to the numerical aperture. In practice, for optical elements, such as microscope and telescope objectives, the field angle is very much smaller than the numerical aperture and thus longitudinal chromatic aberration may be expected to predominate. For eyepieces, the opposite is often the case, so the imperative here is to correct lateral chromatic aberration.

A practical example of the correction of lateral chromatic aberration is in the Huygens eyepiece. This very simple, early, eyepiece uses two plano-convex lenses separated by a distance equivalent to half the sum of their focal lengths. This is illustrated in Figure 4.23.

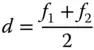
Since we are determining the impact of lateral chromatic aberration, we are only interested in the effective focal length of the system comprising the two lenses. Using simple matrix analysis as described in Chapter 1, the system focal length is given by:

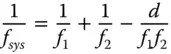
If we assume that both lenses are made of the same material, then their focal power will change as a function of wavelength by a common proportion, α. In that case, the system focal power at the new wavelength would be given by:

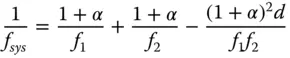
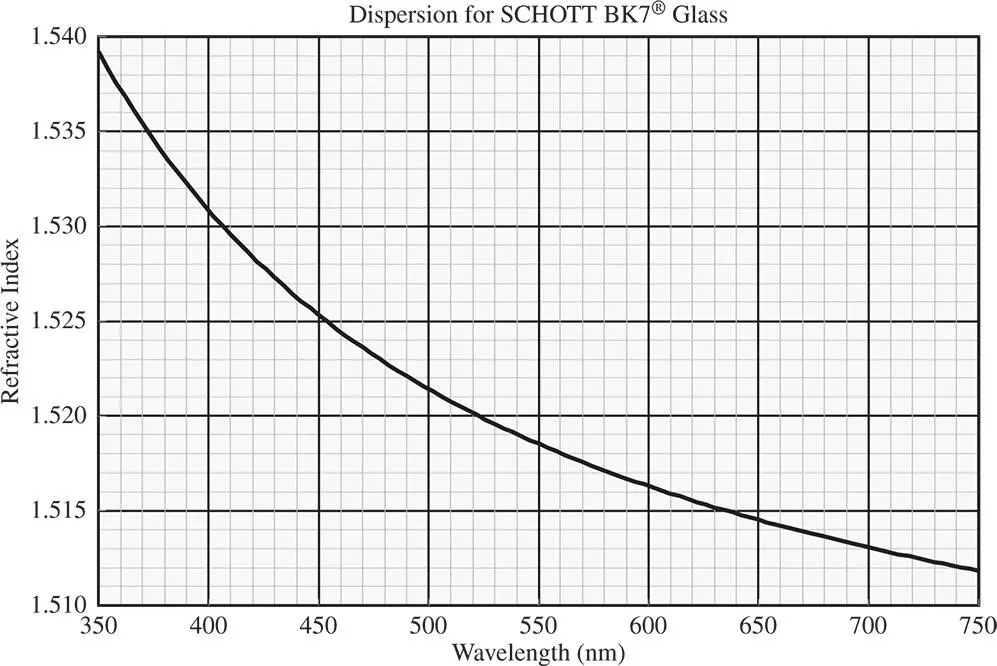
For small values of α, we can ignore terms of second order in α, so the change in system power may be approximated by:

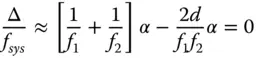
The change in system power should be zero and this condition unambiguously sets the lens separation, d, for no lateral chromatic aberration: