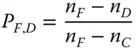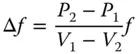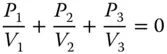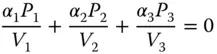Stephen Rolt - Optical Engineering Science

Figure 4.26clearly shows the effect as a quadratic dependence in focal shift with wavelength, with the ‘red’ and ‘blue’ wavelengths in focus, but the central wavelength with significant defocus. In line with the notion that we are seeking to quantify a quadratic effect, we can define the partial dispersion coefficient, P , as:

(4.57)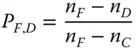

If we measure the impact of secondary colour as the difference in focal length, Δ f , between the ‘blue’ and ‘red’ and the ‘yellow’ focal lengths for an achromatic doublet corrected in the conventional way we get:

(4.58)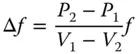

where f is the lens focal length.

The secondary colour is thus proportional to the difference between the two partial dispersions. For simplicity, we have chosen to represent the partial dispersion in terms of the same set of wavelengths as used in the Abbe number. However, whilst the same central (n d) wavelength might be used, some wavelength other than the n F, hydrogen line might be chosen for the partial dispersion. Nevertheless, this does not alter the logic presented in Eq. (4.58). Correcting secondary colour is thus less straightforward when compared to the correction of primary colour. Unfortunately, in practice, there is a tendency for the partial dispersion to follow a linear relationship with the Abbe number, as illustrated in the partial dispersion diagram shown in Figure 4.27, illustrating the performance of a range of glasses.

Thus, in the case of the achromatic doublet, judicious choice of glass pairs can minimise secondary colour, but without eliminating it. In principle, secondary colour can be entirely corrected in a triplet system employing lenses of different materials. More formally, if we describe the three lenses as having focal powers of P 1, P 2, and P 3, with the Abbe numbers represented as V 1, V 2, and V 3and the partial dispersions as, α 1, α 2, α 3, then the lens powers may be uniquely determined from the following set of equations:

(4.59a)

(4.59b)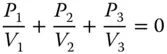

(4.59c)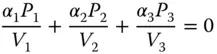

As indicated previously, Figure 4.27exemplifies the close link between primary and secondary dispersion, with a linear trend observed linking the partial dispersion and the Abbe number for most glasses. It is easy to demonstrate by presenting Eqs. (4.59a)– (4.59c)in matrix form that, if a wholly linear relationship exists between partial dispersion and Abbe number, then the matrix determinant will be zero. In this instance, a triplet solution is therefore impossible. Furthermore, the same analysis suggests that for a set of glasses lying close to a straight line on the partial dispersion plot will necessitate the deployment of lenses with very high countervailing powers. It is clear, therefore, that an optimum triplet design is afforded by selection of glasses that depart as far as possible from a straight-line plot on the partial dispersion diagram. In this context, the isolated group of glasses that appear in Figure 4.27, the fluorite glasses, are especially useful in correcting for secondary colour. These glasses lie particularly far from the general trend line for the ‘main series’ of glasses. Lenses which are corrected for both primary and secondary colour are referred to as apochromaticlenses. These lenses invariably incorporate fluorite glasses.

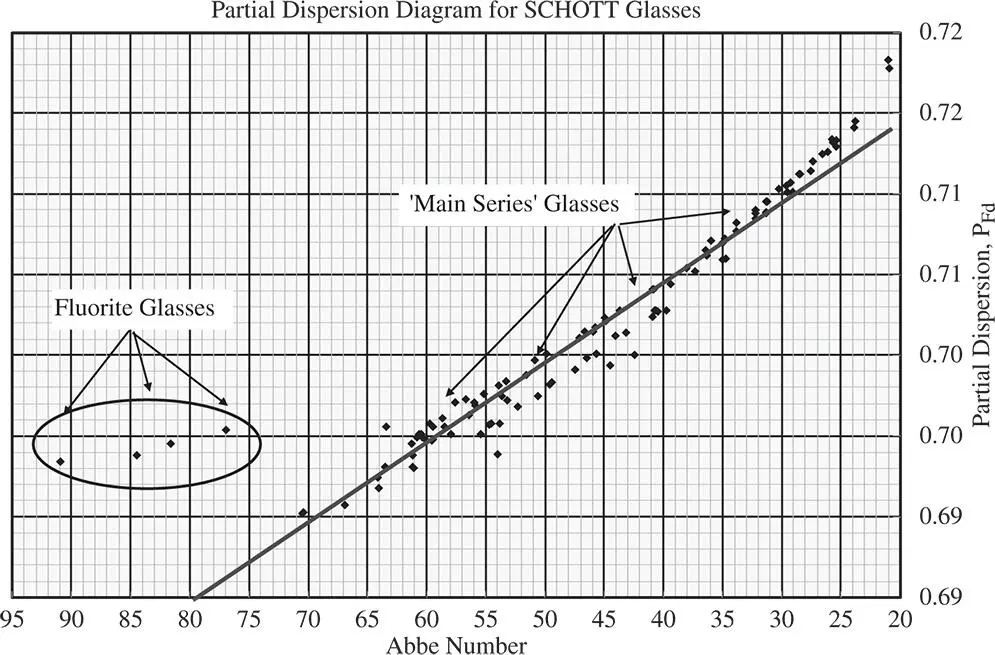
Figure 4.27 Plot of partial dispersion against Abbe number.

In the previous analysis we learned that the basic design of simple doublet lenses allowed for the correction of both chromatic aberration and spherical aberration. Furthermore, this flexibility for correction could be extended to coma for an air spaced lens. However, since the refractive index of the two glasses in a doublet lens varies with wavelength, then inevitably, so does the spherical aberration. As such, spherical aberration can only be corrected at one wavelength, e.g. at the ‘D’ wavelength. This means that there will be some uncorrected spherical aberration at the extremes of the spectrum. This effect is known as spherochromatism. It is generally less significant in magnitude when compared with secondary colour.

For some specific applications, such as telescope and microscope objective lenses, the field angles tend to be very much smaller than the angles associated with the system numerical aperture. In these instances, the off-axis aberrations, such as coma, are much less significant than the on-axis aberrations. Therefore, as far as the Gauss-Seidel aberrations are concerned, there exists a hierarchy of aberrations that can be placed in order of their significance or importance:

1 Spherical Aberration

2 Coma

3 Astigmatism and Field Curvature

4 Distortion

That is to say, it is of the greatest importance to correct spherical aberration and then coma, followed by astigmatism, field curvature, and distortion. This emphasises the significance and use of aplanatic elements in optical design.

Of course, for certain optical systems, this logic is not applicable. For instance, in both camera lenses and in eyepieces, the field angles are very substantial and comparable to the angles associated with the numerical aperture. Indeed, in systems of this type, greater emphasis is placed upon the correction of astigmatism, field curvature, and distortion than in other systems.

With these comments in mind, it would be useful to summarise all the aberrations covered in this chapter and to classify them by virtue of their pupil and field angle dependence. Table 4.1sets out the wavefront error dependence upon pupil and field angle for each of the aberrations.

It would be instructive, at this point, to take the example of the 200 mm doublet and to plot the wavefront aberrations attributable to some of the aberrations listed in Table 4.1against numerical aperture. Spherochromatism is expressed as the difference in spherical aberration wavefront error between the n Fand n Cwavelengths (486.1 and 656.3 nm). Secondary colour is expressed as the wavefront error attributable to the difference in defocus between the n Fand n Dwavelengths (486.1 and 589.3 nm). A plot is shown in Figure 4.28.

It is clear that for the simple achromat under consideration, at least for modest lens apertures, the impact of secondary colour predominates. If a wavefront error of about 50 nm is consistent with ‘high quality’ imaging, then secondary colour has a significant impact for numerical apertures in excess of 0.05 or f#10. With numerical apertures in excess of 0.2 (f#2.5), higher order spherical aberration starts to make a significant contribution. On the other hand the effect of spherochromatism is more modest throughout. In this context, the impact of spherochromatism would only be a significant issue if secondary colour were first corrected.