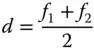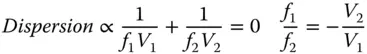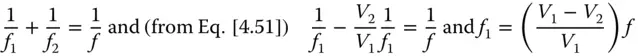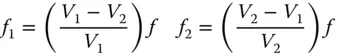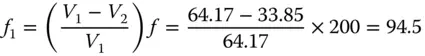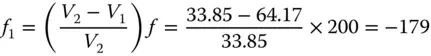Stephen Rolt - Optical Engineering Science

(4.50)

If this condition is fulfilled, then the Huygens eyepiece will have no transverse chromatic aberration. However, it must be emphasised that this condition does not provide immunity from longitudinal chromatic aberration.

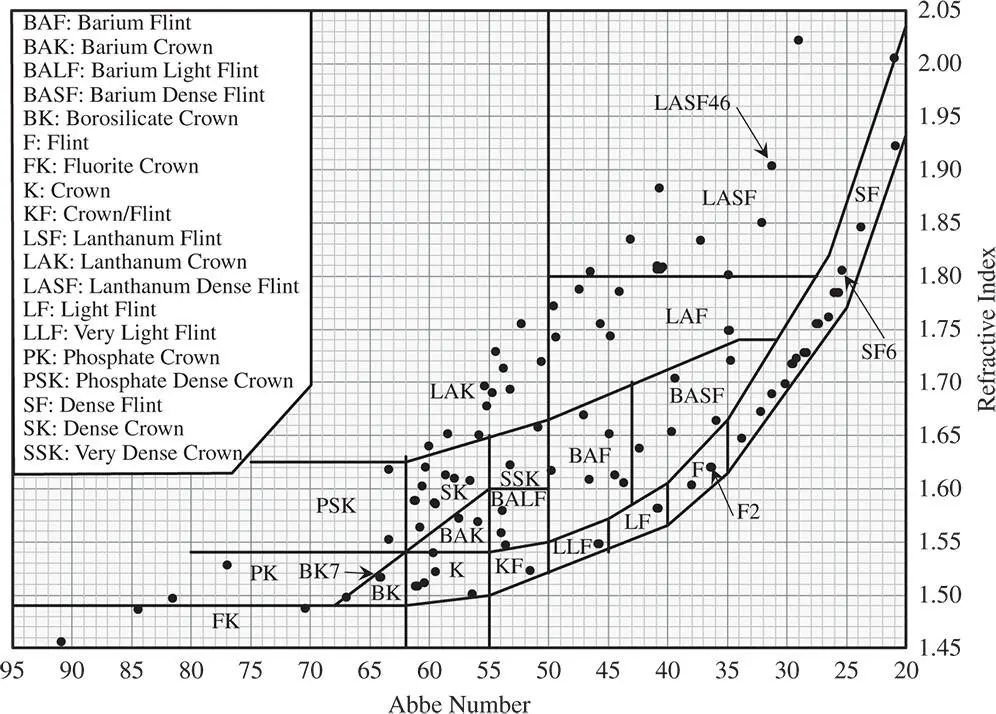
Figure 4.24 Abbe diagram.

For visible applications, the Abbe number for a glass is of equal practical importance as the refractive index itself. The Abbe diagram is a simple graphic tool that captures the basic refractive properties of a wide range of optical glasses. It comprises a simple 2D map with the horizontal axis corresponding to the Abbe number and the vertical axis to the glass index. A representative diagram is shown in Figure 4.24.

By referring to this diagram, the optical designer can make appropriate choices for specific applications in the visible. In particular, it helps select combinationsof glasses leading to a substantially achromatic design. One special and key application is the achromatic doublet. This lens is composed of two elements, one positive and one negative. The positive lens is a high power (short focal length) element with low dispersion and the negative lens is a low power element with high dispersion. Materials are chosen in such a way that the net dispersion of the two elements cancel, but the powers do not. This will be considered in more detail in the next section.

The different zones highlighted in the Abbe diagram replicated in Figure 4.24refer to the elemental composition of the glass. For example, ‘Ba’ refers to the presence of barium and ‘La’ to the presence of lanthanum. Originally, many of the dense, high index glasses used to contain lead, but these are being phased out due to environmental concerns. The Abbe diagram reveals a distinct geometrical profile with a tendency for high dispersion to correlate strongly with refractive index. In fact, it is the presence of absorption features within the glass (at very much shorter wavelengths) that give rise to the phenomenon of refraction and these features also contribute to dispersion.

As introduced previously, the achromatic doublet is an extremely important building block in a transmissive (non-mirror) optical design. The function of an achromatic doublet is illustrated in Figure 4.25.

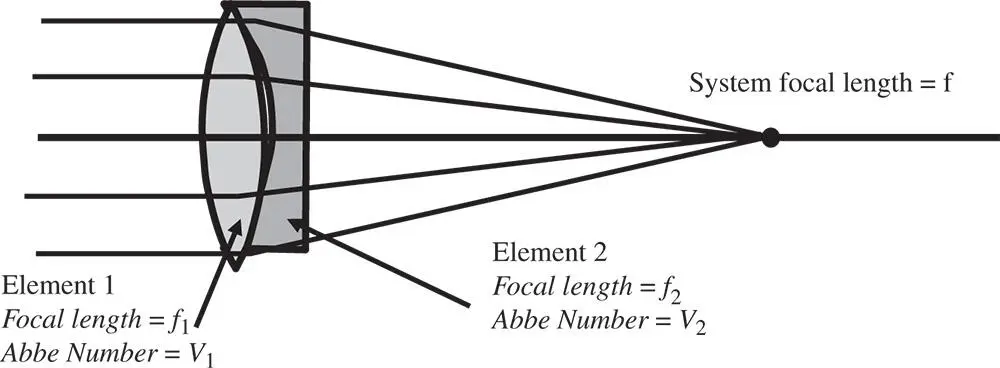
Figure 4.25 The achromatic doublet.

The first element, often (on account of its shape) referred to as the ‘crown element’, is a high power positive lens with low dispersion. The second element is a low power negative lens with high dispersion. The focal lengths of the two elements are f 1and f 2respectively and their Abbe numbers V 1and V 2. Since the intention is that the dispersions of the two elements should entirely cancel, this condition constrains the relative power of the two elements. Individually, the dispersion as measured by the difference in optical power between the red and blue wavelengths is proportional to the reciprocal of the focal power and the Abbe number for each element. Therefore:

(4.51)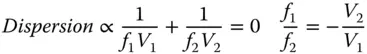

From Eq. (4.51), it is clear that the ratio of the two focal lengths should be minus the inverse of the ratio of their respective Abbe numbers. In other words, the ratio of their powers should be minus the ratio of their Abbe numbers. The power of the system comprising the two lenses is, in the thin lens approximation, simply equal to the sum of their individual powers. Therefore, it is possible to calculate these individual focal lengths, f 1and f 2, in terms of the desired system focal length of f:

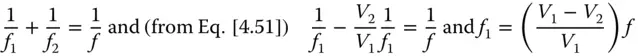
Thus, the two focal lengths are simply given by:

(4.52)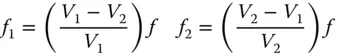

In the thin lens approximation, therefore, light will be focused at the same point for the red and blue wavelengths. Consequentially, in this approximation, this system will be free from both longitudinal and transverse chromatic aberration. The simplicity of this approach may be illustrated in a straightforward worked example.

We wish to construct and achromatic doublet with a focal length of 200 mm. The two glasses to be used are: SCHOTT N-BK7 for the positive crown lens and SCHOTT SF2 for the negative lens. Both these glasses feature on the Abbe diagram in Figure 4.24and the Abbe number for these glasses are 64.17 and 33.85 respectively. The individual focal lengths may be calculated using Eq. (4.52):

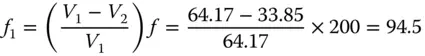
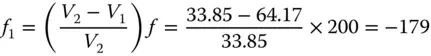
Therefore, the focal length of the first ‘crown lens’ should be 94.5 mm and the focal length of the second diverging lens should be −179 mm.

Thus far, the analysis design of an achromatic doublet has been fairly elementary. In the previous worked example, we have constrained the focal lengths of the two lens elements to specific values. However, we are still free to choose the shape of each lens. That is to say, there are two further independent variables that can be adjusted. Achromatic doublets can either be cemented or air spaced. In the case of the cemented doublet, as presented in Figure 4.25, the second surface of the first lens must have the same radius as the first surface of the second lens. This provides an additional constraint; thus, for the cemented doublet, there is only one additional free variable to adjust. However, introduction of an air space between the two lenses removes this constraint and gives the designer an extra degree of freedom to play with. That said, the cemented doublet does offer greater robustness and reliability with respect to changes in alignment and finds very wide application as a standard optical component.

As a ‘stock component’ achromatic doublets are designed, generally, for the infinite conjugate. For cemented doublets, with the single additional degree of design freedom, these components are optimised to have zero spherical aberration at the central wavelength. This is an extremely important consideration, for not only are these doublets free of chromatic aberration, but they are also well optimised for other aberrations. Commercial doublets are thus extremely powerful optical components.