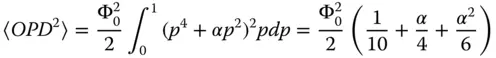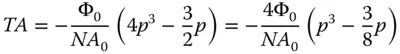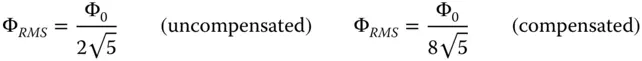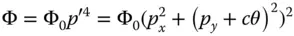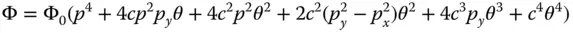In this instance, the plot has a characteristic ‘W’ shape, with the curve in the vicinity of the origin dominated by the quadratic defocus term. As with the case for transverse aberration, the defocus can be optimised to produce the minimum possible OPD value when taken as a root mean squared value over the circular pupil. Again, using a weighting factor that is proportional to the pupil function, p , (to take account of the circular geometry), the mean squared OPD is given by:
(3.15) 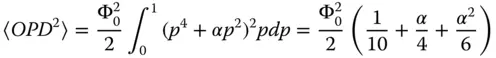
Figure 3.8 Quartic OPD fan.

Figure 3.9 OPD fan with balancing defocus.
The above expression has a minimum where α = −¾. To understand the magnitude of this defocus, it is useful first to convert the new OPD expression into a transverse aberration using Eq. (3.12).
(3.16) 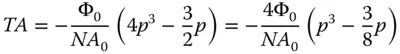
From Eq. (3.16), it can be seen that the optimum defocus is 3/8 of the distance between the paraxial and marginal ray foci. This value is different to that derived for the optimisation of the transverse aberration itself. It should be understood that the optimisation of the transverse aberration and the OPD, although having the same ultimate purpose in minimising the aberration, nonetheless produce different results. Indeed, in the optimisation of optical designs, one is faced with a choice of minimising either the geometrical spot size (transverse aberration) or OPD in the form of rms WFE. The rationale behind this selection will be considered in later chapters when we examine measures of image quality, as applied to optical design.
The balanced defocus, as illustrated in Eq. (3.15)does significantly reduce the rms OPD. In fact, it reduces the OPD by a factor of four. Resultant rms values are set out in Eq. (3.17).
(3.17) 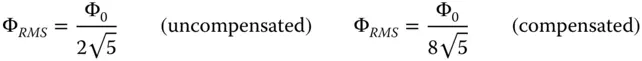
3.4 General Third Order Aberration Theory
Armed with a simple understanding of the basic concepts that lie behind the description of third order aberration, we can proceed to a more general and more powerful analysis. This analysis relies on a theoretical treatment of OPD as a measure of aberration. As pointed out earlier, although the lowest order aberration (beyond the paraxial approximation) has a fourth order dependence upon pupil function, this theory is still referred to as third order aberration theory. In the example we have hitherto considered, we have analysed an on axis object located at the infinite conjugate. For the more general treatment, we must consider off-axis objects with the chief ray having some non-zero field angle with respect to the optical axis. In addition, the object may have an arbitrary axial location and we must also consider the axial position of the pupil.
This third order theory is referred to as Gauss-Seidel aberration theoryand is of general applicability to optical systems of arbitrary complexity. There is, however, one important constraint. The theory assumes that the entire geometry, component surfaces and so on, is circularly symmetric about the optical axis. In formulating the theory, we assume that the object presents a non-zero field angle, θ, with respect to the optic axis which is assumed to be oriented along the z axis. The chief ray is tilted by rotation about the x axis, so the object is offset from the optical axis in the y direction. The third order aberrations are to be expressed in terms of the field angle, θ, and the normalised pupil function, p . However, in this instance, because of the non-zero field angle, the rotational symmetry of the pupil is removed, so that separate x and y components of the pupil function, p x, p y, must be introduced.
The assumption in the Gauss-Seidel theory is that the underlying third order aberrations in a symmetrical optical system are themselves symmetrical and proportional to the fourth power of the pupil function. However, the finite field angle will effectively introduce an offset in the effective y component of the pupil function, Δ p y, at some arbitrary optical component. This is illustrated in Figure 3.10which shows generically how such an offset may be visualised.
What is suggested by Figure 3.10is that if a co-ordinate transformation is applied in y that is proportional to the field angle, θ, then the ray fan can be made symmetrical about this new optical axis. That is to say, in Figure 3.10b, any aberration generated would, in terms of OPD, simply be proportional to p 4, with respect to the new axis. In arguing that the required offset is proportional to θ, rather than some other trigonometrical function, we are making an approximation based on linearization in θ. This is justified for third order analysis, since any error produced would only be visible in higher order aberration terms (than third order). In Figure (3.10), the pupil is shown at the optical surface under consideration. However, this is not a necessary condition; wherever the pupil is located a symmetrical ray fan may be produced by simple offset of the co-ordinate system in the Y axis.
Thus, by the argument presented here, any third order aberration may be represented by a pupil dependence of p 4augmented by a shift in the y component of the pupil function, Δ p ythat is proportional to the field angle, θ. This is set out in Eq. (3.18), which describes the WFE, Φ, in terms of θ, p , and p y. From this point, we use WFE, rather than OPD as the key descriptor, as we are describing OPDs across the entire pupil. The offset pupil is now denoted by p′
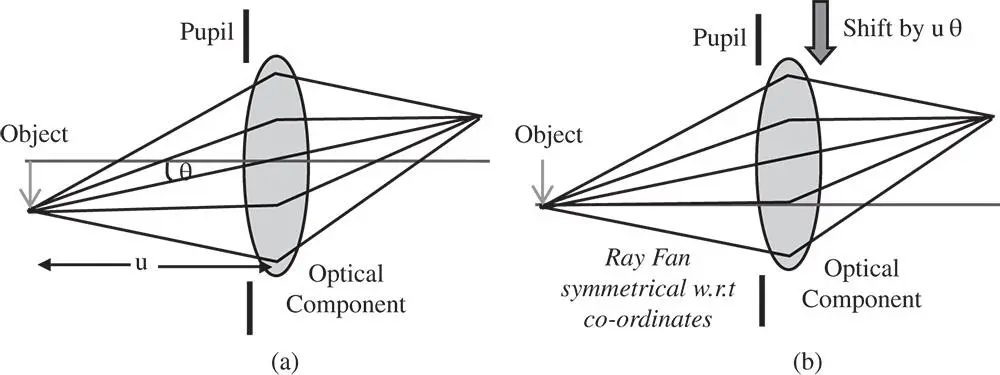
Figure 3.10 (a) Generic layout. (b) Layout with y co-ordinate transformation.
(3.18) 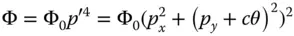
c is a constant of proportionality for the pupil offset .
Equation 3.18may be expanded as follows:
(3.19) 
Finally expanding Eq. (3.19)gives an expression for all third order aberrations:
(3.20) 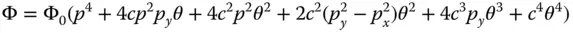
Equation (3.20)contains six distinct terms describing the WFE across the pupil. However, the final term, c 4θ 4, for a given field position, simply describes a constant offset in the optical path or phase of the rays originating from a particular point. That is to say, for a specific ray bundle, no OPD or violation of Fermat's principle could be ascribed to this term, when the difference with respect to the chief ray is calculated. Therefore, the final term in Eq. (3.20)cannot describe an optical aberration. We are thus left with five distinct terms describing third order aberration, each with a different dependence with respect to pupil function and field angle. These are the so called five third order Gauss-Seidel aberrations. Of course, in terms of the WFE dependence, all terms show a fourth order dependence with respect to a combination of pupil function and field angle. That is to say, the sum of the exponents in p and in θ must always sum to 4.
Читать дальше