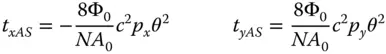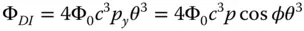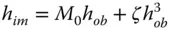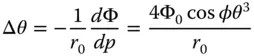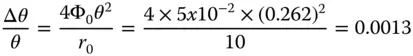Stephen Rolt - Optical Engineering Science

For a general ray, it is possible to calculate the two components of the transverse aberration as a function of the pupil co-ordinates.

(3.33)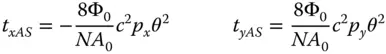

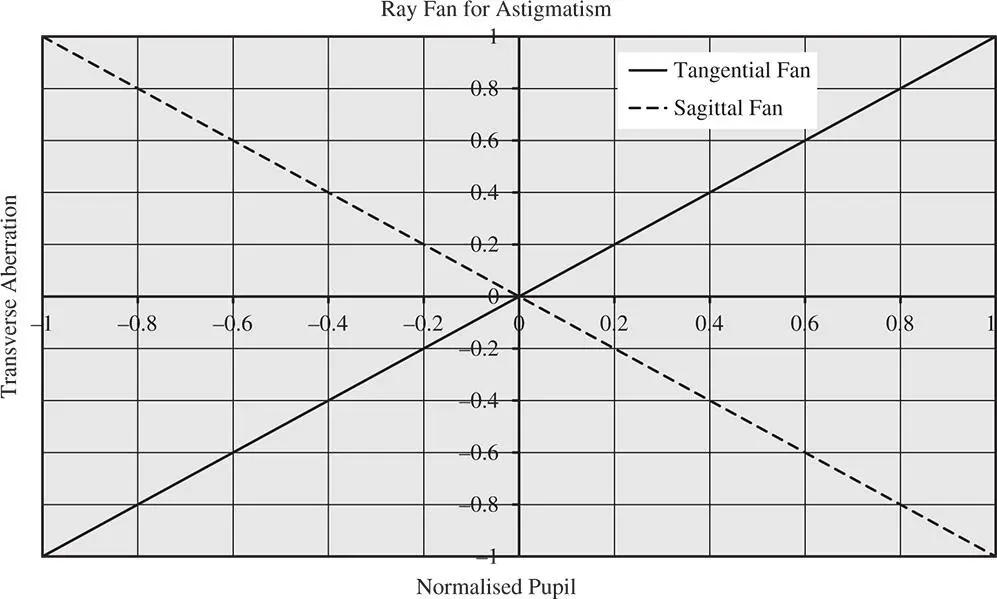
Figure 3.17 Ray fan for astigmatism showing tangential and sagittal fans.

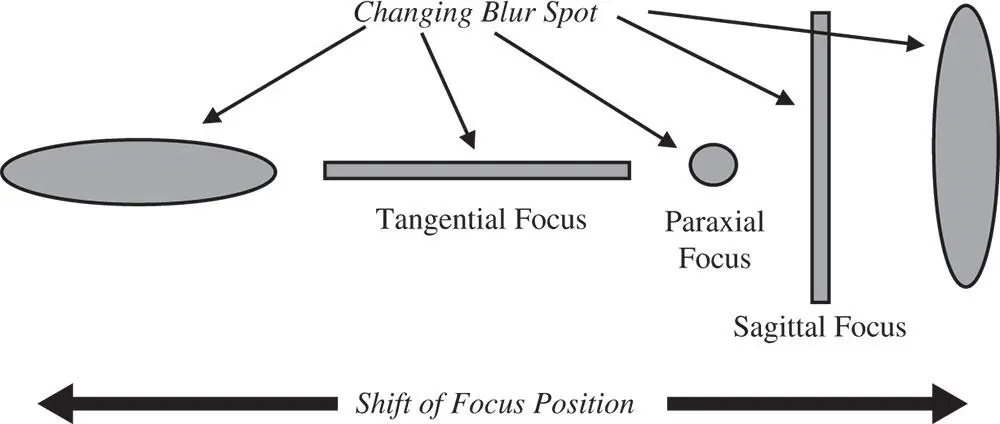
Figure 3.18 Geometric spot vs. defocus for astigmatism.

According to Eq. (3.33), the blur spot produced by astigmatism (at the paraxial focus) is simply a uniform circular disc. Each point in the uniform pupil function simply maps onto a similar point on the blur spot, but with its x value reversed. However, when a uniform defocus is added, similar linear terms (in p) will be added to both t xand t y, having both the same magnitude and sign. As a consequence, the relative magnitude of t xand t ywill change producing a uniform elliptical pattern. Indeed, as mentioned earlier, there are distinct and separate tangential and sagittal foci. At these points, the blur spot is effectively transformed into a line, with the focus along one axis being perfect and the other axis in defocus. This is shown in Figure 3.18.

Due to the even (second order) dependence of OPD upon pupil function, there is no centroid shift evident for astigmatism. For Gauss-Seidel astigmatism, its magnitude is proportional to the square of the field angle. Thus, for an on-axis ray bundle (zero field angle) there can be no astigmatism. This Gauss-Seidel analysis, however, assumes all optical surfaces are circularly symmetric with respect to the optical axis. In the important case of the human eye, the validity of this assumption is broken by the fact that the shape of the human eye, and in particular the cornea, is not circularly symmetrical. The slight cylindrical asymmetry present in all real human eyes produces a small amount of astigmatism, even at zero field angle. That is to say, even for on-axis ray bundles, the tangential and sagittal foci are different for the human eye. For this reason, spectacle lenses for vision correction are generally required to compensate for astigmatism as well as defocus (i.e. short-sightedness or long-sightedness).

The fifth and final Gauss-Seidel aberration term is distortion. The WFE associated with this aberration is third order in field angle, but linear in pupil function. In fact, a linear variation of WFE with pupil function implies a flat, but tilted wavefront surface. Therefore, distortion merely produces a tilted wavefront but without any apparent blurring of the spot. The WFE variation is set out in Eq. (3.34).

(3.34)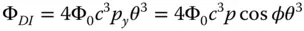

Thus, the only effect produced by distortion is a shift (in the y direction) in the geometric spot centroid; this shift is proportional to the cube of the field angle. However, this shift is global across the entire pupil, so the image remains entirely sharp. The shift is radial in direction, in the sense that the centroid shift is in the same plane (tangential) as the field offset. So, the OPD fan for the tangential fan is linear in pupil function and zero for the sagittal fan. The ray fan is zero for both tangential and sagittal fans, emphasising the lack of blurring.

Taken together with the linear (paraxial) magnification produced by a perfect Gaussian imaging system, distortion introduces another cubic term. That is to say, the relationship between the transverse image and object locations is no longer a linear one; magnification varies with field angle. If the height of the object is h oband that of the image is h im, then the two quantities are related as follows:

(3.35)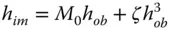

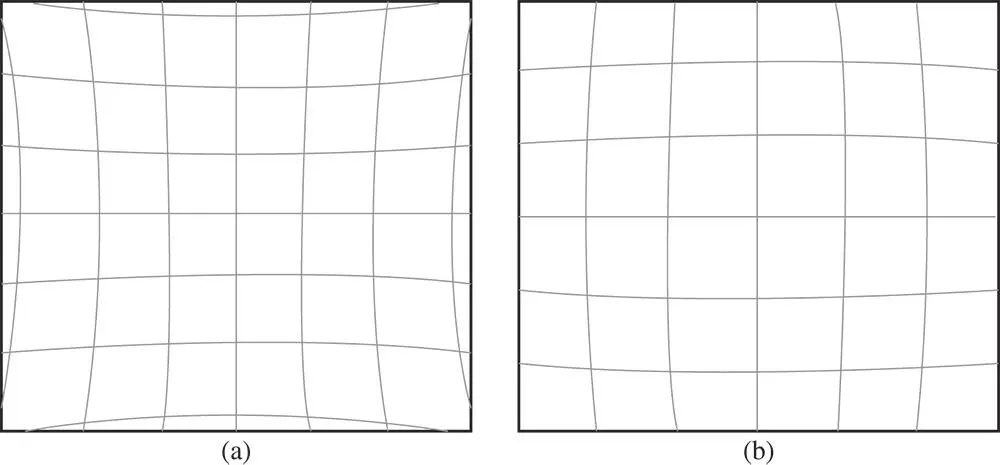
Figure 3.19 (a) Pincushion (positive) distortion. (b) Barrel (negative) distortion.

M 0 is the paraxial magnification; ζ is a constant quantifying distortion

If we denote the x and y components of the object and image location by x ob, y oband x im, y imrespectively, then we obtain:

(3.36)

From Eq. (3.35), it is clear that an object represented by straight line that is offset from the optical axis in object space will be presented as a parabolic line in image space. As such, the image is clearly distorted. The sense and character of the distortion is governed by the sign and magnitude of ζ. This is shown in Figures 3.19a,b.

Where ζ and the distortion is positive, the distortion is referred to as pincushion distortion, as suggested by the form shown in Figure 3.19a. On the other hand, if ζ is negative, the resultant image is distended in a form suggested by Figure 3.19b; this is referred to as barrel distortion.

Worked Example 3.1The distortion of an optical system is given as a WFE by the expression, 4Φ 0c 3pcosφθ 3, where Φ 0is equal to 50 μm and c = 1. The radius of the pupil, r 0, is 10 mm. What is the distortion, expressed as a deviation in percent from the paraxial angle, at a field angle of 15°? From Eq. (3.12)and when expressed as an angle, the transverse aberration generated is given by:

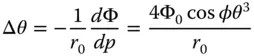
The cosφ term expresses the fact that the direction of the transverse aberration is in the same plane as that of the object/axis. The proportional distortion is therefore given by:

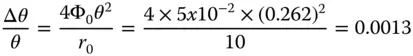
(dimensions in mm; angles in radians)

The proportional distortion is therefore 0.13%.

At this stage it will be useful to summarise the five Gauss-Seidel aberrations in terms of the pupil and field dependence of their OPD and ray fans. It should be noted that for all Gauss-Seidel aberrations, the order of the pupil dependence and the order of the field angle dependence sum to four (for the OPD). In particular, it is important for the reader to understand how the different types of aberration vary with both pupil size and field angle. For example, in many optical systems, such as telescopes and microscopes, the range of field angles tend to be significantly smaller than the larger angles subtended to the pupil. Therefore, for such instruments, those aberrations with a higher-order pupil dependence, such as spherical aberration (4) and coma (3), will predominate.