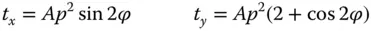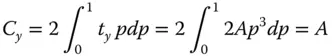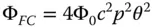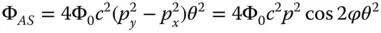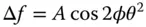To see how these overlapping circles are formed, we introduce an additional angle, the ray fan angle, φ, which describes the angle that the plane of the ray fan makes with respect to the y axis. For the tangential ray fan, this angle is zero. For the sagittal ray fan, this angle is 90°. We can now describe the individual components of the pupil function, p xand p yin terms of the magnitude of the pupil function, p , and the ray fan angle, φ:
(3.26) 
From (3.25)we can express the transverse aberration components in terms of p and φ. This gives:
(3.27) 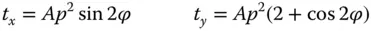
A is a constant
It is clear from Eq. (3.27)that the pattern produced is a series of overlapping circles of radius A√2 p 2offset in y by 2A p 2. Coma is not an aberration that can be ameliorated or balanced by defocus. When analysing transverse aberration, the impact of defocus is to produce an odd (anti-symmetrical) additional contribution with respect to pupil function. The transverse aberration produced by coma, is, of course, even with respect to pupil function, as shown in Figure 3.12. Therefore, any deviation from the paraxial focus will only increase the overall aberration.
Another important consideration with coma is the location of the geometrical spot centroid. This represents the mean ray position at the paraxial focus for an evenly illuminated entrance pupil taken with respect to the chief ray intersection. The centroid locations in x and y, C x, and C y, may be defined as follows.
(3.28) 
By symmetry considerations, the coma centroid is not displaced in x, but it is displaced in y. Integrating over the whole of the pupil function, p (from 0 to 1) and allowing for a weighting proportional to p (the area of each ring), the centroid location in y, Cy may be derived from Eq. (3.27):
(3.29) 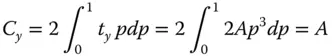
(the term cos2φ is ignored as its average is zero)
So, coma produces a spot centroid that is displaced in proportion to the field angle. The constant A is, of course, proportional to the field angle.
The third Gauss-Seidel term produced is known as field curvature. The OPD associated with field curvature is second order in both field angle and pupil function. Furthermore, there is no dependence upon ray fan angle, as the WFE is circularly symmetric. Unlike in the case for coma, behaviour is identical for the tangential and sagittal ray fans.
(3.30) 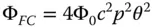
From Eq. (3.30), in the case of a single field point, the effect of a quadratic dependence of WFE on pupil function is to produce a uniform defocus. That is to say, a uniform defocus produces a characteristic quadratic pupil dependence in the WFE. The extent of this defocus is proportional to the square of the field angle, producing a curved surface which intersects the paraxial focal plane at zero field angle – the optical axis. If this field curvature were the only aberration, then this curved surface would produce a perfectly sharp image for all these field points. That is to say, with the presence of field curvature, the ideal focal surface is a curved surface or sphere rather than a plane. This is illustrated in Figure 3.15.
Figure 3.15shows both the tangential and sagittal focal surfaces (S and T), with the optimum focal surface lying between the two. Ideally, for field curvature, the imaging surface should be curved, following the ideal focal surface. If, for instance, only a plane imaging surface is available, then this need not be located at the paraxial focus. This surface can, in principle, be located at an offset, such that the rms WFE is minimised across all fields. In calculating the rms WFE, this would be weighted according to area across all object space, as represented by a circle centred on the optical axis whose radius is the maximum object height.
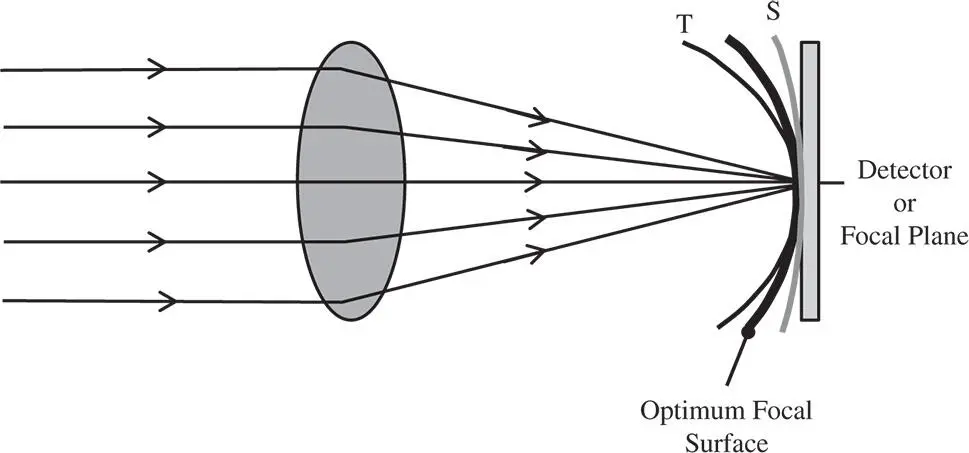
Figure 3.15 Field curvature.
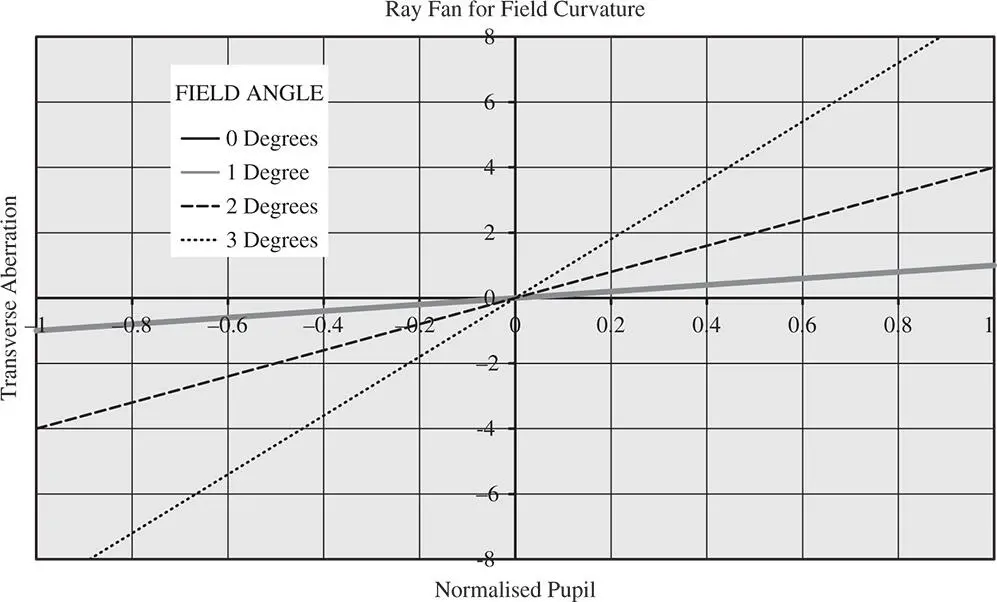
Figure 3.16 Ray fan plots illustrating field curvature.
Clearly, the OPD fan for field curvature is a series of parabolic curves whose height is proportional to the square of the field angle. There is no distinction between the sagittal and tangential fans. Similarly, the ray fans show a series of linear plots whose magnitude is also proportional to the square of the field angle. A series of ray fan plots for field curvature is shown in Figure 3.16.
In view of the symmetry associated with field curvature, the geometrical spot consists of a uniform blur spot whose size increases in proportion to the square of the field angle. In addition, this spot is centred on the chief ray; unlike in the case for coma, there is no centroid shift with respect to the chief ray.
The fourth Gauss-Seidel term produced is known as astigmatism, literally meaning ‘ without a spot ’. Like field curvature, the WFE associated with astigmatism is second order in both field angle and pupil function. It differs from field curvature in that the WFE is non-symmetric and depends upon the ray fan angle as well as the magnitude of the pupil function. That is to say, the behaviour of the tangential and sagittal ray fans is markedly different.
(3.31) 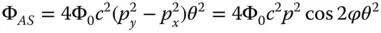
In some respects, the OPD behaviour is similar to field curvature, in that, for a given ray fan, the quadratic dependence upon pupil function implies a uniform defocus. However, the degree of defocus is proportional to cos2φ. Thus, the defocus for the tangential ray fan (cos2φ = 1) and the sagittal ray fan (cos2φ = −1) are equal and opposite. Clearly, the tangential and sagittal foci are separate and displaced and this displacement is proportional to the square of the field angle. The displacement of the ray fan focus is set out in Eq. (3.32):
(3.32) 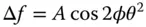
A is a constant
As suggested previously, for a given field angle, the OPD fan would be represented by a series of quadratic curves whose magnitude varies with the ray fan angle. Similarly, the ray fan itself is represented by a series of linear plots whose magnitude is dependent upon the ray fan angle. This is shown in Figure 3.17, which shows the ray fan for a given field angle for both the tangential and sagittal ray fans.
Читать дальше