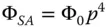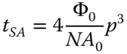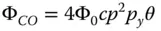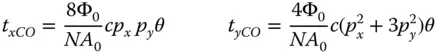Stephen Rolt - Optical Engineering Science

In this section we will describe each of the fundamental third order aberrations in turn. Re-iterating Eq. (3.20)below, it is possible to highlight each of the aberration terms:

We will now describe each of these five terms in turn.

The first term, spherical aberration, has a simple fourth order dependence upon pupil function and no dependence upon field. This is illustrated in Eq. (3.21):

(3.21)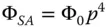

This aberration shows no dependence upon field angle and no dependence upon the orientation of the ray fan. Since, in the current analysis and for a non-zero field angle, the object is offset along the y axis, then the pupil orientation corresponding to p ydefines the tangential ray fan and the pupil orientation corresponding to p xdefines the sagittal ray fan. This is according to the nomenclature set out in Chapter 2. So, the aberration is entirely symmetric and independent of field angle. In fact, the opening discussion in this chapter was based upon an illustration of spherical aberration.

Spherical aberration characteristically produces a circular blur spot. The transverse aberration may, of course, be derived from Eq. (3.21)using Eq. (3.12). For completeness, this is re-iterated below:

(3.22)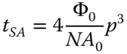

A 2D geometrical plot, of ray intersection at the paraxial focal plane, as produce by an evenly illuminated entrance pupil is referred to as a geometrical point spread function. Due to the symmetry of the aberration, this spot is circular. However, since the transformation in Eq. (3.22)is non-linear, the blur spot associated with spherical aberration is non uniform. For spherical aberration alone (no defocus or other aberrations), the density of the geometrical point spread function is inversely proportional to the pupil function, p . That is to say, spherical aberration manifests itself as a blur spot with a pronounced peak at the centre, with the density declining towards the periphery. This is illustrated in Figure 3.11. The spot, as shown in Figure 3.11, with a pronounced central maximum, is characteristic of spherical aberration and should be recognised as such by the optical designer.

As suggested earlier, the size of this spot can be minimised by moving away from the paraxial focus position. The ray fan and OPD fan for this aberration look like those illustrated in Figures 3.3and 3.8. Overall, the characteristics of spherical aberration and the balancing of this aberration is very much as described in the treatment of generic third order aberration, as set out earlier.

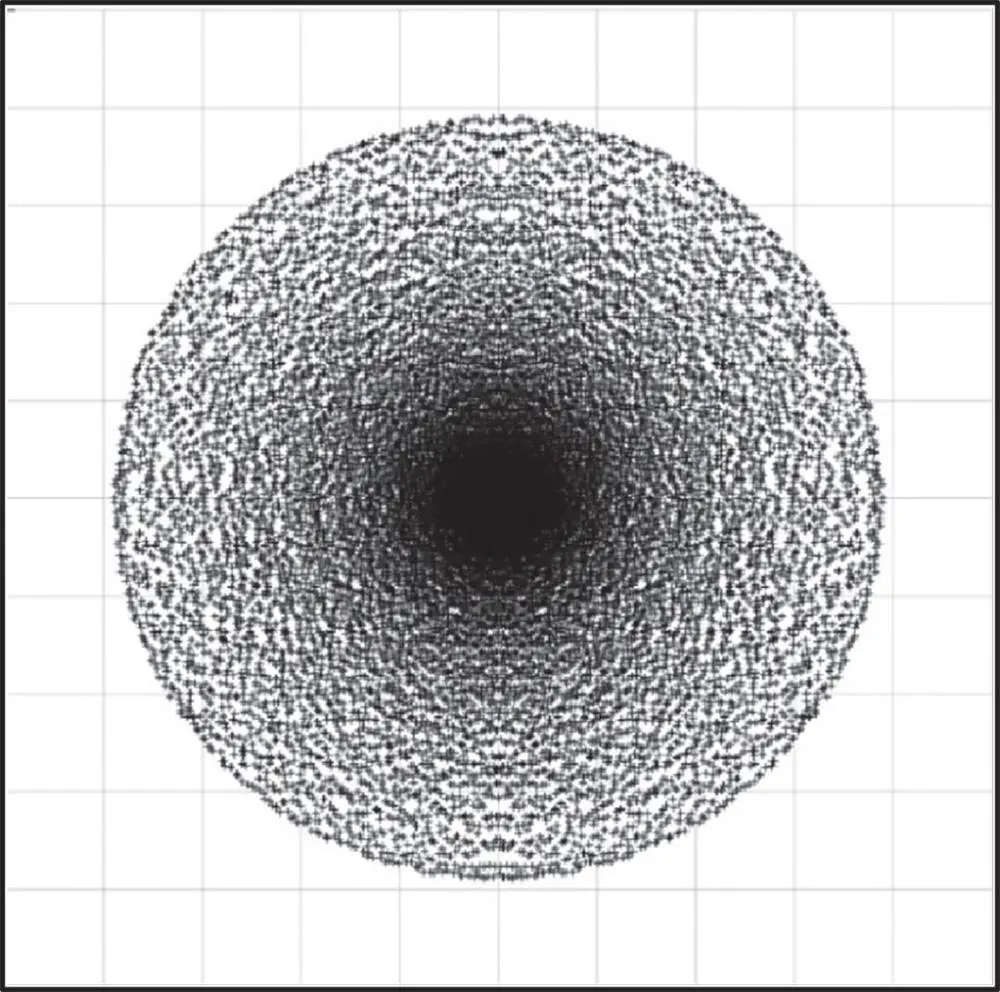
Figure 3.11 Geometrical spot associated with spherical aberration.

The second term, coma, has an WFE that is proportional to the field angle. Its pupil dependence is third order, but it is not symmetrical with respect to the pupil function. The WFE associated with coma is as below:

(3.23)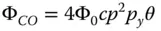

In the preceding discussions, the transverse aberration has been presented as a scalar quantity. This is not strictly true, as the ray position at the paraxial focus is strictly a vector quantity that can only be described completely by an x component, t xand a y component t y. Equation (3.12)should strictly be rendered in the following vectorial form:

(3.24)

The transverse aberration relating to coma may thus be written out as:

(3.25)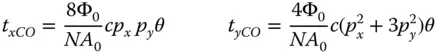

From the perspective of both the OPD and ray fans the behaviour of the tangential (y) and sagittal ray fans are entirely different. As an optical designer, the reader should ultimately be familiar with the form of these fans and learn to recognise the characteristic third order aberrations. For a given field angle, the tangential OPD fan ( p x= 0) shows a cubic dependence upon pupil function, whereas, for the sagittal ray fan ( p y= 0), the OPD is zero. The OPD fan for coma is shown below in Figure 3.12.

The picture for the ray fans is a little more complicated. For both the tangential and sagittal ray fans, there is no component of transverse aberration in the x direction. On the other hand, for both ray fans, there is a quadratic dependence with respect to pupil function for the y component of the transverse aberration. The problem, in essence, it that transverse aberration is a vector quantity. However, when ray fans are computed for optical designs they are presented as scalar plots for each (tangential and sagittal) ray fan. The convention, therefore, is to plot only the y (tangential) component of the aberration in a tangential ray fan, and only the x (sagittal) component of the aberration in a sagittal ray fan. With this convention in mind, the tangential ray fan shows a quadratic variation with respect to pupil function, whereas there is no transverse aberration for the sagittal ray fan. Tangential and sagittal ray fan behaviour is shown in Figure 3.13which shows relevant plots for coma.

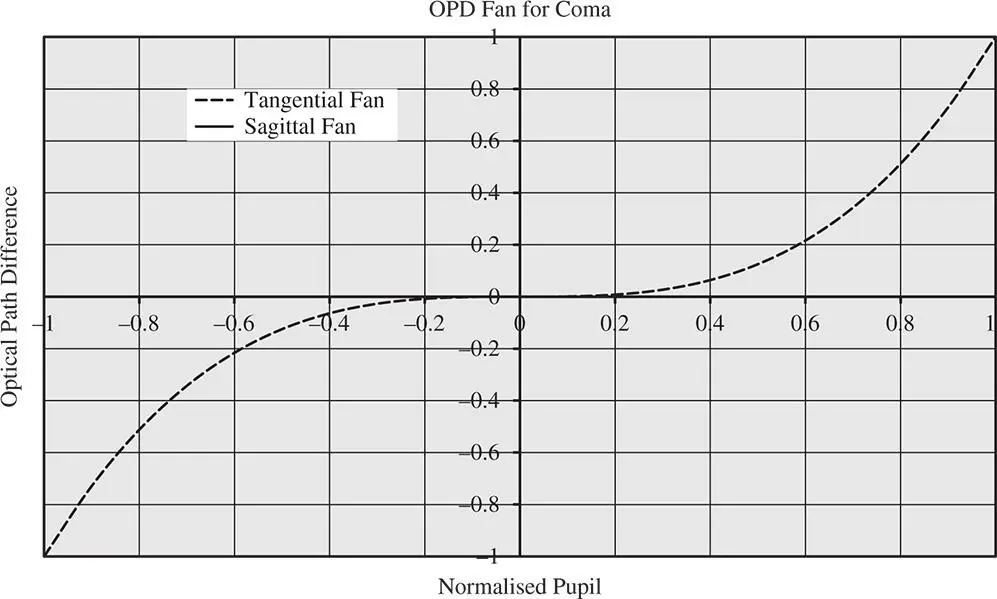
Figure 3.12 OPD fan for coma.

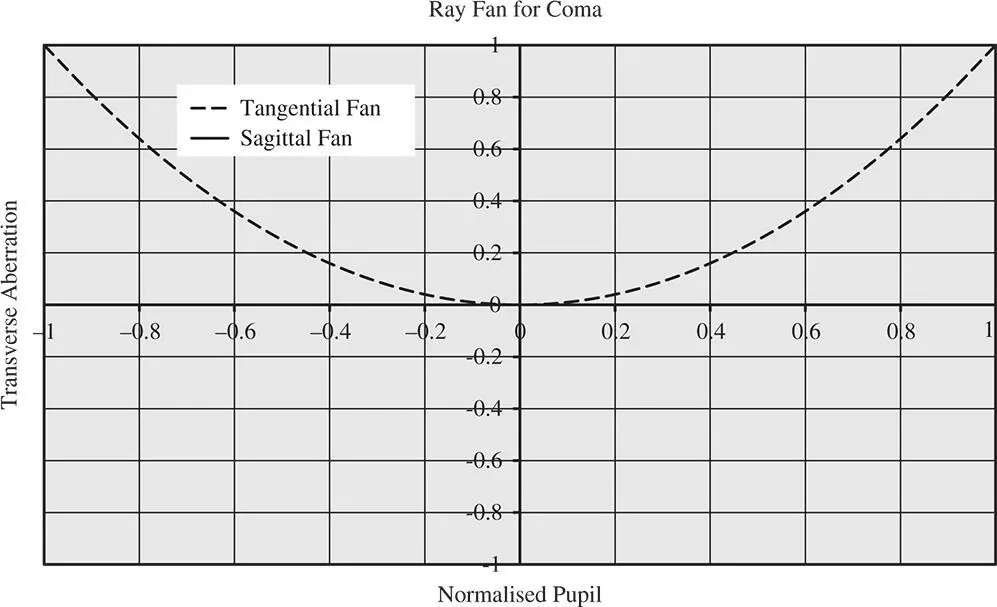
Figure 3.13 Ray fan for coma.

Since the (vector) transverse aberration for coma is non-symmetric, the blur spot relating to coma has a distinct pattern. The blur spot is produced by filling the entrance pupil with an even distribution of rays and plotting their transverse aberration at the paraxial focus. If we imagine the pupil to be composed of a series of concentric rings from the centre to the periphery, these will produce a series of overlapping rings that are displaced in the y direction.

Figure 3.14shows the characteristic geometrical point spread function associated with coma, clearly illustrating the overlapping circles corresponding to successive pupil rings. These overlapping rings produce a characteristic comet tail appearance from which the aberration derives its name. The overlapping circles produce two asymptotes, with a characteristic angle of 60°, as shown in Figure 3.14.

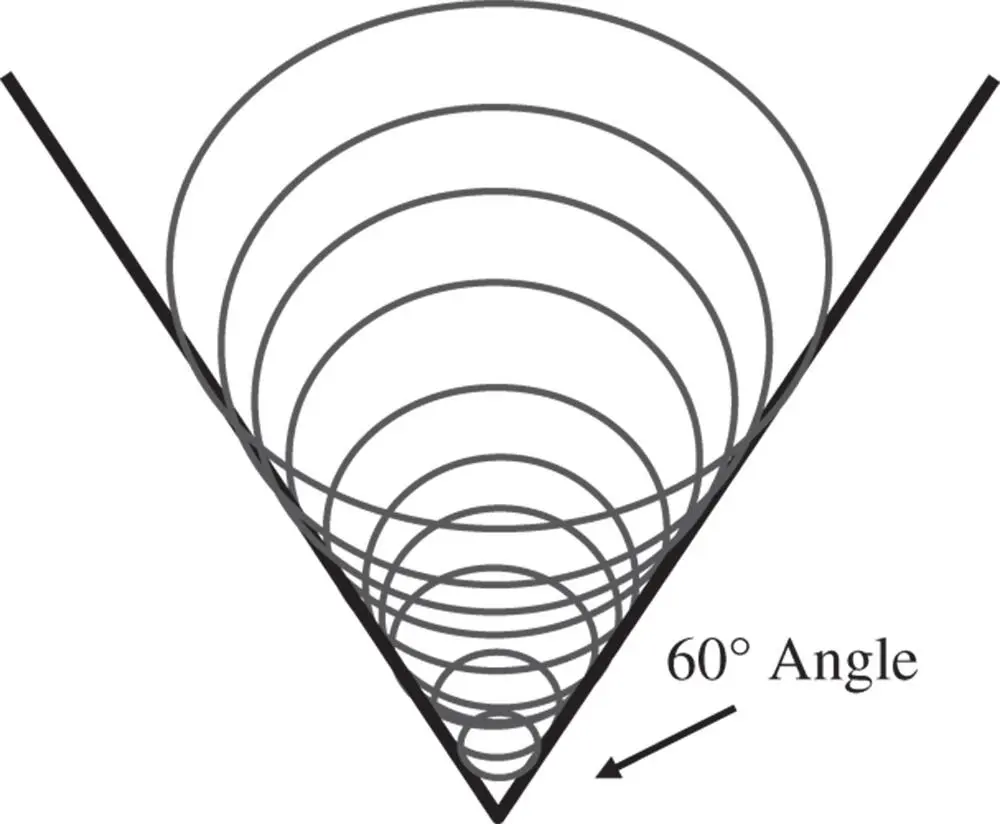
Figure 3.14 Geometrical spot for coma.