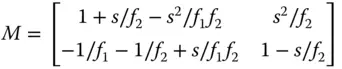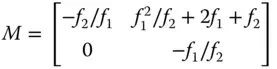Stephen Rolt - Optical Engineering Science

A classical optical telescope is an example of an afocal system. That is to say, no clearly defined focus is presented either in object or image space. As the name suggests, the telescope views distant objects, nominally at the infinite conjugate and provides a collimated output for ocular viewing in the case of a traditional instrument. As far as the instrument is concerned, both object and image are located at the infinite conjugate. Of course, this narrative does assume that the instrument is designed for ocular viewing as opposed to image formation at a detector or photographic plate. In any case, the design principles are similar. Fundamentally, the telescope provides angular magnification of a distant object, and this angular magnification is a key performance attribute.

The basic layout of a simple telescope is shown in Figure 2.9. Light from the distant object is collected by an objective lens whose focal length is f 1and then collimated by an eyepiece with a focal length of f 2. These two lenses are separated by the sum of their focal lengths, thus creating an afocal system with an angular magnification given by the ratio of the lens focal lengths.

The matrix of the telescope is similar to that of the compound microscope, with an objective lens and eyepiece separated by some fixed distance.

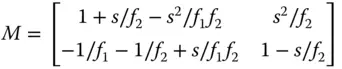
The separation, s, is simply the sum of the two focal lengths and the system matrix is given by:

(2.13)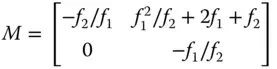

The angular magnification (the D value of the matrix) is simply −f 1/f 2. It is important to note the sign of the magnification, so that for two positive lenses, then the magnification is negative. In line with the previous discussion with regard to the optical invariant, the linear magnification (given by matrix element A) is the inverse of the angular magnification. Also, the C element of the matrix, attesting to the focal power of the system, is actually zero and is characteristic of an afocal system.

As in the case of the microscope, the objective lens forms the system entrance pupil. The exit pupil is formed by the eyepiece imaging the objective lens. This is located a short distance, approximately f 1from the eyepiece, this distance determining the ‘eye relief’. Ideally, for ocular viewing, the pupil of the eye should be co-incident with the exit pupil. Unlike the compound microscope, the exit pupil of a simple (ocular) telescope is relatively large, about the size of the pupil of the eye. Clearly, if the exit pupil were significantly larger than the pupil of the eye, then any light falling outside the ocular pupil would be wasted. In fact, in a typical telescope, where f1 ≫ f2, the size of the exit pupil is approximately given by the diameter of the objective lens multiplied by the ratio of the focal lengths.

As an example, a small astronomical refracting telescope might comprise a 75 mm diameter objective lens with a focal length of 750 mm (f/10) and might use a ×10 eyepiece. Eyepiece magnification is classified in the same way as for microscope eyepieces and so the focal length of this eyepiece would be 25 mm, as derived from Eq. (2.12b). The angular magnification (f 1/f 2) would be ×30 and the size of the pupil about 3 mm, which is smaller than the pupil of the eye.

In the preceding discussion, the basic description of the instrument function assumes ocular viewing, i.e. viewing through an eyepiece. However, increasingly, across a range of optical instruments, the eye is being replaced by a detector chip. This is true of microscope, telescope, and camera instruments.

In essence, the function of a camera is to image an object located at the infinite conjugate and to form an image on a light sensitive planar surface. Of course, traditionally, this light sensitive surface consisted of a film or a plate upon which a silver halide emulsion had been deposited. This allowed the recording of a latent image which could be chemically developed at a later stage. Depending upon the grain size of the silver halide emulsion, feature sizes of around 10–20 μm or so could be resolved. That is to say, the ultimate system resolution is limited by the recording media as well as the optics. For the most part, this photographic film has now been superseded by pixelated silicon detectors, allowing the rapid and automatic capture and processing of images. These detectors are composed of a rectangular array of independent sensor areas (usually themselves rectangular) that each produce a charge in proportion to the amount of light collected. Resolution of these detectors is limited by the pixel size which is analogous to the grain size in photographic film. Pixel size ranges from a one micron to a few microns.

Optically from a paraxial perspective, the camera is an exceptionally simple instrument. Its purpose is simply to image light from an object located at the infinite conjugate onto the focal plane, where the sensor is located. As such, from a system perspective one might regard the camera as a single lens with the sensor located at the second focal point. This is illustrated in Figure 2.10.

If this system is the essence of simplicity, then the Pinhole Camera, a very early form of camera, takes this further by dispensing with the lens altogether! A pinhole camera relies on a very small system aperture (a pinhole) defining the image quality. In this embodiment of the camera, all rays admitted by the entrance pupil follow closely the chief ray. However, light collection efficiency is low. Whilst in the paraxial approximation, the camera presents itself as a very simple instrument, as indeed early cameras were, the demands of light collection efficiency require the use of a large aperture which results in the breakdown of the paraxial approximation. As we shall see in later chapters, this leads to the creation of significant imperfections, or aberrations, in image formation which can only be combatted by complex multi-element lens designs. Thus, in practice, a modern camera, i.e. its lens, is a relatively complex optical instrument.

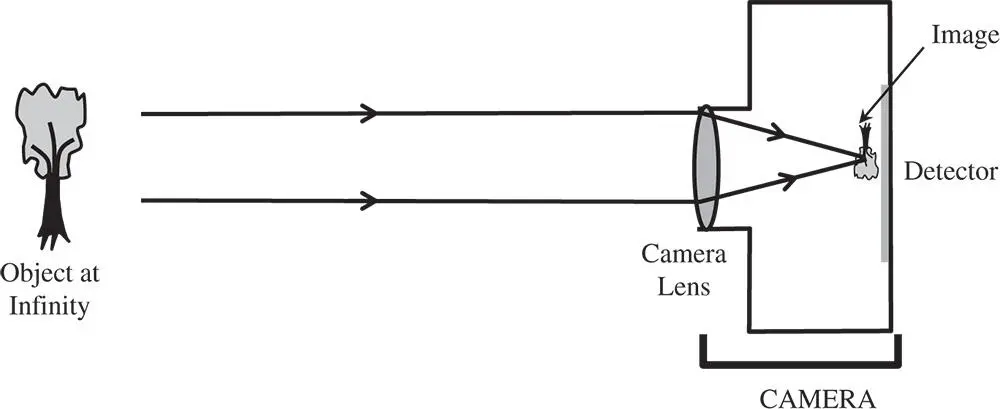
Figure 2.10 Basic camera.

In defining the function of the camera, we spoke of the imaging of an object located at infinity. In this context, ‘infinity’ means a substantially greater object distance than the lens focal length. For the traditional 35 mm format photographic camera, a typical standard lens focal length would be 50 mm. The ‘35 mm’ format refers to the film frame size which was 36 mm × 24 mm (horizontal × vertical). As mentioned in Chapter 1, the focal length of the camera lens determines the ‘plate scale’ of the detector, or the field angle subtended per unit displacement of the detector. Overall, for this example, plate scale is 1.15° mm −1. The total field covered by the frame size is ±20° (Horizontal) × ±13.5° (Vertical). ‘Wide angle’ lenses with a shorter focal length lens (e.g. 28 mm) have a larger plate scale and, naturally a wider field angle. By contrast, telephoto lenses with longer focal lengths (e.g. 200 mm), have a smaller plate scale, thus producing a greater magnification, but a smaller field of view.

Modern cameras with silicon detector technology are generally significantly more compact instruments than traditional cameras. For example, a typical digital camera lens might have a focal length of about 8 mm, whereas a mobile phone camera lens might have a focal length of about half of this. The plate scale of a digital camera is thus considerably larger than that of the traditional camera. Overall, as dictated by the imaging requirements, the field of view of a digital camera is similar to its traditional counterpart, although, in practice, equivalent to that of a wide field lens. Therefore, in view of the shorter focal length, the detector size in a digital camera is considerably smaller than that of a traditional film camera, typically a few mm. Ultimately, the miniaturisation of the digital camera is fundamentally driven by the resolution of the detector, with the pixel size of a mobile phone camera being around 1 μm. This is over an order of magnitude superior to the resolution, or ‘grain size’ of a high specification photographic film.