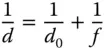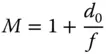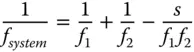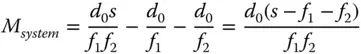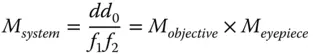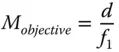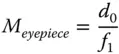Stephen Rolt - Optical Engineering Science

The magnifying glass or eye loupe is perhaps the simplest optical system conceivable, in that is consists of a single lens that is intended to be used with the eye to magnify close objects. Our ability to resolve small, close objects is limited by our ability to focus at close quarters. Typically, although this varies with age and other factors, a comfortable distance for viewing near objects is about 250 mm. If the eye can resolve an angle of 1 arcminute, then this corresponds to a resolution of somewhat under 0.1 mm. Addition of a simple lens allows the eye to view objects at a much shorter distance. This is shown in Figure 2.7.

For the two cases illustrated in Figure 2.7, the eye's focussing power remains the same. Therefore, addition of a lens of focal length f will change the closest approach distance, d 0, to:

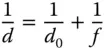
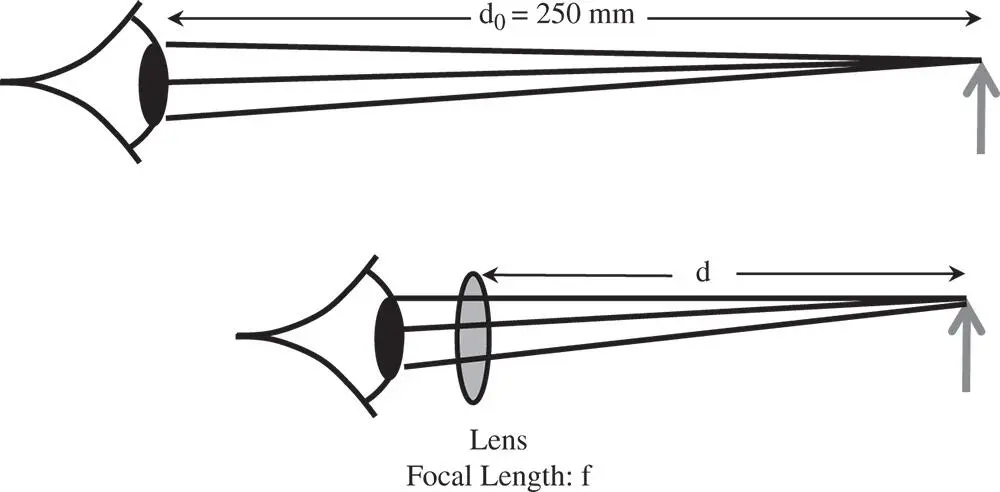
Figure 2.7 Simple magnifying lens.

If the magnification, M, provided by the lens is defined as the ratio of the final image sizes in the two scenarios, the magnification is given by:

(2.8)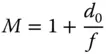

In describing magnifying lenses, as suggested earlier, d 0is defined to be 250 mm. Thus, a lens with a focal length of 250 mm would have a magnification of ×2 and a lens with a focal length of 50 mm would have a magnification of ×6. In practice, simple lenses are only useful up to a magnification of ×10. This is partly because of the introduction of unacceptable aberrations, but also because of the impractical short working distances introduced by lenses with a focal length of a few mm. For higher magnifications, the compound microscope must be used.

Naturally, the pupil of this simple system is defined by the pupil of the eye itself. The size of the eye's pupil varies from about 3 mm in bright light, to about 7 mm under dim lighting conditions, although this varies with individuals.

In the preceding subsection, the limitations of a simple magnifying lens were made clear. Overall, its functionality, in delivering a high magnification, is to convey an intermediate image, located at the infinite conjugate, to the human eye. Furthermore, to provide maximum magnification, the focal length of this lens must be as small as possible. For practical reasons, a magnification of greater than ×10 cannot be delivered. This difficulty is solved by the compound microscope where a two-lens system is used to provide a system focal length that is considerably shorter than would be afforded by a single lens. In essence, a compound microscope consists of two lenses, or lens groups. The first lens is the objective lens that lies close to the object and the second lens, in the traditional microscope, is the eyepiece. Of course, in many modern instruments, the eye is replaced by a pixellated detector chip. Nonetheless the logic followed here still applies. Figure 2.8shows the general set up.

The two lenses are separated by the nominal tube length, d, and an intermediate image is formed by the objective lens within the tube. The eyepiece then presents the final image to the eye at the infinite conjugate. In other words, the intermediate image is designed to be located at a distance f 2(the eyepiece focal length) from the eyepiece. If the objective lens focal length is f 1, then the matrix of the system is:

The entire co-ordinate system is referenced to the position of the objective lens. Of particular relevance here is the first focal length. From the above matrix we have the following equation for the system focal length:

(2.9)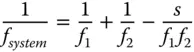

The logic of Eq. (2.9)is that a shorter system focal length can be created than would be reasonably practical with a single lens. Using the same definition as used for the simple magnifying lens, the effective system magnification, M system, is given by the ratio of the closest approach distance d 0, (250 mm), and the system focal length. The system magnification, is given by:

(2.10)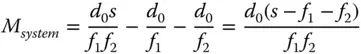

The bracketed quantity, (s − f 1− f 2), i.e. the lens separation minus the sum of the lens focal lengths is known as the optical tube lengthof the microscope, and this will be denoted as d. Generally, for optical microscopes, this tube length is standardised across many commercial instruments with the standard values being 160 or 200 mm. Equation (2.10)may be rewritten as:

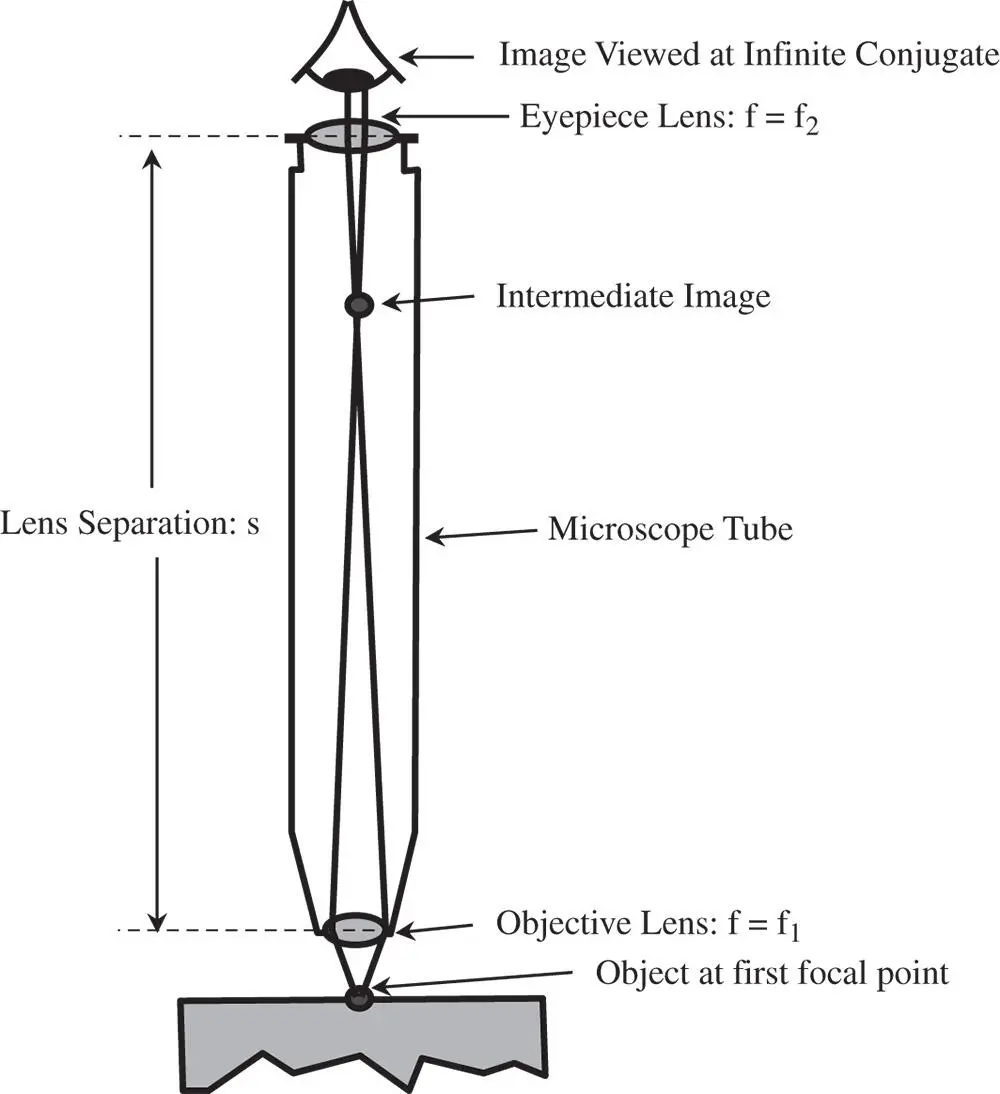
Figure 2.8 Compound microscope.

(2.11)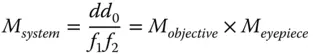

The above formula gives the total magnification of the instrument as the product of the individual magnifications of the objective lens and eyepiece. In this context, these individual magnifications are defined as in Eqs. (2.12a)and (2.12b):

(2.12a)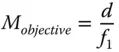

(2.12b)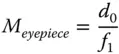

The equations above establish the standard definitions for microscope lens powers. For example, the magnification of microscope objectives is usually in the range of ×10 to ×100. For a standard tube length, d, of 160 mm, this corresponds to an objective focal length ranging from 16 to 1.6 mm. A typical eyepiece, with a magnification of ×10 has a focal length of 25 mm (d 0= 250 mm). By combining a ×100 objective lens with a ×10 eyepiece, a magnification of ×1000 can be achieved. This illustrates the power of the compound microscope.

The entrance pupil is defined by the aperture of the objective lens. This entrance pupil is re-imaged by the eyepiece to create an exit pupil that is close to the eyepiece. Ideally, this should be co-incident with the pupil of the eye. The distance of the exit pupil from final mechanical surface of the eyepiece is known as the eye relief. Placing the exit pupil further away from the physical eyepiece provides greater comfort for the user, hence the term ‘eye relief’. Objective lens aperture tends to be defined by numerical aperture, rather than f-number and range from 0.1 to 1.3 (for oil immersion microscopes).

Figure 2.9 Basic optical telescope.