Since the origin of a coordinate frame is also a point in space, we can assign coordinates that represent the position of the origin of one coordinate frame with respect to another. In Figure 2.1, for example, we may have
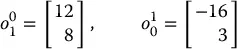
Thus, o 0 1specifies the coordinates of the point o 1relative to frame 0 and o 1 0specifies the coordinates of the point 0 0relative to frame 1. In cases where there is only a single coordinate frame, or in which the reference frame is obvious, we will often omit the superscript. This is a slight abuse of notation, and the reader is advised to bear in mind the difference between the geometric entity called p and any particular coordinate vector that is assigned to represent p . The former is independent of the choice of coordinate frames, while the latter obviously depends on the choice of coordinate frames.
While a point corresponds to a specific location in space, a vectorspecifies a direction and a magnitude. Vectors can be used, for example, to represent displacements or forces. Therefore, while the point p is not equivalent to the vector v 1, the displacement from the origin o 0to the point p is given by the vector v 1. In this text, we will use the term vectorto refer to what are sometimes called free vectors, that is, vectors that are not constrained to be located at a particular point in space. Under this convention, it is clear that points and vectors are not equivalent, since points refer to specific locations in space, but a free vector can be moved to any location in space. Thus, two vectors are equal if they have the same direction and the same magnitude.
When assigning coordinates to vectors, we use the same notational convention that we used when assigning coordinates to points. Thus, v 1and v 2are geometric entities that are invariant with respect to the choice of coordinate frames, but the representation by coordinates of these vectors depends directly on the choice of reference coordinate frame. In the example of Figure 2.1, we would obtain
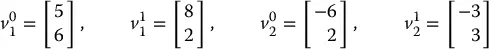
In order to perform algebraic manipulations using coordinates, it is essential that all coordinate vectors be defined with respect to the same coordinate frame. In the case of free vectors, it is enough that they be defined with respect to “parallel” coordinate frames, that is, frames whose respective coordinate axes are parallel, since only their magnitude and direction are specified and not their absolute locations in space.
Using this convention, an expression of the form 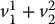 , where
, where 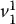 and
and 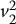 are as in Figure 2.1, is not defined since the frames o 0 x 0 y 0and o 1 x 1 y 1are not parallel. Thus, we see a clear need not only for a representation system that allows points to be expressed with respect to various coordinate frames, but also for a mechanism that allows us to transform the coordinates of points from one coordinate frame to another. Such coordinate transformations are the topic for much of the remainder of this chapter.
are as in Figure 2.1, is not defined since the frames o 0 x 0 y 0and o 1 x 1 y 1are not parallel. Thus, we see a clear need not only for a representation system that allows points to be expressed with respect to various coordinate frames, but also for a mechanism that allows us to transform the coordinates of points from one coordinate frame to another. Such coordinate transformations are the topic for much of the remainder of this chapter.
2.2 Representing Rotations
In order to represent the relative position and orientation of one rigid body with respect to another, we attach coordinate frames to each body, and then specify the geometric relationship between these coordinate frames. In Section 2.1 we saw how one can represent the position of the origin of one frame with respect to another frame. In this section, we address the problem of describing the orientation of one coordinate frame relative to another frame. We begin with the case of rotations in the plane, and then generalize our results to the case of rotations in a three-dimensional space.
2.2.1 Rotation in the Plane
Figure 2.2shows two coordinate frames, with frame o 1 x 1 y 1obtained by rotating frame o 0 x 0 y 0by an angle θ . Perhaps the most obvious way to represent the relative orientation of these two frames is merely to specify the angle of rotation θ . There are two immediate disadvantages to such a representation. First, there is a discontinuity in the mapping from relative orientation to the value of θ in a neighborhood of θ = 0. In particular, for θ = 2 π − ε , small changes in orientation can produce large changes in the value of θ , for example, a rotation by ε causes θ to “wrap around” to zero. Second, this choice of representation does not scale well to the three-dimensional case.
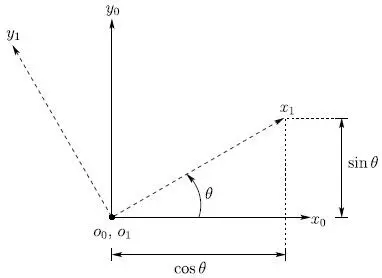
Figure 2.2 Coordinate frame o 1 x 1 y 1is oriented at an angle θ with respect to o 0 x 0 y 0.
A slightly less obvious way to specify the orientation is to specify the coordinate vectors for the axes of frame o 1 x 1 y 1with respect to coordinate frame o 0 x 0 y 0:
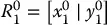
in which 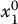 and
and 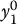 are the coordinates in frame o 0 x 0 y 0of unit vectors x 1and y 1, respectively. 1A matrix in this form is called a rotation matrix. Rotation matrices have a number of special properties that we will discuss below.
are the coordinates in frame o 0 x 0 y 0of unit vectors x 1and y 1, respectively. 1A matrix in this form is called a rotation matrix. Rotation matrices have a number of special properties that we will discuss below.
In the two-dimensional case, it is straightforward to compute the entries of this matrix. As illustrated in Figure 2.2,
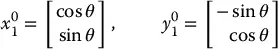
which gives
(2.1) 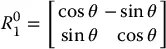
Note that we have continued to use the notational convention of allowing the superscript to denote the reference frame. Thus,  is a matrix whose column vectors are the coordinates of the unit vectors along the axes of frame o 1 x 1 y 1expressed relative to frame o 0 x 0 y 0.
is a matrix whose column vectors are the coordinates of the unit vectors along the axes of frame o 1 x 1 y 1expressed relative to frame o 0 x 0 y 0.
Although we have derived the entries for 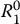 in terms of the angle θ , it is not necessary that we do so. An alternative approach, and one that scales nicely to the three-dimensional case, is to build the rotation matrix by projecting the axes of frame o 1 x 1 y 1onto the coordinate axes of frame o 0 x 0 y 0. Recalling that the dot product of two unit vectors gives the projection of one onto the other, we obtain
in terms of the angle θ , it is not necessary that we do so. An alternative approach, and one that scales nicely to the three-dimensional case, is to build the rotation matrix by projecting the axes of frame o 1 x 1 y 1onto the coordinate axes of frame o 0 x 0 y 0. Recalling that the dot product of two unit vectors gives the projection of one onto the other, we obtain
Читать дальше

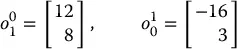
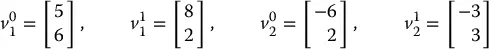
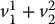 , where
, where 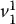 and
and 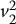 are as in Figure 2.1, is not defined since the frames o 0 x 0 y 0and o 1 x 1 y 1are not parallel. Thus, we see a clear need not only for a representation system that allows points to be expressed with respect to various coordinate frames, but also for a mechanism that allows us to transform the coordinates of points from one coordinate frame to another. Such coordinate transformations are the topic for much of the remainder of this chapter.
are as in Figure 2.1, is not defined since the frames o 0 x 0 y 0and o 1 x 1 y 1are not parallel. Thus, we see a clear need not only for a representation system that allows points to be expressed with respect to various coordinate frames, but also for a mechanism that allows us to transform the coordinates of points from one coordinate frame to another. Such coordinate transformations are the topic for much of the remainder of this chapter.
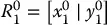
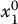 and
and 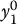 are the coordinates in frame o 0 x 0 y 0of unit vectors x 1and y 1, respectively. 1A matrix in this form is called a rotation matrix. Rotation matrices have a number of special properties that we will discuss below.
are the coordinates in frame o 0 x 0 y 0of unit vectors x 1and y 1, respectively. 1A matrix in this form is called a rotation matrix. Rotation matrices have a number of special properties that we will discuss below.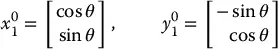
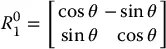
 is a matrix whose column vectors are the coordinates of the unit vectors along the axes of frame o 1 x 1 y 1expressed relative to frame o 0 x 0 y 0.
is a matrix whose column vectors are the coordinates of the unit vectors along the axes of frame o 1 x 1 y 1expressed relative to frame o 0 x 0 y 0.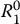 in terms of the angle θ , it is not necessary that we do so. An alternative approach, and one that scales nicely to the three-dimensional case, is to build the rotation matrix by projecting the axes of frame o 1 x 1 y 1onto the coordinate axes of frame o 0 x 0 y 0. Recalling that the dot product of two unit vectors gives the projection of one onto the other, we obtain
in terms of the angle θ , it is not necessary that we do so. An alternative approach, and one that scales nicely to the three-dimensional case, is to build the rotation matrix by projecting the axes of frame o 1 x 1 y 1onto the coordinate axes of frame o 0 x 0 y 0. Recalling that the dot product of two unit vectors gives the projection of one onto the other, we obtain










