1974 — Cincinnati Milacron introduced the T3 robot with computer control.
1975 — Unimation Inc. registers its first financial profit.
1976 — The Remote Center Compliance (RCC) device for part insertion in assembly is developed at Draper Labs in Boston.
1976 — Robot arms are used on the Viking I and II space probes and land on Mars.
1978 — Unimation introduces the PUMA robot, based on designs from a General Motors study.
1979 — The SCARA robot design is introduced in Japan.
1981 — The first direct-drive robot is developed at Carnegie-Mellon University.
1982 — Fanuc of Japan and General Motors form GM Fanuc to market robots in North America.
1983 — Adept Technology is founded and successfully markets the direct-drive robot.
1986 — The underwater robot, Jason, of the Woods Hole Oceanographic Institute, explores the wreck of the Titanic, found a year earlier by Dr. Robert Barnard.
1988 — Stäubli Group purchases Unimation from Westinghouse.
1988 — The IEEE Robotics and Automation Society is formed.
1993 — The experimental robot, ROTEX, of the German Aerospace Agency (DLR) was flown aboard the space shuttle Columbia and performed a variety of tasks under both teleoperated and sensor-based offline programmed modes.
1996 — Honda unveils its Humanoid robot; a project begun in secret in 1986.
1997 — The first robot soccer competition, RoboCup-97, is held in Nagoya, Japan and draws 40 teams from around the world.
1997 — The Sojourner mobile robot travels to Mars aboard NASA’s Mars PathFinder mission.
2001 — Sony begins to mass produce the first household robot, a robot dog named Aibo.
2001 — The Space Station Remote Manipulation System (SSRMS) is launched in space on board the space shuttle Endeavor to facilitate continued construction of the space station.
2001 — The first telesurgery is performed when surgeons in New York perform a laparoscopic gall bladder removal on a woman in Strasbourg, France.
2001 — Robots are used to search for victims at the World Trade Center site after the September 11th tragedy.
2002 — Honda’s Humanoid Robot ASIMO rings the opening bell at the New York Stock Exchange on February 15th.
2004 — The Mars rovers Spirit and Opportunity both landed on the surface of Mars in January of this year. Both rovers far outlived their planned missions of 90 Martian days. Spirit was active until 2010 and Opportunity stayed active until 2018, and holds the record for having driven farther than any off-Earth vehicle in history.
2005 — ROKVISS (Robotic Component Verification on board the International Space Station), the experimental teleoperated arm built by the German Aerospace Center (DLR), undergoes its first tests in space.
2005 — Boston Dynamics releases the quadrupedal robot Big Dog.
2007 — Willow Garage develops the Robot Operating System (ROS).
2011 — Robonaut 2 was launched to the International Space Station.
2017 — A robot called Sophia was granted Saudi Arabian citizenship, becoming the first robot ever to have a nationality.
1 1 See Appendix A.
Part I The Geometry of Robots
A large part of robot kinematics is concerned with establishing various coordinate frames to represent the positions and orientations of rigid objects, and with transformations among these coordinate frames. Indeed, the geometry of three-dimensional space and of rigid motions plays a central role in all aspects of robotic manipulation. In this chapter we study the operations of rotation and translation, and introduce the notion of homogeneous transformations.
Homogeneous transformations combine the operations of rotation and translation into a single matrix multiplication, and are used in Chapter 3to derive the so-called forward kinematic equations of rigid manipulators. Since we make extensive use of elementary matrix theory, the reader may wish to review Appendix B before beginning this chapter.
We begin by examining representations of points and vectors in a Euclidean space equipped with multiple coordinate frames. Following this, we introduce the concept of a rotation matrix to represent relative orientations among coordinate frames. We then combine these two concepts to build homogeneous transformation matrices, which can be used to simultaneously represent the position and orientation of one coordinate frame relative to another. Furthermore, homogeneous transformation matrices can be used to perform coordinate transformations. Such transformations allow us to represent various quantities in different coordinate frames, a facility that we will often exploit in subsequent chapters.
2.1 Representing Positions
Before developing representation schemes for points and vectors, it is instructive to distinguish between the two fundamental approaches to geometric reasoning: the syntheticapproach and the analyticapproach. In the former, one reasons directly about geometric entities (e.g., points or lines), while in the latter, one represents these entities using coordinates or equations, and reasoning is performed via algebraic manipulations. The latter approach requires the choice of a reference coordinate frame. A coordinate frame consists of an origin (a single point in space), and two or three orthogonal coordinate axes, for two- and three-dimensional spaces, respectively.
Consider Figure 2.1, which shows two coordinate frames that differ in orientation by an angle of 45°. Using the synthetic approach, without ever assigning coordinates to points or vectors, one can say that x 0is perpendicular to y 0, or that v 1× v 2defines a vector that is perpendicular to the plane containing v 1and v 2, in this case pointing out of the page.
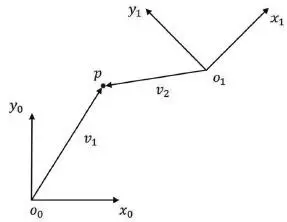
Figure 2.1 Two coordinate frames, a point p , and two vectors v 1and v 2.
In robotics, one typically uses analytic reasoning, since robot tasks are often defined using Cartesian coordinates. Of course, in order to assign coordinates it is necessary to specify a reference coordinate frame. Consider again Figure 2.1. We could specify the coordinates of the point p with respect to either frame o 0 x 0 y 0or frame o 1 x 1 y 1. In the former case we might assign to p the coordinate vector (5, 6) and in the latter case ( − 3, 3). So that the reference frame will always be clear, we will adopt a notation in which a superscript is used to denote the reference frame. Thus, we write
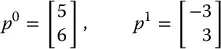
Geometrically, a point corresponds to a specific location in space. We stress here that p is a geometric entity, a point in space, while both 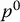 and
and 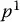 are coordinate vectors that represent the location of this point in space with respect to coordinate frames o 0 x 0 y 0and o 1 x 1 y 1, respectively. When no confusion can arise, we may simply refer to these coordinate frames as frame 0 and frame 1, respectively.
are coordinate vectors that represent the location of this point in space with respect to coordinate frames o 0 x 0 y 0and o 1 x 1 y 1, respectively. When no confusion can arise, we may simply refer to these coordinate frames as frame 0 and frame 1, respectively.
Читать дальше


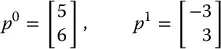
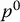 and
and 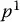 are coordinate vectors that represent the location of this point in space with respect to coordinate frames o 0 x 0 y 0and o 1 x 1 y 1, respectively. When no confusion can arise, we may simply refer to these coordinate frames as frame 0 and frame 1, respectively.
are coordinate vectors that represent the location of this point in space with respect to coordinate frames o 0 x 0 y 0and o 1 x 1 y 1, respectively. When no confusion can arise, we may simply refer to these coordinate frames as frame 0 and frame 1, respectively.










