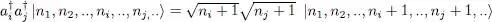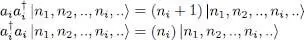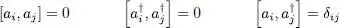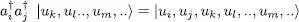or, if initially the state | ui 〉 is not occupied:
(A-26) 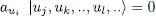
Relations (A-22)and (A-23)are also valid for fermions, with the usual condition that all occupation numbers should be equal to 0 or 1 ; otherwise, the relations amount to 0 = 0.
Comment:
To use relation (A-25)when the state | ui 〉 is already occupied but not listed in the first position, we first have to bring it there; if it requires an odd permutation, a change of sign will occur. For example:
(A-27) 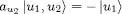
For fermions, the operators a and a †therefore act on the individual state that is listed in the first position in the N -particle ket; a destroys the first state in the list, and at creates a new state placed at the beginning of the list. Forgetting this could lead to errors in sign.
A-4. Occupation number operators (bosons and fermions)
Consider the operator 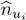 defined by:
defined by:
(A-28) 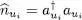
and its action on a Fock state. For bosons, if we apply successively formulas (A-22)and (A-16), we see that this operator yields the same Fock state, but multiplied by its occupation number ni . For fermions, if | ui 〉 is empty in the Fock state, relation (A-26)shows that the action of the operator 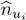 yields zero. If the state | ui 〉 is already occupied, we must first permute the states to bring | ui 〉 to the first position, which may eventually change the sign in front of the Fock space ket. The successive application on this ket of (A-25)and (A-19)shows that the action of the operator
yields zero. If the state | ui 〉 is already occupied, we must first permute the states to bring | ui 〉 to the first position, which may eventually change the sign in front of the Fock space ket. The successive application on this ket of (A-25)and (A-19)shows that the action of the operator 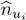 leaves this ket unchanged; we then move the state | ui 〉 back to its initial position, which may introduce a second change in sign, canceling the first one. We finally obtain for fermions the same result as for bosons, except that the ni can only take the values 1 and 0. In both cases the Fock states are the eigenvectors of the operator
leaves this ket unchanged; we then move the state | ui 〉 back to its initial position, which may introduce a second change in sign, canceling the first one. We finally obtain for fermions the same result as for bosons, except that the ni can only take the values 1 and 0. In both cases the Fock states are the eigenvectors of the operator 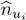 with the occupation numbers as eigenvalues; consequently, this operator is named the “ occupation number operator of the state | ui 〉”. The operator
with the occupation numbers as eigenvalues; consequently, this operator is named the “ occupation number operator of the state | ui 〉”. The operator 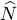 associated with the total number of particles is simply the sum:
associated with the total number of particles is simply the sum:
(A-29) 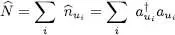
A-5. Commutation and anticommutation relations
Creation and annihilation operators have very simple commutation (for the bosons) and anticommutation (for the fermions) properties, which make them easy tools for taking into account the symmetrization or antisymmetrization of the state vectors.
To simplify the notation, each time the equations refer to a single basis of individual states | ui 〉, we shall write ai instead of aui . If, however, it can lead to ambiguity, we will return to the full notation.
A-5-a. Bosons: commutation relations
Consider, for bosons, the two operators 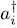 and
and 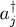 . If both subscripts i and j are different, they correspond to orthogonal states | ui 〉 and | uj 〉. Using twice (A-16)then yields:
. If both subscripts i and j are different, they correspond to orthogonal states | ui 〉 and | uj 〉. Using twice (A-16)then yields:
(A-30) 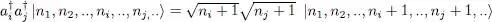
Changing the order of the operators yields the same result. As the Fock states form a basis, we can deduce that the commutator of 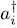 and
and 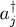 is zero if i ≠ j . In the same way, it is easy to show that both operator products aiaj and ajai acting on the same ket yield the same result (a ket having two occupation numbers lowered by 1); ai and aj thus commute if i ≠ j . Finally the same procedure allows showing that ai and
is zero if i ≠ j . In the same way, it is easy to show that both operator products aiaj and ajai acting on the same ket yield the same result (a ket having two occupation numbers lowered by 1); ai and aj thus commute if i ≠ j . Finally the same procedure allows showing that ai and 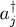 commute if i ≠ j . Now, if i = j , we must evaluate the commutator of ai and
commute if i ≠ j . Now, if i = j , we must evaluate the commutator of ai and 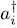 . Let us apply (A-16)and (A-22)successively, first in that order, and then in the reverse order:
. Let us apply (A-16)and (A-22)successively, first in that order, and then in the reverse order:
(A-31) 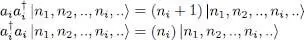
The commutator of ai and 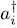 is therefore equal to 1 for all the values of the subscript i . All the previous results are summarized in three equalities valid for bosons:
is therefore equal to 1 for all the values of the subscript i . All the previous results are summarized in three equalities valid for bosons:
(A-32) 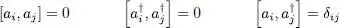
A-5-b. Fermions: anticommutation relations
For fermions, let us first assume that the subscripts i and j are different. The successive action of 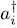 and
and 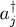 on an occupation number ket only yields a non-zero ket if ni = nj = 0; using twice (A-18)leads to:
on an occupation number ket only yields a non-zero ket if ni = nj = 0; using twice (A-18)leads to:
(A-33) 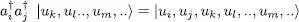
Читать дальше

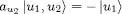
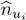 defined by:
defined by: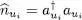
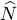 associated with the total number of particles is simply the sum:
associated with the total number of particles is simply the sum: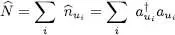
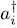 and
and 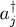 . If both subscripts i and j are different, they correspond to orthogonal states | ui 〉 and | uj 〉. Using twice (A-16)then yields:
. If both subscripts i and j are different, they correspond to orthogonal states | ui 〉 and | uj 〉. Using twice (A-16)then yields: