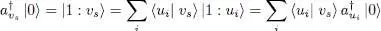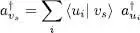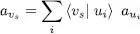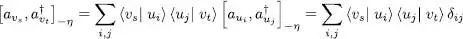but, if we change the order:
(A-34) 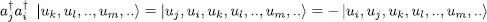
Consequently the sign change that goes with the permutation of the two individual states leads to:
(A-35) 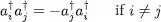
If we define the anticommutator [ A , B ] +of two operators A and B by:
(A-36) 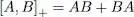
(A-35)may be written as:
(A-37) 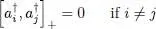
Taking the Hermitian conjugate of (A-35), we get:
(A-38) 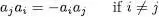
which can be written as:
(A-39) 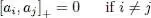
Finally, we show by the same method that the anticommutator of ai and 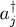 is zero except when it acts on a ket where ni = 1 and nj = 0; those two occupation numbers are then interchanged. The computation goes as follows:
is zero except when it acts on a ket where ni = 1 and nj = 0; those two occupation numbers are then interchanged. The computation goes as follows:
(A-40) 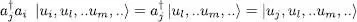
and:
(A-41) 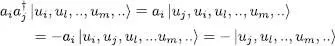
Adding those two equations yields zero, hence proving that the anticommutator is zero:
(A-42) 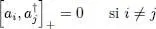
In the case where i = j , the limitation on the occupation numbers (0 or 1) leads to:
(A-43) 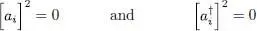
Equalities (A-37)and (A-39)are still valid if i and j are equal. We are now left with the computation of the anticommutator of ai and 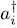 . Let us first examine the product
. Let us first examine the product 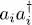 ; it yields zero if applied to a ket having an occupation number ni = 1, but leaves unchanged any ket with ni = 0, since the particle created by
; it yields zero if applied to a ket having an occupation number ni = 1, but leaves unchanged any ket with ni = 0, since the particle created by 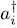 is then annihilated by ai . We get the inverse result for the product
is then annihilated by ai . We get the inverse result for the product 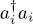 where the order has been inverted: it yields zero if ni = 0, and leaves the ket unchanged if ni = 1. Finally, whatever the occupation number ket is, one of the terms of the anticommutator yields zero, the other 1 , and the net result is always 1 . Therefore:
where the order has been inverted: it yields zero if ni = 0, and leaves the ket unchanged if ni = 1. Finally, whatever the occupation number ket is, one of the terms of the anticommutator yields zero, the other 1 , and the net result is always 1 . Therefore:
(A-44) 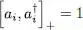
All the previous results valid for fermions are summarized in the following three relations, which are for fermions the equivalent of relations (A-32)for bosons:
(A-45) 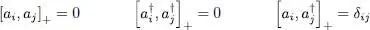
A-5-c. Common relations for bosons and fermions
To regroup the results valid for bosons and fermions in common relations, we introduce the notation:
(A-46) 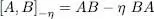
with:
(A-47) 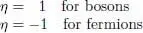
so that (A-46)is the commutator of A and B for bosons, and their anticommutator for fermions. We then have:
(A-48) 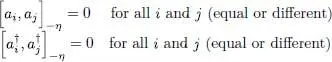
and the only non-zero combinations are:
(A-49) 
What are the effects on the creation and annihilation operators of a change of basis for the individual states? The operators 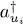 and aui have been introduced by their action on the Fock states, defined by relations (A-7)and (A-10)for which a given basis of individual states {| ui 〉} was chosen. One could also choose any another orthonormal basis {| vs 〉} and define in the same way bases for the Fock state and creation
and aui have been introduced by their action on the Fock states, defined by relations (A-7)and (A-10)for which a given basis of individual states {| ui 〉} was chosen. One could also choose any another orthonormal basis {| vs 〉} and define in the same way bases for the Fock state and creation 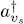 and annihilation avs operators. What is the relation between these new operators and the ones we defined earlier with the initial basis?
and annihilation avs operators. What is the relation between these new operators and the ones we defined earlier with the initial basis?
For creation operators acting on the vacuum state |0〉, the answer is quite straightforward: the action of 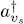 on |0〉 yields a one-particle ket, which can be written as:
on |0〉 yields a one-particle ket, which can be written as:
(A-50) 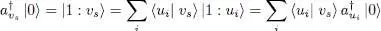
This result leads us to expect a simple linear relation of the type:
(A-51) 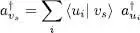
with its Hermitian conjugate:
(A-52) 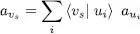
Equation (A-51)implies that creation operators are transformed by the same unitary relation as the individual states. Commutation or anticommutation relations are then conserved, since:
(A-53) 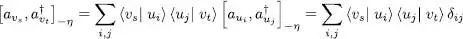
Читать дальше

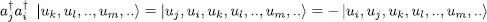
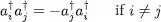
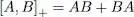
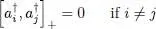
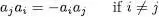
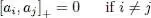
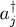 is zero except when it acts on a ket where ni = 1 and nj = 0; those two occupation numbers are then interchanged. The computation goes as follows:
is zero except when it acts on a ket where ni = 1 and nj = 0; those two occupation numbers are then interchanged. The computation goes as follows: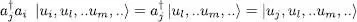
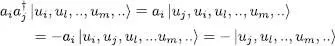
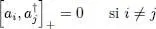
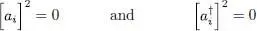
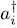 . Let us first examine the product
. Let us first examine the product 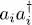 ; it yields zero if applied to a ket having an occupation number ni = 1, but leaves unchanged any ket with ni = 0, since the particle created by
; it yields zero if applied to a ket having an occupation number ni = 1, but leaves unchanged any ket with ni = 0, since the particle created by 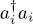 where the order has been inverted: it yields zero if ni = 0, and leaves the ket unchanged if ni = 1. Finally, whatever the occupation number ket is, one of the terms of the anticommutator yields zero, the other 1 , and the net result is always 1 . Therefore:
where the order has been inverted: it yields zero if ni = 0, and leaves the ket unchanged if ni = 1. Finally, whatever the occupation number ket is, one of the terms of the anticommutator yields zero, the other 1 , and the net result is always 1 . Therefore: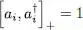
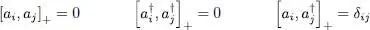
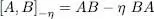
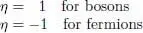
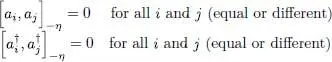

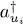 and aui have been introduced by their action on the Fock states, defined by relations (A-7)and (A-10)for which a given basis of individual states {| ui 〉} was chosen. One could also choose any another orthonormal basis {| vs 〉} and define in the same way bases for the Fock state and creation
and aui have been introduced by their action on the Fock states, defined by relations (A-7)and (A-10)for which a given basis of individual states {| ui 〉} was chosen. One could also choose any another orthonormal basis {| vs 〉} and define in the same way bases for the Fock state and creation 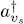 and annihilation avs operators. What is the relation between these new operators and the ones we defined earlier with the initial basis?
and annihilation avs operators. What is the relation between these new operators and the ones we defined earlier with the initial basis?