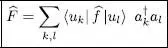B-2. Expression in terms of the operators a and a †
We choose a basis {| ui 〉} for the individual states. The matrix elements fkl of the one-particle operator 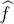 are given by:
are given by:
(B-3) 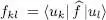
They can be used to expand the operator itself as follows:
(B-4) 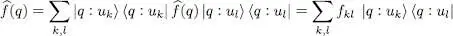
B-2-a. Action of F (N)on a ket with N particles
Using in (B-1)the expression (B-4)for 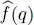 leads to:
leads to:
(B-5) 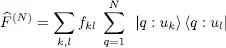
The action of 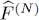 on a symmetrized ket written as (A-9)therefore includes a sum over k and l of terms:
on a symmetrized ket written as (A-9)therefore includes a sum over k and l of terms:
(B-6) 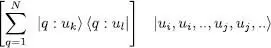
with coefficients fkl . Let us use (A-7)or (A-10)to compute this ket for given values of k and l . As the operator contained in the bracket is symmetric with respect to the exchange of particles, it commutes with the two operators SN and AN (§ C-4-a- β of Chapter XIV)), and the ket can be written as:
(B-7) 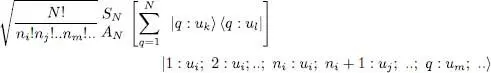
In the summation over q , the only non-zero terms are those for which the individual state | ul 〉 coincides with the individual state | um 〉 occupied in the ket on the right by the particle labeled q; there are nl different values of q that obey this condition (i.e. none or one for fermions). For these nl terms, the operator | q : | uk 〉 〈 q : ul | transforms the state | um 〉 into | ui 〉, then SN (or AN ) reconstructs a symmetrized (but not normalized) ket:
(B-8) 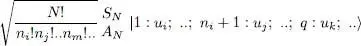
This ket is always the same for all the numbers q among the nl selected ones (for fermions, this term might be zero, if the state | uk 〉 was already occupied in the initial ket). We shall then distinguish two cases:
(i) For k ≠ l , and for bosons, the ket written in (B-8)equals:
(B-9) 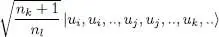
where the square root factor comes from the variation in the occupation numbers nk and nl , which thus change the numerical coefficients in the definition (A-7)of the Fock states. As this ket is obtained nl times, this factor becomes 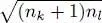 . This is exactly the factor obtained by the action on the same symmetrized ket of the operator
. This is exactly the factor obtained by the action on the same symmetrized ket of the operator 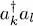 , which also removes a particle from the state | ul 〉 and creates a new one in the state | uk 〉. Consequently, the operator
, which also removes a particle from the state | ul 〉 and creates a new one in the state | uk 〉. Consequently, the operator 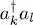 reproduces exactly the same effect as the sum over q .
reproduces exactly the same effect as the sum over q .
For fermions, the result is zero except when, in the initial ket, the state | ul 〉 was occupied by a particle, and the state | uk 〉 empty, in which case no numerical factor appears; as before, this is exactly what the action of the operator 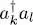 would do.
would do.
(ii) if k = l , for bosons the only numerical factor involved is nl , coming from the number of terms in the sum over q that yields the same symmetrized ket. For fermions, the only condition that yields a non-zero result is for the state | ul 〉 to be occupied, which also leads to the factor nl . In both cases, the sum over q amounts to the action of the operator 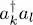 .
.
We have shown that:
(B-10) 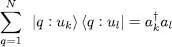
The summation over k and l in (B-5)then yields:
(B-11) 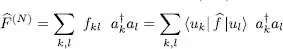
B-2-b. Expression valid in the entire Fock space
The right-hand side of (B-11)contains an expression completely independent of the space S ( N ) or A ( N ) in which we defined the action of the operator 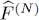 . Since we defined operator
. Since we defined operator 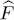 as acting as
as acting as 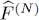 in each of these subspaces having fixed N , we can simply write:
in each of these subspaces having fixed N , we can simply write:
(B-12) 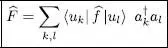
This is the expression of one-particle symmetric operators we were looking for. Its form is valid for any value of N and the particles are no longer numbered; it contains equal numbers of creation and annihilation operators, which only act on occupation numbers.
Comment:
Choosing the proper basis {| ui 〉} it is always possible to diagonalize the Hermitian operator 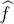 and write:
and write:
Читать дальше

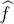 are given by:
are given by: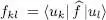
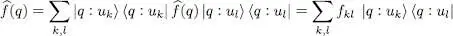
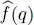 leads to:
leads to: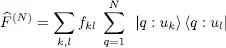
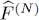 on a symmetrized ket written as (A-9)therefore includes a sum over k and l of terms:
on a symmetrized ket written as (A-9)therefore includes a sum over k and l of terms: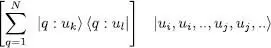
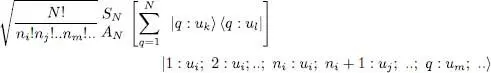
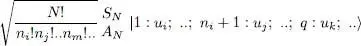
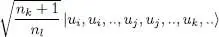
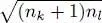 . This is exactly the factor obtained by the action on the same symmetrized ket of the operator
. This is exactly the factor obtained by the action on the same symmetrized ket of the operator 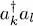 , which also removes a particle from the state | ul 〉 and creates a new one in the state | uk 〉. Consequently, the operator
, which also removes a particle from the state | ul 〉 and creates a new one in the state | uk 〉. Consequently, the operator 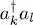 reproduces exactly the same effect as the sum over q .
reproduces exactly the same effect as the sum over q .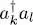 would do.
would do.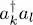 .
.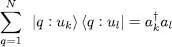
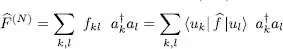
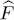 as acting as
as acting as