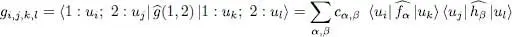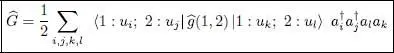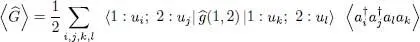(C-1) 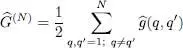
The factor 1/2 present in this expression is arbitrary but often handy. If for example the operator describes an interaction energy that is the sum of the contributions of all the distinct pairs of particles, 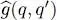 and
and 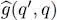 corresponding to the same pair are equal and appear twice in the sum over q and q ′: the factor 1/2 avoids counting them twice. Whenever
corresponding to the same pair are equal and appear twice in the sum over q and q ′: the factor 1/2 avoids counting them twice. Whenever 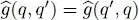 , it is equivalent to write
, it is equivalent to write 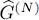 in the form:
in the form:
(C-2) 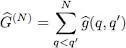
As with the one-particle operators, expression (C-1)defines symmetric operators separately in each physical state’s space having a given particle number N . This definition may be extended to the entire Fock space, which is their direct sum over all N . This results in a more general operator 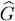 , following the same scheme as for (B-2):
, following the same scheme as for (B-2):
(C-3) 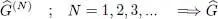
C-2. A simple case: factorization
Let us first assume the operator 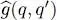 can be factored as:
can be factored as:
(C-4) 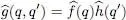
The operator written in (C-1)then becomes:
(C-5) 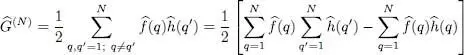
The right-hand side of this expression starts with a product of one-particle operators, each of which can be replaced, following (B-11), by its expression as a function of the creation and annihilation operators:
(C-6) 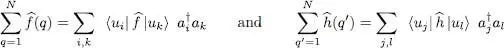
As for the last term on the right-hand side of (C-5), it is already a single particle operator:
(C-7) 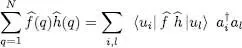
This leads to:
(C-8) 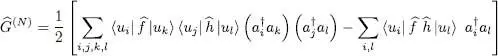
We can then use general relations (A-49)to transform the operator product:
(C-9) 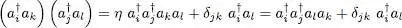
Including this form in the first term on the right-hand side of (C-8)yields, for the δjk contribution:
(C-10) 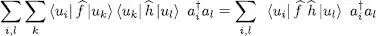
which exactly cancels the second term of (C-8). Consequently, we are left with:
(C-11) 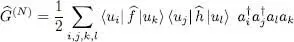
As the right-hand side of this expression has the same form in all spaces having a fixed N , it is also valid for the operator 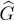 acting in the entire Fock space.
acting in the entire Fock space.
Any two-particle operator 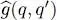 may be decomposed as a sum of products of single particle operators:
may be decomposed as a sum of products of single particle operators:
(C-12) 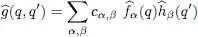
where the coefficients cα, β are numbers 7 . Hence expression (C-1)can be written as:
(C-13) 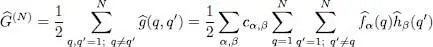
In this linear combination with coefficients cα, β , each term (corresponding to a given α and β ) is of the form (C-5)and can therefore be replaced by expression (C-11). This leads to:
(C-14) 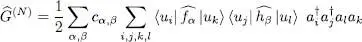
The right-hand side of this equation has the same form in all the spaces of fixed N ; hence it is valid in the entire Fock space. Furthermore, we recognize in the summation over α and β the matrix element of 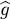 as defined by (C-12):
as defined by (C-12):
(C-15) 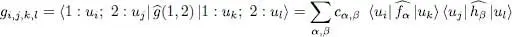
The final result is then:
(C-16) 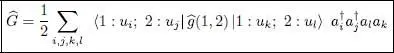
which is the general expression for a two-particle symmetric operator.
As for the one-particle operators, each term of expression (C-16)for the two-particle operators contains equal numbers of creation and annihilation operators. Consequently, these symmetric operators do not change the total number of particles, as was obvious from their initial definition.
C-4. Two-particle reduced density operator
Relation (C-16)implies that the average value of any two-particle operator may be written as:
(C-17) 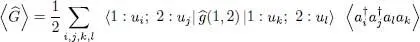
Читать дальше

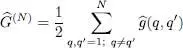
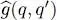 and
and 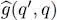 corresponding to the same pair are equal and appear twice in the sum over q and q ′: the factor 1/2 avoids counting them twice. Whenever
corresponding to the same pair are equal and appear twice in the sum over q and q ′: the factor 1/2 avoids counting them twice. Whenever 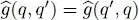 , it is equivalent to write
, it is equivalent to write 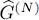 in the form:
in the form: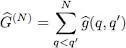
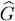 , following the same scheme as for (B-2):
, following the same scheme as for (B-2):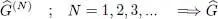
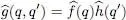
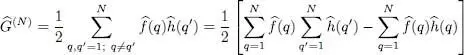
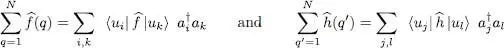
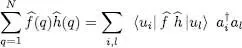
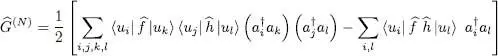
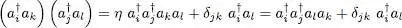
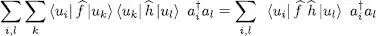
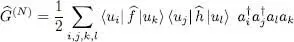
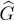 acting in the entire Fock space.
acting in the entire Fock space.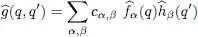
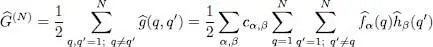
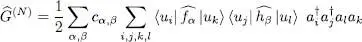
 as defined by (C-12):
as defined by (C-12):