Many physics problems involve computing the average particle interaction energy. For the sake of simplicity, we shall only study here spinless particles (or, equivalently, particles being in the same internal spin state so that the corresponding quantum number does not come into play) and assume their interactions to be binary. These interactions are then described by an operator 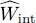 , diagonal in the {| r 1, r 2, … r N〉} basis (eigenstates of all the particles’ positions), which multiplies each of these states by the function:
, diagonal in the {| r 1, r 2, … r N〉} basis (eigenstates of all the particles’ positions), which multiplies each of these states by the function:
(C-25) 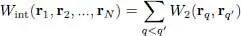
In this expression, the function W 2( r q, r q′) yields the diagonal matrix elements of the operator 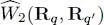 associated with the two-particle ( q , q ′) interaction, where R qis the quantum operator associated with the classical position r q. The matrix elements of this operator in the | uk ; ul 〉 basis is simply obtained by inserting a closure relation for each of the two positions. This leads to:
associated with the two-particle ( q , q ′) interaction, where R qis the quantum operator associated with the classical position r q. The matrix elements of this operator in the | uk ; ul 〉 basis is simply obtained by inserting a closure relation for each of the two positions. This leads to:
(C-26) 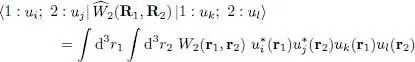
α. General expression:
Replacing in (C-16)operator 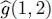 by
by 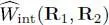 and taking (C-26)into account, we get:
and taking (C-26)into account, we get:
(C-27) 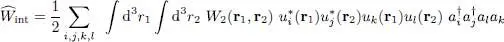
We can thus write the average value of the interaction energy in any normalized state |Φ〉 as:
(C-28) 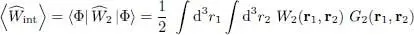
where G 2( r 1, r 2) is the spatial correlation function defined by:
(C-29) 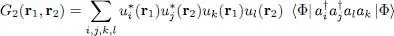
Consequently, knowing the correlation function G 2( r 1, r 2) associated with the quantum state |Φ〉 allows computing directly, by a double spatial integration, the average interaction energy in that state.
Actually, as we shall see in more detail in § B-3 of Chapter XVI, G 2( r 1, r 2) is simply the double density , equal to the probability density of finding any particle in r 1and another one in r 2. The physical interpretation of (C-28)is simple: the average interaction energy is equal to the sum over all the particles’ pairs of the interaction energy W int( r 1, r 2) of a pair, multiplied by the probability of finding such a pair at points r 1and r 2(the factor 1/2 avoids the double counting of each pair).
β. Specific case: the Fock states
Let us assume the state |Φ〉 is a Fock state, with specified occupation numbers ni :
(C-30) 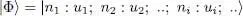
We can compute explicitly, as a function of the ni , the average values:
(C-31) 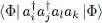
contained in (C-29). We first notice that to get a non-zero result, the two operators a †must create particles in the same states from which they were removed by the two annihilation operators a . Otherwise the action of the four operators on the ket |Φ〉 will yield a new Fock state orthogonal to the initial one, and hence a zero result. We must therefore impose either i = k and j = l , or the opposite i = l and j = k , or eventually the special case where all the subscripts are equal. The first case leads to what we call the “direct term”, and the second, the “exchange term”. We now compute their values.
(i) Direct term, i = k and j = l , shown on the left diagram of Figure 3. If i = j = k = l , the four operators acting on |Φ〉 reconstruct the same ket, multiplied by the factor ni ( ni — 1); this yields a zero result for fermions. If i ≠ j , we can move the operator ak = ai just to the right of the first operator 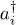 to form the particle number operator
to form the particle number operator 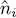 . This permutation in the operators’ order does not change anything: for bosons, we are moving commuting operators, and for fermions, two anticommutations introduce two minus signs, which cancel each other. The same goes for the operators with subscript j , leading to the particle number
. This permutation in the operators’ order does not change anything: for bosons, we are moving commuting operators, and for fermions, two anticommutations introduce two minus signs, which cancel each other. The same goes for the operators with subscript j , leading to the particle number 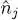 . Finally, the direct term is equal to:
. Finally, the direct term is equal to:
(C-32) 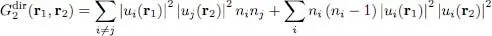
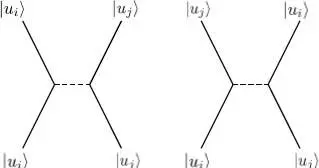
Figure 3: Schematic representation of a direct term (left diagram where each particle remains in the same individual state) and an exchange term (right diagram where the particles exchange their individual states). As in Figure 2, the solid lines represent the particles free propagation, and the dashed lines their binary interaction .
where the second sum is zero for fermions ( ni is equal to 0 or 1).
(ii) Exchange term, i = l and j = k , shown on the right diagram of Figure 3. The case where all four subscripts are equal is already included in the direct term. To get the operators’ product 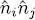 starting from the product
starting from the product 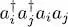 , we just have to permute the two central operators
, we just have to permute the two central operators 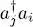 ; when i ≠ j this operation is of no consequence for bosons, but introduces a change of sign for fermions (anticommutation). The exchange term can therefore be written as
; when i ≠ j this operation is of no consequence for bosons, but introduces a change of sign for fermions (anticommutation). The exchange term can therefore be written as 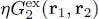 , with:
, with:
Читать дальше

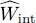 , diagonal in the {| r 1, r 2, … r N〉} basis (eigenstates of all the particles’ positions), which multiplies each of these states by the function:
, diagonal in the {| r 1, r 2, … r N〉} basis (eigenstates of all the particles’ positions), which multiplies each of these states by the function: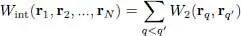
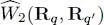 associated with the two-particle ( q , q ′) interaction, where R qis the quantum operator associated with the classical position r q. The matrix elements of this operator in the | uk ; ul 〉 basis is simply obtained by inserting a closure relation for each of the two positions. This leads to:
associated with the two-particle ( q , q ′) interaction, where R qis the quantum operator associated with the classical position r q. The matrix elements of this operator in the | uk ; ul 〉 basis is simply obtained by inserting a closure relation for each of the two positions. This leads to: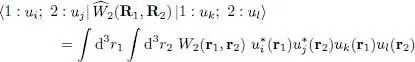
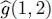 by
by 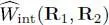 and taking (C-26)into account, we get:
and taking (C-26)into account, we get: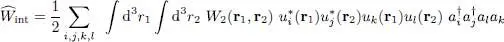
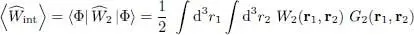
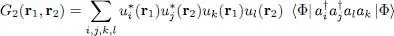
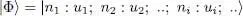
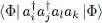
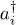 to form the particle number operator
to form the particle number operator 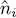 . This permutation in the operators’ order does not change anything: for bosons, we are moving commuting operators, and for fermions, two anticommutations introduce two minus signs, which cancel each other. The same goes for the operators with subscript j , leading to the particle number
. This permutation in the operators’ order does not change anything: for bosons, we are moving commuting operators, and for fermions, two anticommutations introduce two minus signs, which cancel each other. The same goes for the operators with subscript j , leading to the particle number 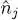 . Finally, the direct term is equal to:
. Finally, the direct term is equal to: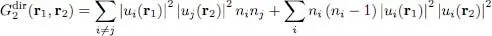

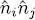 starting from the product
starting from the product 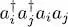 , we just have to permute the two central operators
, we just have to permute the two central operators 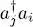 ; when i ≠ j this operation is of no consequence for bosons, but introduces a change of sign for fermions (anticommutation). The exchange term can therefore be written as
; when i ≠ j this operation is of no consequence for bosons, but introduces a change of sign for fermions (anticommutation). The exchange term can therefore be written as 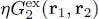 , with:
, with:










