2 2 A commonly accepted but a somewhat illogical expression, since no new quantification comes in addition to that of the usual postulates of Quantum Mechanics; its essential ingredient is the symmetrization of identical particles.
3 3 Remember that, by convention, 0! = 1.
4 4The direct sum of two spaces P (with dimension P) and Q (with dimension Q ) is a space P + Q with dimension P + Q, spanned by all the linear combinations of a vector from the first space with a vector from the second. A basis for P + Q may be simply obtained by grouping together a basis for P and one for Q. For example, vectors of a two-dimensional plane belong to a space that is the direct sum of the one-dimensional spaces for the vectors of two axes of that plane.
5 5A similar notation was used for the harmonic oscillator.
6 6In this relation, the first ps sums are identical, as are the next pt sums, etc.
7 7 The two-particle state space is the tensor product of the two spaces of individual states (see § F-4-b of Chapter II). In the same way, the space of operators acting on two particles is the tensor product of the spaces of operators acting separately on these particles. For example, the operator for the interaction potential between two particles can be decomposed as a sum of products of two operators: the first one is a function of the position of the first particle, and the second one of the position of the second particle.
Complement A XVParticles and holes
1 1 Ground state of a non-interacting fermion gas
2 2 New definition for the creation and annihilation operators
3 3 Vacuum excitations
Creation and annihilation operators are frequently used in solid state physics where the notion of particle and hole plays an important role. A good example is the study of metals or semiconductors, where we talk about an electron-hole pair created by photon absorption. A hole means an absence of a particle, but it has properties similar to a particle, like a mass, a momentum, an energy; the holes obey the same fermion statistics as the electrons they replace. Using creation or annihilation operators allows a better understanding of the hole concept. We will remain in the simple framework of a free particle gas, but the concepts can be generalized to the case of particles placed in an external potential or a Hartree-Fock mean potential (Complement E XV).
1. Ground state of a non-interacting fermion gas
Consider a system of non-interacting fermions in their ground state. We assume for simplicity that they are all in the same spin state, and thus introduce no spin index (generalization to several spin states is fairly simple). As we showed in Complement C XIV, this system in its ground state is described by a state where all the occupation numbers of the individual states having an energy lower than the Fermi energy EF are equal to 1, and all the other individual states are empty. In momentum space, the only occupied states are all the individual states whose wave vector kis included in a sphere (called the “Fermi sphere”) of radius kF (the “Fermi radius”) given by 1 :
(1) 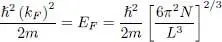
where we have used the notation of formula (7)in Complement C XIV: EF is the Fermi energy (proportional to the particle density to the power 2/3), and L the edge length of the cube containing the N particles. When the system is in its ground state, all the individual states inside the Fermi sphere are occupied, whereas all the other individual states are empty. Choosing for the individual states basis {| ui 〉} the plane wave basis, noted {| uk 〉} to explicit the wave vector k i, the occupation numbers are:
(2) 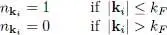
In a macroscopic system, the number of occupied states is very large, of the order of the Avogadro number (≃10 23). The ground state energy is given by:
(3) 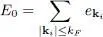
with:
(4) 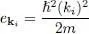
The sum over k iin (3)must be interpreted as a sum over all the k ivalues that obey the boundary conditions in the box of volume L 3, as well as the restriction on the length of the vector k iwhich must be smaller or equal to kF .
2. New definition for the creation and annihilation operators
We now consider this ground state as a new “vacuum” 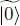 and introduce creation operators that, acting on this vacuum, create excited states for this system. We define:
and introduce creation operators that, acting on this vacuum, create excited states for this system. We define:
(5) 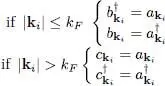
Outside the Fermi sphere, the new operators 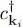 and c kiare therefore simple operators of creation (or annihilation) of a particle in a momentum state that is not occupied in the ground state. Inside the Fermi sphere, the results are just the opposite: operator
and c kiare therefore simple operators of creation (or annihilation) of a particle in a momentum state that is not occupied in the ground state. Inside the Fermi sphere, the results are just the opposite: operator 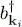 creates a missing particle, that we shall call a “hole”; the adjoint operator b kirepopulates that level, hence destroying the hole. It is easy to show that the anticommutation relations for the new operators are:
creates a missing particle, that we shall call a “hole”; the adjoint operator b kirepopulates that level, hence destroying the hole. It is easy to show that the anticommutation relations for the new operators are:
(6) 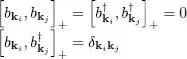
as well as:
(7) 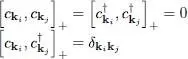
which are the same as for ordinary fermions. Finally, the cross anticommutation relations are:
(8) 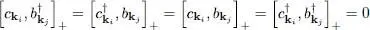
Imagine, for example, that with this new point of view we apply an annihilation operator b ki, with |k i| ≤ kF , to the “new vacuum” 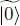 . The result must be zero since it is impossible to annihilate a non-existent hole. From the old point of view and according to (5), this amounts to applying the creation operator
. The result must be zero since it is impossible to annihilate a non-existent hole. From the old point of view and according to (5), this amounts to applying the creation operator 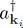 to a system where the individual state |k i〉 is already occupied, and the result is indeed zero, as expected. On the other hand, if we apply the creation operator
to a system where the individual state |k i〉 is already occupied, and the result is indeed zero, as expected. On the other hand, if we apply the creation operator 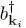 , with |k i| ≤ kF , to the new vacuum, the result is not zero: from the old point of view, it removes a particle from an occupied state, and in the new point of view it creates a hole that did not exist before. The two points of view are consistent.
, with |k i| ≤ kF , to the new vacuum, the result is not zero: from the old point of view, it removes a particle from an occupied state, and in the new point of view it creates a hole that did not exist before. The two points of view are consistent.
Читать дальше

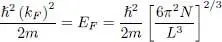
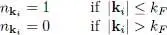
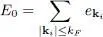
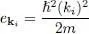
 and introduce creation operators that, acting on this vacuum, create excited states for this system. We define:
and introduce creation operators that, acting on this vacuum, create excited states for this system. We define: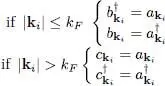
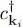 and c kiare therefore simple operators of creation (or annihilation) of a particle in a momentum state that is not occupied in the ground state. Inside the Fermi sphere, the results are just the opposite: operator
and c kiare therefore simple operators of creation (or annihilation) of a particle in a momentum state that is not occupied in the ground state. Inside the Fermi sphere, the results are just the opposite: operator 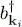 creates a missing particle, that we shall call a “hole”; the adjoint operator b kirepopulates that level, hence destroying the hole. It is easy to show that the anticommutation relations for the new operators are:
creates a missing particle, that we shall call a “hole”; the adjoint operator b kirepopulates that level, hence destroying the hole. It is easy to show that the anticommutation relations for the new operators are: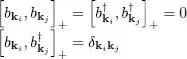
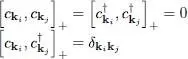
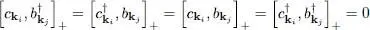
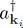 to a system where the individual state |k i〉 is already occupied, and the result is indeed zero, as expected. On the other hand, if we apply the creation operator
to a system where the individual state |k i〉 is already occupied, and the result is indeed zero, as expected. On the other hand, if we apply the creation operator 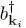 , with |k i| ≤ kF , to the new vacuum, the result is not zero: from the old point of view, it removes a particle from an occupied state, and in the new point of view it creates a hole that did not exist before. The two points of view are consistent.
, with |k i| ≤ kF , to the new vacuum, the result is not zero: from the old point of view, it removes a particle from an occupied state, and in the new point of view it creates a hole that did not exist before. The two points of view are consistent.










