Using relations (42)and (43)of Appendix VI, we can write the grand canonical density operator ρeq (whose trace has been normalized to 1) as:
(1) 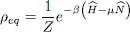
where Z is the grand canonical partition function:
(2) 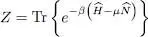
In these relations, β = 1/( kBT ) is the inverse of the absolute temperature T multiplied by the Boltzmann constant kB , and μ , the chemical potential (which may be fixed by a large reservoir of particles). Operators Ĥ and 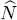 are, respectively, the system Hamiltonian and the particle number operator defined by (B-15) in Chapter XV.
are, respectively, the system Hamiltonian and the particle number operator defined by (B-15) in Chapter XV.
Assuming the particles do not interact, equation (B-1) of Chapter XVallows writing the system Hamiltonian Ĥ as a sum of one-particle operators, in each subspace having a total number of particles equal to N :
(3) 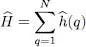
Let us call {| uk 〉} the basis of the individual states that are the eigenstates of the operator 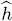 . Noting
. Noting 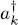 and ak the creation and annihilation operators of a particle in these states, Ĥ may be written as in (B-14):
and ak the creation and annihilation operators of a particle in these states, Ĥ may be written as in (B-14):
(4) 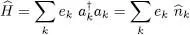
where the ek , are the eigenvalues of 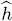 . Operator (1)can also be written as:
. Operator (1)can also be written as:
(5) 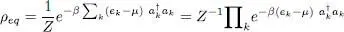
We shall now compute the average values of all the one- or two-particle operators for a system described by the density operator (1).
1-b. Grand canonical partition function, grand potential
In statistical mechanics, the “grand potential” Φ associated with the grand canonical equilibrium is defined as the (natural) logarithm of the partition function, multiplied by - kBT ( cf . Appendix VI, § 1-c β ):
(6) 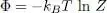
where Z is given by (2). The trace appearing in this equation is easily computed in the basis of the Fock states built from the individual states {| uk 〉}, as we now show. The trace of a tensor product of operators (Chapter II, § F-2-b) is simply the product of the traces of each operator. The Fock space has the structure of a tensor product of the spaces associated with each of the | uk 〉 (each being spanned by kets having a population nk ranging from zero to infinity - see comment (i) of § A-1-c in Chapter XV); we must thus compute a product of traces in each of these spaces. For a fixed k , we sum all the diagonal elements over all the values of nk , then take the product over all k ’s, which leads to:
(7) 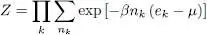
For fermions, as nk can only take the values 0 or 1 (two identical fermions never occupy the same individual state), we get:
(8) 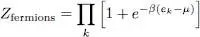
and:
(9) 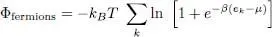
The index k must be summed over all the individual states. In case these states are also labeled by orbital and spin subscripts, these must also be included in the summation. Let us consider for example particles having a spin S and contained in a box of volume 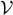 with periodic boundary conditions. The individual stationary states may be written as |k, ν 〉, where kobeys the periodic boundary conditions (Complement C XIV, § 1-c) and the subscript ν takes (2 S + 1) values. Assuming the particles to be free in the box (no spin Hamiltonian), each ν value yields the same contribution to Φ fermions; in the large volume limit, expression (9)then becomes:
with periodic boundary conditions. The individual stationary states may be written as |k, ν 〉, where kobeys the periodic boundary conditions (Complement C XIV, § 1-c) and the subscript ν takes (2 S + 1) values. Assuming the particles to be free in the box (no spin Hamiltonian), each ν value yields the same contribution to Φ fermions; in the large volume limit, expression (9)then becomes:
(10) 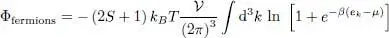
For bosons, the summation over nk in (7)goes from nk = 0 to infinity, which introduces a geometric series whose sum is readily computed. We therefore get:
(11) 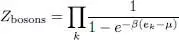
which leads to:
(12) 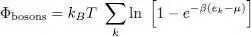
For a system of free particles with spin S , confined in a box with periodic boundary conditions, we obtain, in the large volume limit:
(13) 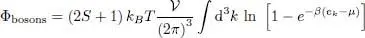
In a general way, for fermions as well as bosons, the grand potential directly yields the pressure P , as shown in relation (61)of Appendix VI:
(14) 
Using the proper derivatives with respect to the equilibrium parameters (temperature, chemical potential, volume), it also yields the other thermodynamic quantities such as the energy, the specific heats, etc.
2. Average values of symmetric one-particle operators
Symmetric quantum operators for one, and then for two particles, were introduced in a general way in Chapter XV(§§ B and C). The general expression for a one-particle operator 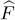 is given by equation (B-12) of that chapter. We can thus write:
is given by equation (B-12) of that chapter. We can thus write:
Читать дальше

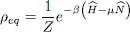
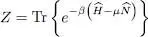
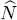 are, respectively, the system Hamiltonian and the particle number operator defined by (B-15) in Chapter XV.
are, respectively, the system Hamiltonian and the particle number operator defined by (B-15) in Chapter XV.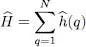
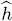 . Noting
. Noting 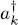 and ak the creation and annihilation operators of a particle in these states, Ĥ may be written as in (B-14):
and ak the creation and annihilation operators of a particle in these states, Ĥ may be written as in (B-14):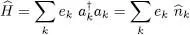
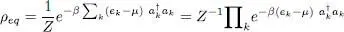
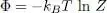
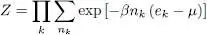
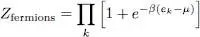
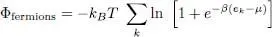
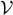 with periodic boundary conditions. The individual stationary states may be written as |k, ν 〉, where kobeys the periodic boundary conditions (Complement C XIV, § 1-c) and the subscript ν takes (2 S + 1) values. Assuming the particles to be free in the box (no spin Hamiltonian), each ν value yields the same contribution to Φ fermions; in the large volume limit, expression (9)then becomes:
with periodic boundary conditions. The individual stationary states may be written as |k, ν 〉, where kobeys the periodic boundary conditions (Complement C XIV, § 1-c) and the subscript ν takes (2 S + 1) values. Assuming the particles to be free in the box (no spin Hamiltonian), each ν value yields the same contribution to Φ fermions; in the large volume limit, expression (9)then becomes: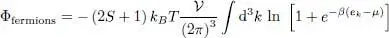
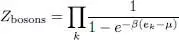
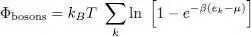
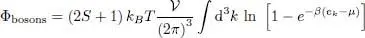

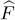 is given by equation (B-12) of that chapter. We can thus write:
is given by equation (B-12) of that chapter. We can thus write:










