The first order derivative term yields:
(38) 
and the second order derivative term is:
(39) 
Summing these two terms yields:
(40) 
Multiplying by 1/[1 — e –β (ei – μ)] the product at the end of the right-hand side of (36)yields the partition function Z , which cancels out the first factor 1/ Z . We are then left with:
(41) 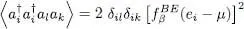
This result proves that (35)remains valid even in the case i = j .
β. Physical discussion: occupation number fluctuations
For two different physical states i and j , the average value 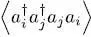 for an ideal gas is simply equal to the product of the average values
for an ideal gas is simply equal to the product of the average values 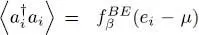 and
and 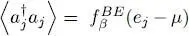 ; this is a consequence of the total absence of interaction between the particles. The same is true for the average value
; this is a consequence of the total absence of interaction between the particles. The same is true for the average value 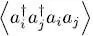 .
.
Now if i = j , we note the factor 2 in relation (41). As we now show, this factor leads to the presence of strong fluctuations associated with the operator 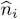 , the particle number in the state
, the particle number in the state 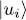 . The calculations shows that:
. The calculations shows that:
(42a) 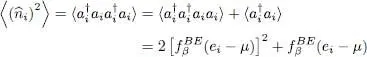
The square of the root mean square deviation Δ ni , is therefore given by:
(42b) 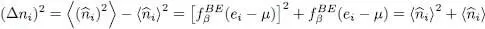
The fluctuations of this operator are therefore larger than its average value, which implies that the population of each state | ui 〉 is necessarily poorly defined 1 at thermal equilibrium. This is particularly true for large 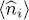 : in an ideal boson gas, a largely populated individual state is associated with a very large population fluctuation. This is due to the shape of the Bose-Einstein distribution (24), a decreasing exponential which is maximum at the origin: the most probable occupation number is always ni = 0. Hence it is impossible to get a very large average
: in an ideal boson gas, a largely populated individual state is associated with a very large population fluctuation. This is due to the shape of the Bose-Einstein distribution (24), a decreasing exponential which is maximum at the origin: the most probable occupation number is always ni = 0. Hence it is impossible to get a very large average 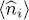 without introducing a distribution spreading over many ni values. Complement H XV(§ 4-a) discusses certain consequences of these fluctuations for an ideal gas. It also shows that as soon as a weak repulsive particle interaction is introduced, the fluctuations greatly diminish and almost completely disappear, since their presence would lead to a very large increase in the potential energy.
without introducing a distribution spreading over many ni values. Complement H XV(§ 4-a) discusses certain consequences of these fluctuations for an ideal gas. It also shows that as soon as a weak repulsive particle interaction is introduced, the fluctuations greatly diminish and almost completely disappear, since their presence would lead to a very large increase in the potential energy.
To summarize, we can write in all cases:
(43) 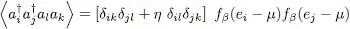
with:
(44) 
As shown in relation (C-19) of Chapter XV, this average value is simply the matrix element 〈1 : uk ; 2 : ul  1 : ui ; 2 : uj 〉 of the two-particle reduced density operator. To get the general expression for the average of any symmetric two-particle operator, we simply use (43)in (28). Consequently, for independent particles, the average values of all these operators are simply expressed in terms of the quantum Fermi-Dirac and Bose-Einstein distribution functions.
1 : ui ; 2 : uj 〉 of the two-particle reduced density operator. To get the general expression for the average of any symmetric two-particle operator, we simply use (43)in (28). Consequently, for independent particles, the average values of all these operators are simply expressed in terms of the quantum Fermi-Dirac and Bose-Einstein distribution functions.
Complement C XVIwill show how the Wick theorem allows generalizing these results to operators dealing with any number of particles.
4. Total number of particles
The operator  corresponding to the total number of particles is given by the sum over all the individual states:
corresponding to the total number of particles is given by the sum over all the individual states:
(45) 
and its average value is given by:
(46) 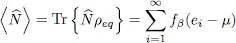
As fβ increases as a function of μ , the total number of particles is controlled (for fixed β ) by the chemical potential.
For the sake of simplicity, we study the ideal gas properties without taking into account the spin, which assumes that all particles are in the same spin state (the spin can easily be accounted for by adding the contributions of the different individual spin states). For a large physical system, the energy levels are very close and the discrete sum in (46)can be replaced by an integral. This leads to:
(47) 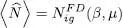
where the function 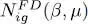 is defined as (the subscript ig stands for ideal gas):
is defined as (the subscript ig stands for ideal gas):
(48) 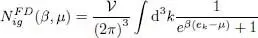
Читать дальше

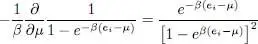
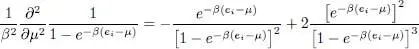
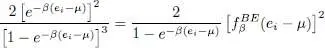
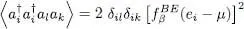
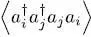 for an ideal gas is simply equal to the product of the average values
for an ideal gas is simply equal to the product of the average values 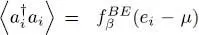 and
and 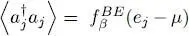 ; this is a consequence of the total absence of interaction between the particles. The same is true for the average value
; this is a consequence of the total absence of interaction between the particles. The same is true for the average value 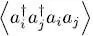 .
.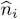 , the particle number in the state
, the particle number in the state 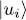 . The calculations shows that:
. The calculations shows that: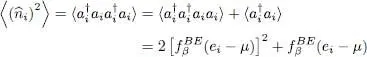
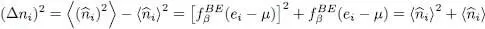
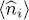 : in an ideal boson gas, a largely populated individual state is associated with a very large population fluctuation. This is due to the shape of the Bose-Einstein distribution (24), a decreasing exponential which is maximum at the origin: the most probable occupation number is always ni = 0. Hence it is impossible to get a very large average
: in an ideal boson gas, a largely populated individual state is associated with a very large population fluctuation. This is due to the shape of the Bose-Einstein distribution (24), a decreasing exponential which is maximum at the origin: the most probable occupation number is always ni = 0. Hence it is impossible to get a very large average 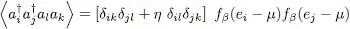
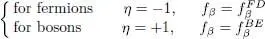
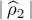 1 : ui ; 2 : uj 〉 of the two-particle reduced density operator. To get the general expression for the average of any symmetric two-particle operator, we simply use (43)in (28). Consequently, for independent particles, the average values of all these operators are simply expressed in terms of the quantum Fermi-Dirac and Bose-Einstein distribution functions.
1 : ui ; 2 : uj 〉 of the two-particle reduced density operator. To get the general expression for the average of any symmetric two-particle operator, we simply use (43)in (28). Consequently, for independent particles, the average values of all these operators are simply expressed in terms of the quantum Fermi-Dirac and Bose-Einstein distribution functions.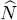 corresponding to the total number of particles is given by the sum over all the individual states:
corresponding to the total number of particles is given by the sum over all the individual states: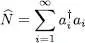
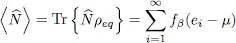
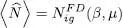
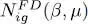 is defined as (the subscript ig stands for ideal gas):
is defined as (the subscript ig stands for ideal gas):