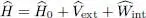The pressure of an ideal boson gas is derived from the grand potential (12), taking into account its relation (14)to the pressure P and volume 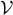 :
:
(71) 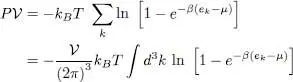
(the second relation being valid in the limit of large volumes). This leads to:
(72) 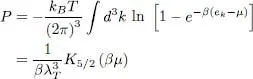
with:
(73) 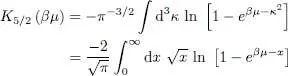
As μ → 0, the contribution P 0of the ground level to the pressure written in (71)is:
(74) 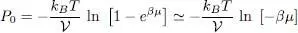
When the chemical potential tends towards zero as in (66), it leads to:
(75) 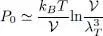
which therefore goes to zero in the limit of large volumes. For a large system, the ground level contribution to the pressure remains negligible compared to that of all the other individual energy levels, whose number gets bigger as the system gets larger. Contrary to what we encountered for the average total particle number, the condensed particles’ contribution to the pressure goes to zero in the limit of large volumes.
As we have seen for fermions, the equation of state must be obtained by eliminating the chemical potential μ between equations (72)yielding the pressure and (65)yielding the total particle number. As opposed to an ideal fermion gas, whose particle number and pressure increase without limit as μ and the density increase, the pressure in a boson system is limited. As soon as the system condenses, only the particle number in the individual ground state continues to grow, but not the pressure. In other words, the physical system acquires an infinite compressibility, and becomes a “marginally pathological” system (a system whose pressure decreases with its volume is unstable). This pathology comes, however, from totally neglecting the bosons’ interactions. As soon as repulsive interactions are introduced, no matter how small, the compressibility will take on a finite value and the pathology will disappear.
This complement is a nice illustration of the simplifications incurred by the systematic use, in the calculations, of the creation and annihilation operators. We shall see in the following complements that these simplifications still occur when taking into account the interactions, provided we stay in the framework of the mean field approximation. Complement B XVIwill even show that for an interacting system studied without using this approximation, the ideal gas distribution functions are still somewhat useful for expressing the average values of various physical quantities.
1 1 A physical observable is said to have a well defined value in a given quantum state if, in this state, its root mean square deviation is small compared to its average value.
2 2 The subscript 3/2 refers to the subscript used for more general functions fm (z), often called the Fermi functions in physics. They are defined by , where z is the “fugacity” z = eβμ. Expanding in terms of z the function 1/[1 + z–1 ex] = ze–x/[1 + ze–x] and using the properties of the Euler Gamma function, it can be shown that I3/2(βμ) = f3/2(z).
3 3 Defining other boundary conditions on the box walls will lead in general to a non-zero ground state energy; choosing that value as the common origin for the energies and the chemical potential will leave the following computations unchanged.
4 4 The subscript 3/2 refers to the subscript used for the functions gm(z), often called, in physics, the Bose functions (or the polylogarithmic functions). They are defined by the series . The exact value of the number ζ defined in (61)is thus given by the series .
5 5 The limit where while the density remains constant is often called the “thermodynamic limit”.
6 6 As above, we assume periodic conditions on the box walls. Another choice would be to impose zero values for the wave functions on the walls: the numerical coefficients of the individual energies would be changed, but not the line of reasoning.
Complement C XVCondensed boson system, Gross-Pitaevskii equation
1 1 Notation, variational ket 1-a Hamiltonian 1-b Choice of the variational ket (or trial ket)
2 2 First approach 2-a Trial wave function for spinless bosons, average energy 2-b Variational optimization
3 3 Generalization, Dirac notation 3-a Average energy 3-b Energy minimization 3-c Gross-Pitaevskii equation
4 4 Physical discussion 4-a Energy and chemical potential 4-b Healing length 4-c Another trial ket: fragmentation of the condensate
The Bose-Einstein condensation phenomenon for an ideal gas (no interaction) of N identical bosons was introduced in § 4-b- β of Complement B XV. We show in the present complement how to describe this phenomenon when the bosons interact. We shall look for the ground state of this physical system within the mean field approximation, using a variational method (see Complement E XI). After introducing in § 1 the notation and the variational ket, we study in § 2 spinless bosons, for which the wave function formalism is simple and the introduction of the creation and annihilation operators does not lead to any major computation simplifications. This will lead us to a first version of the Gross-Pitaevskii equation. We will then come back in § 3 to Dirac notation and the creation operators, to deal with the more general case where each particle may have a spin. Defining the Gross-Pitaevskii potential operator, we shall obtain a more general version of that equation. Finally, some properties of the Gross-Pitaevskii equation will be discussed in § 4, as well as the role of the chemical potential, the existence of a relaxation (or “healing”) length, and the energetic consequences of “condensate fragmentation” (these terms will be defined in § 4-c).
1. Notation, variational ket
We first define the notation and the variational family of state vectors that will lead to relatively simple calculations for a system of identical interacting bosons.
The Hamiltonian operator Ĥ we consider is the sum of operators for the kinetic energy 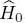 , the one-body potential energy
, the one-body potential energy 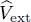 , and the interaction energy
, and the interaction energy 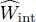 :
:
(1) 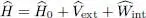
Читать дальше

 :
: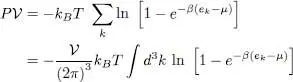
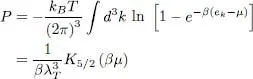
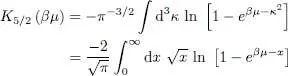
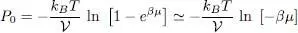
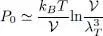
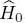 , the one-body potential energy
, the one-body potential energy 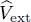 , and the interaction energy
, and the interaction energy 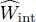 :
: