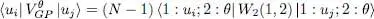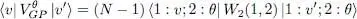As already mentioned, we shall see in § 4-a that μ is simply the chemical potential.
3. Generalization, Dirac notation
We now go back to the previous line of reasoning, but in a more general case where the bosons may have spins. The variational family is the set of the N -particle state vectors written in (7). The one-body potential may depend on the position r, and, at the same time, act on the spin (particles in a magnetic field gradient, for example).
To compute the average energy value  , we use a basis {| θ k〉} of the individual state space, whose first vector is | θ 1〉 = | θ 〉.
, we use a basis {| θ k〉} of the individual state space, whose first vector is | θ 1〉 = | θ 〉.
Using relation (B-12) of Chapter XV, we can write the average value 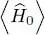 as:
as:
(29) 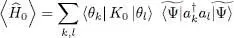
Since 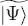 is a Fock state whose only non-zero population is that of the state | θ 1〉, the ket
is a Fock state whose only non-zero population is that of the state | θ 1〉, the ket  is non-zero only if l = 1; it is then orthogonal to
is non-zero only if l = 1; it is then orthogonal to 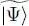 if k ≠ 1. Consequently, the only term left in the summation corresponds to k = l = 1. As the operator
if k ≠ 1. Consequently, the only term left in the summation corresponds to k = l = 1. As the operator 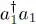 multiplies the ket by its population N , we get:
multiplies the ket by its population N , we get:
(30) 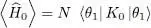
With the same argument, we can write:
(31) 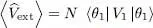
Using relation (C-16) of Chapter XV, we can express the average value of the interaction energy as 3 :
(32) 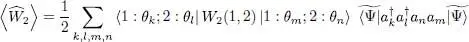
In this case, for the second matrix element to be non-zero, both subscripts m and n must be equal to 1 and the same is true for both subscripts k and l (otherwise the operator will yield a Fock state orthogonal to 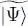 ). When all the subscripts are equal to 1, the operator multiplies the ket
). When all the subscripts are equal to 1, the operator multiplies the ket 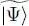 by N ( N — 1). This leads to:
by N ( N — 1). This leads to:
(33) 
The average interaction energy is therefore simply the product of the number of pairs N ( N —1)/2 that can be formed with N particles and the average interaction energy of a given pair.
We can replace | θ 1〉 by | θ 〉, since they are equal. The variational energy, obtained as the sum of (30), (31)and (33), then reads:
(34) 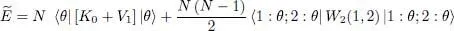
Consider a variation of | θ 〉:
(35) 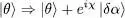
where | δα 〉 is an arbitrary infinitesimal ket of the individual state space, and χ an arbitrary real number. To ensure that the normalization condition (6)is still satisfied, we impose | δα 〉 and | θ 〉 to be orthogonal:
(36) 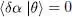
so that 〈 θ | θ 〉 remains equal to 1 (to the first order in | δα 〉). Inserting (35)into (34)to obtain the variation  of the variational energy, we get the sum of two terms: the first one comes from the variation of the ket | θ 〉 and is proportional to eiχ the second one comes from the variation of the bra 〈 θ | and is proportional to e–χ . The result has the form:
of the variational energy, we get the sum of two terms: the first one comes from the variation of the ket | θ 〉 and is proportional to eiχ the second one comes from the variation of the bra 〈 θ | and is proportional to e–χ . The result has the form:
(37) 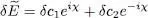
The stationarity condition for 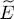 must hold for any arbitrary real value of χ . As before (§ 2-b- α ), it follows that both δc 1and δc 2are zero. Consequently, we can impose the variation
must hold for any arbitrary real value of χ . As before (§ 2-b- α ), it follows that both δc 1and δc 2are zero. Consequently, we can impose the variation 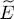 to be zero as just the bra 〈 ι | varies (but not the ket | θ 〉), or the opposite.
to be zero as just the bra 〈 ι | varies (but not the ket | θ 〉), or the opposite.
Varying only the bra, we get the condition:
(38) 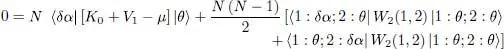
As the interaction operator W 2(1, 2) is symmetric, the last two terms within the bracket in this equation are equal. We get (after simplification by N ):
(39) 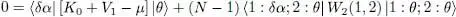
3-c. Gross-Pitaevskii equation
To deal with equation (39), we introduce the Gross-Pitaevskii operator 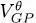 , defined as a one-particle operator whose matrix elements in an arbitrary basis are {| u i〉} given by:
, defined as a one-particle operator whose matrix elements in an arbitrary basis are {| u i〉} given by:
(40) 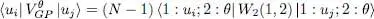
which leads to:
(41) 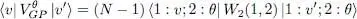
Читать дальше

 , we use a basis {| θ k〉} of the individual state space, whose first vector is | θ 1〉 = | θ 〉.
, we use a basis {| θ k〉} of the individual state space, whose first vector is | θ 1〉 = | θ 〉.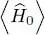 as:
as: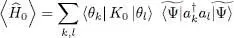
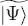 is a Fock state whose only non-zero population is that of the state | θ 1〉, the ket
is a Fock state whose only non-zero population is that of the state | θ 1〉, the ket  is non-zero only if l = 1; it is then orthogonal to
is non-zero only if l = 1; it is then orthogonal to 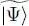 if k ≠ 1. Consequently, the only term left in the summation corresponds to k = l = 1. As the operator
if k ≠ 1. Consequently, the only term left in the summation corresponds to k = l = 1. As the operator 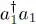 multiplies the ket by its population N , we get:
multiplies the ket by its population N , we get: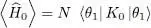
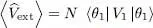
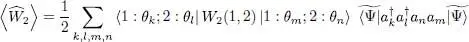
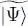 ). When all the subscripts are equal to 1, the operator multiplies the ket
). When all the subscripts are equal to 1, the operator multiplies the ket 
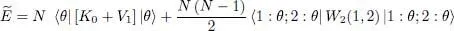
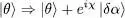
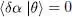
 of the variational energy, we get the sum of two terms: the first one comes from the variation of the ket | θ 〉 and is proportional to eiχ the second one comes from the variation of the bra 〈 θ | and is proportional to e–χ . The result has the form:
of the variational energy, we get the sum of two terms: the first one comes from the variation of the ket | θ 〉 and is proportional to eiχ the second one comes from the variation of the bra 〈 θ | and is proportional to e–χ . The result has the form: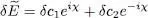
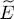 must hold for any arbitrary real value of χ . As before (§ 2-b- α ), it follows that both δc 1and δc 2are zero. Consequently, we can impose the variation
must hold for any arbitrary real value of χ . As before (§ 2-b- α ), it follows that both δc 1and δc 2are zero. Consequently, we can impose the variation 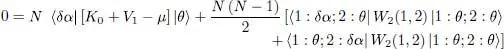
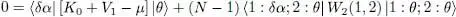
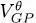 , defined as a one-particle operator whose matrix elements in an arbitrary basis are {| u i〉} given by:
, defined as a one-particle operator whose matrix elements in an arbitrary basis are {| u i〉} given by: