where | v 〉 and | v′ 〉 are two arbitrary one-particle kets – this can be shown by expanding these two kets on the basis {| u i〉} and using relation (40). Note that this potential operator does not include an exchange term; this term does not exist when the two interacting particles are in the same individual quantum state. Equation (39)then becomes:
(42) 
This stationarity condition must be verified for any value of the bra | δα 〉, with only the constraint that it must be orthogonal to | θ 〉 (according to relation (36)). This means that the ket resulting from the action of the operator  on | θ 〉 must have zero components on all the vectors orthogonal to | θ 〉; its only non-zero component must be on the ket | θ 〉 itself, which means it is necessarily proportional to | θ 〉. In other words, | θ 〉 must be an eigenvector of that operator, with eigenvalue μ (real since the operator is Hermitian):
on | θ 〉 must have zero components on all the vectors orthogonal to | θ 〉; its only non-zero component must be on the ket | θ 〉 itself, which means it is necessarily proportional to | θ 〉. In other words, | θ 〉 must be an eigenvector of that operator, with eigenvalue μ (real since the operator is Hermitian):
(43) 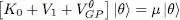
We have just shown that the optimal value | φ 〉 of | θ 〉 is the solution of the Gross-Pitaevskii equation:
(44) 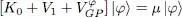
which is a generalization of (28)to particles with spin, and is valid for one- or two-body arbitrary potentials. For each particle, the operator 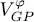 represents the mean field created by all the others in the same state | φ 〉.
represents the mean field created by all the others in the same state | φ 〉.
Comment:
The Gross-Pitaevskii operator 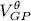 is simply a partial trace over the second particle:
is simply a partial trace over the second particle:
(45) 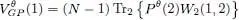
where Pθ (2) is the projection operator Pθ (2) of the state of particle 2 onto | θ 〉:
(46) 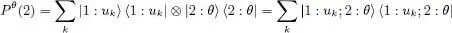
To show this, let us compute the partial trace on the right-hand side of (45). To obtain this trace (Complement E III, § 5-b), we choose for particle 2 a set of basis states {| θ n〉} whose first vector | θ 1〉 coincides with | θ 〉:
(47) 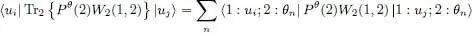
Replacing Pθ (2) by its value (46)yields the product of δik (for the scalar product associated with particle 1) and δ n1(for the one associated with particle 2). This leads to:
(48) 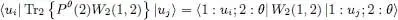
which is simply the initial definition (40)of 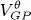 . Relation (45)is therefore another possible definition for the Gross-Pitaevskii potential.
. Relation (45)is therefore another possible definition for the Gross-Pitaevskii potential.
We have established which conditions the variational wave function must obey to make the energy stationary, but we have yet to study the actual value of this energy. This will allow us to show that the parameter μ is in fact the chemical potential associated with the system of interacting bosons. We shall then introduce the concept of a relaxation (or “healing”) length, and discuss the effect, on the final energy, of the fragmentation of a single condensate into several condensates, associated with distinct individual quantum states.
4-a. Energy and chemical potential
Since the ket | φ 〉 is normalized, multiplying (44)by the bra 〈 φ | and by N , we get:
(49) 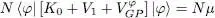
We recognize the first two terms of the left-hand side as the average values of the kinetic energy and the external potential. As for the last term, using definition (41)for 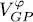 , we can write it as:
, we can write it as:
(50) 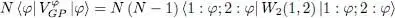
which is simply twice the potential interaction energy given in (33)when | θ 1〉 = | φ 〉. This leads to:
(51) 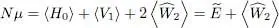
To find the energy 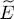 , note that N μ /2 is the sum of
, note that N μ /2 is the sum of 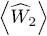 and of half the kinetic and external potential energies. Adding the missing halves, we finally get for
and of half the kinetic and external potential energies. Adding the missing halves, we finally get for 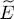 :
:
(52) 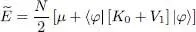
An advantage of this formula is to involve only one- (and not two-) particle operators, which simplifies the computations. The interaction energy is implicitly contained in the factor μ .
The quantity μ does not yield directly the average energy, but it is related to it, as we now show. Taking the derivative, with respect to N , of equation (34)written for | θ 〉 = | φ 〉, we get:
(53) 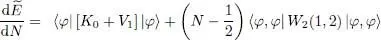
For large N , one can safely replace in this equation ( N — 1/2) by ( N — 1); after multiplication by N , we obtain a sum of average energies:
Читать дальше

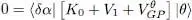
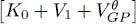 on | θ 〉 must have zero components on all the vectors orthogonal to | θ 〉; its only non-zero component must be on the ket | θ 〉 itself, which means it is necessarily proportional to | θ 〉. In other words, | θ 〉 must be an eigenvector of that operator, with eigenvalue μ (real since the operator is Hermitian):
on | θ 〉 must have zero components on all the vectors orthogonal to | θ 〉; its only non-zero component must be on the ket | θ 〉 itself, which means it is necessarily proportional to | θ 〉. In other words, | θ 〉 must be an eigenvector of that operator, with eigenvalue μ (real since the operator is Hermitian):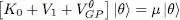
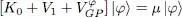
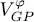 represents the mean field created by all the others in the same state | φ 〉.
represents the mean field created by all the others in the same state | φ 〉.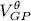 is simply a partial trace over the second particle:
is simply a partial trace over the second particle: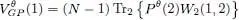
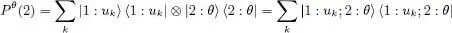
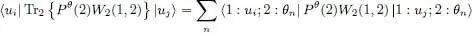
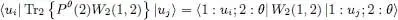
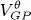 . Relation (45)is therefore another possible definition for the Gross-Pitaevskii potential.
. Relation (45)is therefore another possible definition for the Gross-Pitaevskii potential.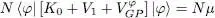
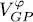 , we can write it as:
, we can write it as: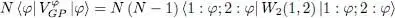
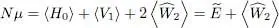
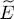 , note that N μ /2 is the sum of
, note that N μ /2 is the sum of 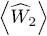 and of half the kinetic and external potential energies. Adding the missing halves, we finally get for
and of half the kinetic and external potential energies. Adding the missing halves, we finally get for