Instead of talking about particles and holes, one can also use a general term, excitations (or “quasi-particles”). The creation operator of an excitation of |k i| ≤ kF is the creation operator 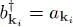 of a hole ; the creation operator of an excitation of |k i| > kF is the creation operator
of a hole ; the creation operator of an excitation of |k i| > kF is the creation operator 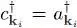 of a particle. The vacuum state defined initially is a common eigenvector of all the particle annihilation operators, with eigenvalues zero; in a similar way, the new vacuum state
of a particle. The vacuum state defined initially is a common eigenvector of all the particle annihilation operators, with eigenvalues zero; in a similar way, the new vacuum state 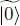 is a common eigenvector of all the excitation annihilation operators. We therefore call it the “quasi-particle vacuum”.
is a common eigenvector of all the excitation annihilation operators. We therefore call it the “quasi-particle vacuum”.
As we have neglected all particle interactions, the system Hamiltonian is written as:
(9) 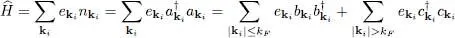
Taking into account the anticommutation relations between the operators b kiand  . we can rewrite this expression as:
. we can rewrite this expression as:
(10) 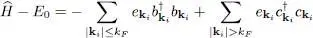
where E 0has been defined in (3)and simply shifts the origin of all the system energies. Relation (10)shows that holes (excitations with |k i| ≤ kF ) have a negative energy, as expected since they correspond to missing particles. Starting from its ground state, to increase the system energy keeping the particle number constant, we must apply the operator 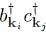 that creates both a particle and a hole: the system energy is then increased by the quantity ej — ei ; inversely, to decrease the system energy, the adjoint operator c kj b kimust be applied.
that creates both a particle and a hole: the system energy is then increased by the quantity ej — ei ; inversely, to decrease the system energy, the adjoint operator c kj b kimust be applied.
Comments:
(i) We have discussed the notion of hole in the context of free particles, but nothing in the previous discussion requires the one-particle energy spectrum to be simply quadratic as in (4). In semi-conductor physics for example, particles often move in a periodic potential, and occupy states in the “valence band” when their energy is lower than the Fermi level EF whereas the others occupy the “conduction band”, separated from the previous band by an “energy gap”. Sending a photon with an energy larger than this gap allows the creation of an electron-hole pair, easily studied in the formalism we just introduced.
A somewhat similar case occurs when studying the relativistic Dirac wave equation, where two energy continuums appear: one with energies greater than the electron rest energy mc 2(where m is the electron mass, and c the speed of light), and one for negative energies less than — mc 2associated with the positron (the antiparticle of the electron, having the opposite charge). The energy spectrum is relativistic, and thus different from formula (4), even inside each of those two continuums. However, the general formalism remains valid, the operators 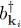 and b kidescribing now, respectively, the creation and annihilation of a positron. The Dirac equation however leads to difficulties by introducing for example an infinity of negative energy states, assumed to be all occupied to avoid problems. A proper treatment of this type of relativistic problems must be done in the framework of quantum field theory.
and b kidescribing now, respectively, the creation and annihilation of a positron. The Dirac equation however leads to difficulties by introducing for example an infinity of negative energy states, assumed to be all occupied to avoid problems. A proper treatment of this type of relativistic problems must be done in the framework of quantum field theory.
(ii) An arbitrary N -particle Fock state |Φ〉 does not have to be the ground state to be formally considered as a “quasi-particle vacuum”. We just have to consider any annihilation operator on an already occupied individual state as a creation operator of a hole (i.e. of an excitation); we then define the corresponding hole (or excitation) annihilation operators, which all have in common the eigenvector |Φ〉 with eigenvalue zero. This comment will be useful when studying the Wick theorem (Complement C XVI). In § E of Chapter XVII, we shall see another example of a quasi-particle vacuum, but where, this time, the new annihilation operators are no longer acting on individual states but on states of pairs of particles.
1 1 In Complement CXIV we had assumed that both spin states of the electron gas were occupied, whereas this is not the case here. This explains why the bracket in formula (1)contains the coefficient 6π2N instead of 3π2N.
Complement B XVIdeal gas in thermal equilibrium; quantum distribution functions
1 1 Grand canonical description of a system without interactions 1-a Density operator 1-b Grand canonical partition function, grand potential
2 2 Average values of symmetric one-particle operators 2-a Fermion distribution function 2-b Boson distribution function 2-c Common expression 2-d Characteristics of Fermi-Dirac and Bose-Einstein distributions
3 3 Two-particle operators 3-a Fermions 3-b Bosons 3-c Common expression
4 4 Total number of particles 4-a Fermions 4-b Bosons
5 5 Equation of state, pressure 5-a Fermions 5-b Bosons
This complement studies the average values of one- or two-particle operators for an ideal gas, in thermal equilibrium. It includes a discussion of several useful properties of the Fermi-Dirac and Bose-Einstein distribution functions, already introduced in Chapter XIV.
To describe thermal equilibrium, statistical mechanics often uses the grand canonical ensemble, where the particle number may fluctuate, with an average value fixed by the chemical potential μ (cf. Appendix VI, where you will find a number of useful concepts for reading this complement). This potential plays, with respect to the particle number, a role similar to the role the inverse of the temperature term β = 1/ kBT plays with respect to the energy ( kB is the Boltzmann constant). In quantum statistical mechanics, Fock space is a good choice for the grand canonical ensemble as it easily allows changing the total number of particles. As a direct application of the results of §§ B and C of Chapter XV, we shall compute the average values of symmetric one- or two-particle operators for a system of identical particles in thermal equilibrium.
We begin in § 1 with the density operator for non-interacting particles, and then show in §§ 2 and 3 that the average values of the symmetric operators may be expressed in terms of the Fermi-Dirac and Bose-Einstein distribution functions, increasing their application range and hence their importance. In § 5, we shall study the equation of state for an ideal gas of fermions or bosons at temperature T and contained in a volume 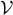 .
.
1. Grand canonical description of a system without interactions
We first recall how a system of non-interacting particles is described, in quantum statistical mechanics, by the grand canonical ensemble; more details on this subject can be found in Appendix VI, § 1-c.
Читать дальше

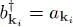 of a hole ; the creation operator of an excitation of |k i| > kF is the creation operator
of a hole ; the creation operator of an excitation of |k i| > kF is the creation operator 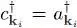 of a particle. The vacuum state defined initially is a common eigenvector of all the particle annihilation operators, with eigenvalues zero; in a similar way, the new vacuum state
of a particle. The vacuum state defined initially is a common eigenvector of all the particle annihilation operators, with eigenvalues zero; in a similar way, the new vacuum state 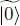 is a common eigenvector of all the excitation annihilation operators. We therefore call it the “quasi-particle vacuum”.
is a common eigenvector of all the excitation annihilation operators. We therefore call it the “quasi-particle vacuum”.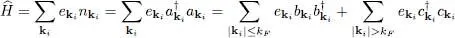
 . we can rewrite this expression as:
. we can rewrite this expression as: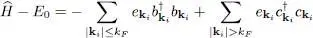
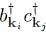 that creates both a particle and a hole: the system energy is then increased by the quantity ej — ei ; inversely, to decrease the system energy, the adjoint operator c kj b kimust be applied.
that creates both a particle and a hole: the system energy is then increased by the quantity ej — ei ; inversely, to decrease the system energy, the adjoint operator c kj b kimust be applied.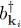 and b kidescribing now, respectively, the creation and annihilation of a positron. The Dirac equation however leads to difficulties by introducing for example an infinity of negative energy states, assumed to be all occupied to avoid problems. A proper treatment of this type of relativistic problems must be done in the framework of quantum field theory.
and b kidescribing now, respectively, the creation and annihilation of a positron. The Dirac equation however leads to difficulties by introducing for example an infinity of negative energy states, assumed to be all occupied to avoid problems. A proper treatment of this type of relativistic problems must be done in the framework of quantum field theory. .
.










