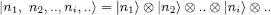(A-6) 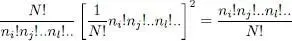
We shall therefore choose for c the inverse of the square root of that number, leading to the normalized ket:
(A-7) 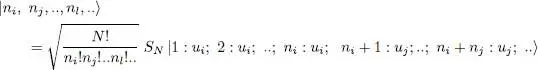
These states are called the “ Fock states ”, for which the occupation numbers are well defined.
For the Fock states, it is sometimes handy to use a slightly different but equivalent notation. In (A-7), these states are defined by specifying the occupation numbers of all the states that are actually occupied ( ni ≥ 1). Another option would be to indicate all the occupation numbers including those which are zero 3 – this is what we have explicitly done in (A-4). We then write the same kets as:
(A-8) 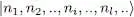
Another possibility is to specify a list of N occupied states, where ui is repeated ni times, uj repeated nj times, etc. :
(A-9) 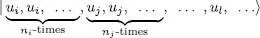
As we shall see later, this latter notation is sometimes useful in computations involving both bosons and fermions.
A-1-b. Fock states for identical fermions
In the case of fermions, the operator AN acting on a ket where two (or more) numbered particles are in the same individual state yields a zero result: there are no such states in the physical space A ( N ). Hence we concentrate on the case where all the occupation numbers are either 1 or 0. We denote | ui 〉, | uj 〉,..,| ul 〉,.. all the states having an occupation number equal to 1. The equivalent for fermions of formula (A-7)is written:
(A-10) 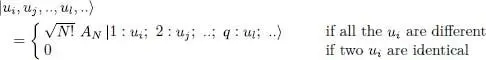
Taking into account the 1/ N factor appearing in definition (A-3)of AN the right-hand side of this equation is a linear superposition, with coefficients 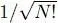 , of N ! kets which are all orthogonal to each other (as we have chosen an orthonormal basis for the individual states {| uk 〉}); hence its norm is equal to 1. Consequently, Fock states for fermions are defined by (A-10). Contrary to bosons, the main concern is no longer how many particles occupy a state, but whether a state is occupied or not. Another difference with the boson case is that, for fermions, the order of the states matters. If for instance the first two states ui and uj are exchanged, we get the opposite ket:
, of N ! kets which are all orthogonal to each other (as we have chosen an orthonormal basis for the individual states {| uk 〉}); hence its norm is equal to 1. Consequently, Fock states for fermions are defined by (A-10). Contrary to bosons, the main concern is no longer how many particles occupy a state, but whether a state is occupied or not. Another difference with the boson case is that, for fermions, the order of the states matters. If for instance the first two states ui and uj are exchanged, we get the opposite ket:
(A-11) 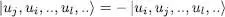
but it obviously does not change the physical meaning of the ket.
The Fock states are the building blocks used to construct this whole chapter. We have until now considered separately the spaces S, A ( N ) associated with different values of the particle number N . We shall now regroup them into a single space, called the “ Fock space ”, using the direct sum 4formalism. For bosons:
(A-12) 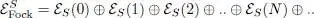
and, for fermions:
(A-13) 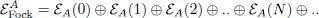
(the sums go to infinity). In both cases, we have included on the right-hand side a first term associated with a total number of particles equal to zero. The corresponding space, S,A (0), is defined as a one-dimensional space, containing a single state called “vacuum” and denoted |0〉 or |vac〉. For bosons as well as fermions, an orthonormal basis for the Fock space can be built with the Fock states | n 1, n 2, …, ni , nl ..〉, relaxing the constraint (A-4): the occupation numbers may then take on any (integer) values, including zeros for all, which corresponds to the vacuum ket |0〉. Linear combinations of all these basis vectors yield all the vectors of the Fock space, including linear superpositions of kets containing different particle numbers. It is not essential to attribute a physical interpretation to such superpositions since they can be considered as intermediate states of the calculation. Obviously, the Fock space contains many kets with well defined particle numbers: all those belonging to a single sub-space S ( N ) for bosons, or A ( N ) for fermions. Two kets having different particle numbers N are necessarily orthogonal; for example, all the kets having a non-zero total population are orthogonal to the vacuum state.
Comments:
(i) Contrary to the distinguishable particle case, the Fock space is not the tensor product of the spaces of states associated with particles numbered 1, 2,…, q , etc. First of all, for a fixed N , it only includes the totally symmetric (or antisymmetric) subspace of this tensor product; furthermore, the Fock space is the direct sum of such subspaces associated with each value of the particle number N .
The Fock space is, however, the tensor product of Fock spaces 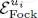 associated with the individual orthogonal states | ui 〉, each
associated with the individual orthogonal states | ui 〉, each 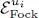 being spanned by the kets | ni 〉 where ni takes on all integer values (from zero to infinity for bosons, from zero to one for fermions):
being spanned by the kets | ni 〉 where ni takes on all integer values (from zero to infinity for bosons, from zero to one for fermions):
(A-14) 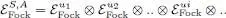
This is because the Fock states, which are a basis for 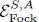 , may be written as the tensor product:
, may be written as the tensor product:
(A-15) 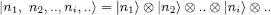
It is often said that each individual state defines a “mode” of the system of identical particles. Decomposing the Fock state into a tensor product allows considering the modes as describing different and distinguishable variables. This will be useful on numerous occasions (see for example Complements B XV, D XVand E XV).
Читать дальше

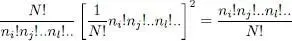
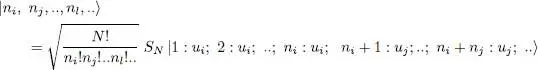
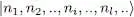
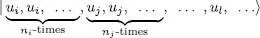
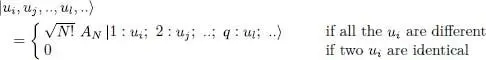
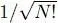 , of N ! kets which are all orthogonal to each other (as we have chosen an orthonormal basis for the individual states {| uk 〉}); hence its norm is equal to 1. Consequently, Fock states for fermions are defined by (A-10). Contrary to bosons, the main concern is no longer how many particles occupy a state, but whether a state is occupied or not. Another difference with the boson case is that, for fermions, the order of the states matters. If for instance the first two states ui and uj are exchanged, we get the opposite ket:
, of N ! kets which are all orthogonal to each other (as we have chosen an orthonormal basis for the individual states {| uk 〉}); hence its norm is equal to 1. Consequently, Fock states for fermions are defined by (A-10). Contrary to bosons, the main concern is no longer how many particles occupy a state, but whether a state is occupied or not. Another difference with the boson case is that, for fermions, the order of the states matters. If for instance the first two states ui and uj are exchanged, we get the opposite ket: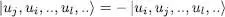
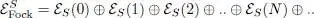
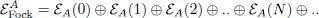
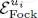 associated with the individual orthogonal states | ui 〉, each
associated with the individual orthogonal states | ui 〉, each 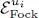 being spanned by the kets | ni 〉 where ni takes on all integer values (from zero to infinity for bosons, from zero to one for fermions):
being spanned by the kets | ni 〉 where ni takes on all integer values (from zero to infinity for bosons, from zero to one for fermions):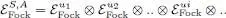
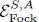 , may be written as the tensor product:
, may be written as the tensor product: