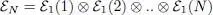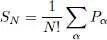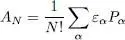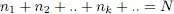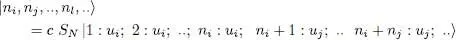Claude Cohen-Tannoudji - Quantum Mechanics, Volume 3

Pierre-François Cohadon

Jean Dalibard

Sébastien Gleyzes

Markus Holzmann

Thibaut Jacqmin

Philippe Jacquier

Amaury Mouchet

Jean-Michel Raimond

Félix Werner

Some delicate aspects of Latex typography have been resolved thanks to Marco Picco, Pierre Cladé and Jean Hare. Roger Balian, Edouard Brézin and William Mullin have offered useful advice and suggestions. Finally, our sincere thanks go to Geneviève Tastevin, Pierre-François Cohadon and Samuel Deléglise for their help with a number of figures.

1 A General formalism A-1 Fock states and Fock space A-2 Creation operators a † A-3 Annihilation operators a A-4 Occupation number operators (bosons and fermions) A-5 Commutation and anticommutation relations A-6 Change of basis

2 B One-particle symmetric operators B-1 Definition B-2 Expression in terms of the operators a and a † B-3 Examples B-4 Single particle density operator

3 C Two-particle operators C-1 Definition C-2 A simple case: factorization C-3 General case C-4 Two-particle reduced density operator C-5 Physical discussion; consequences of the exchange

For a system composed of identical particles, the particle numbering used in Chapter XIV, the last chapter of Volume II [2], does not really have much physical significance. Furthermore, when the particle number gets larger than a few units, applying the symmetrization postulate to numbered particles often leads to complex calculations. For example, computing the average value of a symmetric operator requires the symmetrization of the bra, the ket, and finally the operator, which introduces a large number of terms 1 . They seem different, a priori, but at the end of the computation many are found to be equal, or sometimes cancel each other. Fortunately, these lengthy calculations may be avoided using an equivalent method based on creation and annihilation operators in a “Fock space”. The simple commutation (or anticommutation) rules satisfied by these operators are the expression of the symmetrization (or antisymmetrization) postulate. The non-physical particle numbering is replaced by assigning “occupation numbers” to individual states, which is more natural for treating identical particles.

The method described in this chapter and the following is sometimes called “second quantization” 2 . It deals with operators that no longer conserve the particle number, hence acting in a state space larger than those we have previously considered; this new space is called the “Fock space” (§ A). These operators which change the particle number appear mainly in the course of calculations, and often regroup at the end, keeping the total particle number constant. Examples will be given (§ B) for one-particle symmetric operators, such as the total linear momentum or angular momentum of a system of identical particles. We shall then study two-particle symmetric operators (§ C), such as the energy of a system of interacting identical particles, their spatial correlation function, etc. In quantum statistical mechanics, the Fock space is well adapted to computations performed in the “grand canonical” ensemble, where the total number of particles may fluctuate since the system is in contact with an external reservoir. Furthermore, as we shall see in the following chapters, the Fock space is very useful for describing physical processes where the particle number changes, as in photon absorption or emission.

We denote N the state space of a system of N distinguishable particles, which is the tensor product of N individual state spaces 1:

(A-1)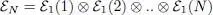

Two sub-spaces of N are particularly important for identical particles, as they contain all their accessible physical states: the space S ( N ) of the completely symmetric states for bosons, and the space A ( N ) of the completely antisymmetric states for fermions. The projectors onto these two sub-spaces are given by relations (B-49) and (B-50) of Chapter XIV:

(A-2)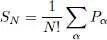

and:

(A-3)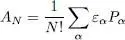

where the Pα are the N ! permutation operators for the N particles, and εα the parity of Pα (in this chapter we have added for clarity the index N to the projectors S and A defined in Chapter XIV).

Starting from an arbitrary orthonormal basis {| uk 〉} of the state space for one particle, we constructed in § C-3-d of Chapter XIV a basis of the state space for N identical particles. Its vectors are characterized by the occupation numbers ni , with:

(A-4)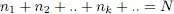

where n 1is the occupation number of the first basis vector | u 1〉 (i.e. the number of particles in | u 1〉), n 2that of | u 2〉, .., nk that of | uk 〉. In this series of numbers, some (even many) may be zero: a given state has no particular reason to always be occupied. It is therefore often easier to specify only the non-zero occupation numbers, which will be noted ni , nj , .., ni ,.. . This series indicates that the first basis state that has at least one particle is | ui 〉 and it contains ni particles; the second occupied state is | uj 〉 with a population nj , etc. As in (A-4), these occupation numbers add up to N .

Comment:

In this chapter we constantly use subscripts of different types, which should not be confused. The subscripts i , j , k , l , ..denote different basis vectors {| ui 〉} of the state space 1of a single particle; they span values given by the dimension of this state space, which often goes to infinity. They should not be confused with the subscripts used to number the particles, which can take N different values, and are labeled q , q ′, etc. Finally the subscript α distinguishes the different permutations of the N particles, and can therefore take N ! different values.

For bosons, the basis vectors can be written as in (C-15)of Chapter XIV:

(A-5)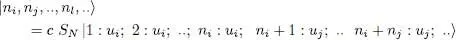

where c is a normalization constant; on the right-hand side, ni particles occupy the state | ui 〉, nj the state | uj 〉, etc… (because of symmetrization, their order does not matter).

Let us calculate the norm of the right-hand term. It is composed of N ! terms, coming from each of the N ! permutations included in SN , but only some of them are orthogonal to each other: all the permutations Pα leading to redistributions of the nj first particles among themselves, of the next nj particles among themselves, etc. yield the same initial ket. On the other hand, if a permutation changes the individual state of one (or more than one) particle, it yields a different ket, actually orthogonal to the initial ket. This means that the different permutations contained in SN can be grouped into families of ni ! nj !.. nl !.. equivalent permutations, all yielding the same ket; taking into account the factor N ! appearing in the definition of SN , the coefficient in front of this ket becomes ni ! nj !.. nl !../ N ! and its contribution to the norm of the ket is equal to the square of this number. On the other hand, the number of orthogonal kets is N !/ ni ! nj !.. nl !.. Consequently if c was equal to 1 in formula (A-5), the ket thus defined would have a norm equal to: