Its diagonal matrix elements are then written:
(90) 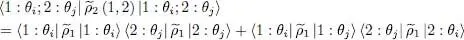
and are the sum of a direct term, and an exchange term. When i ≠ j , the presence of an exchange term is not surprising, and corresponds to the general discussion of § C-5 in Chapter XV. It is similar to the expression of the spatial correlation function written in (C-34) of that chapter, which is also the sum of two contributions, a direct one (C-32) and an exchange one (C-33). Since this last contribution is positive when r 1≃ r 2, the physical consequence of the exchange is a spatial bunching of the bosons. What is surprising though is that the exchange term still exists in (90)when i = j , even though the notion of exchange is meaningless: when dealing with a single individual state, the four expressions (C-21) of Chapter XVreduce to a single one, the direct term. We can also check that the exchange term (C-34) of Chapter XVincludes the explicit condition i ≠ j , which means it receives no contribution from i = j . We shall furthermore confirm in § 3 of Complement A XVIthat bosons all placed in the same individual quantum state are not spatially correlated, and therefore present neither bunching nor exchange effects. The mathematical expression of the trial two-particle Hartree-Fock density operator thus contains too many exchange terms. This does not really matter as long as the boson system remains far from Bose-Einstein condensation: the error involved is small since the x = j terms play a negligible role compared to the i ≠ j terms in the summations over i and j appearing in the interaction energy. However, as soon as an individual state becomes highly populated, significant errors can occur and the Hartree-Fock method must be abandoned. There exist, however, more elaborate theoretical treatments better adapted to this case.
3-c. Differences with the zero-temperature Hartree-Fock equations (fermions)
The main difference between the approach we just used and that of Complements C XVand E XVis that these complements were only looking for a single eigenstate of the Hamiltonian Ĥ , generally its ground state. If we are now interested in several of these states, we have to redo the computation separately for each of them. To study the properties of thermal equilibrium, one could imagine doing the calculations a great many times, and then weigh the results with occupation probabilities. This method obviously leads to heavy computations, which become impossible for a macroscopic system having an extremely large number of levels. In the present complement, the Hartree-Fock equations yield immediately thermal averages, as well as eigenvectors of a one-particle density operator with their energies.
Another important difference is that the Hartree-Fock operator now depends on the temperature, because of the presence in (85)of a temperature dependent distribution function – or, which amounts to the same thing, of the presence in (84)of an operator dependent on β , and which replaces the projector PN (2)onto all the populated individual states. The equations obtained remind us of those governing independent particles, each finding its thermodynamic equilibrium while moving in the self-consistent mean field created by all the others, also including the exchange contribution (which can be ignored in the simplified “Hartree” version).
We must keep in mind, however, that the Hartree-Fock potential associated with each individual state now depends on the populations of an infinity of other individual states, and these populations are function of their energy as well as of the temperature. In other words, because of the nonlinear character of the Hartree-Fock equations, the computation is not merely a juxtaposition of separate mean field calculations for stationary individual states.
3-d. Zero-temperature limit (fermions)
Let us check that the Hartree-Fock method for non-zero temperature yields the same results as the zero temperature method explained in Complement E XVfor fermions.
In § 2-d of Complement B XV, we introduced for an ideal gas the concept of a degenerate quantum gas. It can be generalized to a gas with interactions: in a fermion system, when βμ ≫ 1, the system is said to be strongly degenerate. As the temperature goes to zero, a fermion system becomes more and more degenerate. Can we be certain that the results of this complement are in agreement with those of Complement E XV, valid at zero temperature?
We saw that the temperature comes into play in the definition (85)of the mean Hartree-Fock potential, WHF . In the limit of a very strong degeneracy, the Fermi-Dirac distribution function appearing in the definition (40)of 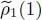 becomes practically a step function, equal to 1 for energies ej less than the chemical potential μ , and zero otherwise ( Figure 1of Complement B XV. In other words, the only populated states (and by a single fermion) are the states having energies less than μ , i.e. less than the Fermi level. Under such conditions, the
becomes practically a step function, equal to 1 for energies ej less than the chemical potential μ , and zero otherwise ( Figure 1of Complement B XV. In other words, the only populated states (and by a single fermion) are the states having energies less than μ , i.e. less than the Fermi level. Under such conditions, the 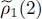 of (84)becomes practically equal to the projector PN (2) which, in Complement E XV, appears in the definition (52)of the zero-temperature Hartree-Fock potential; in other words, the partial trace appearing in this relation (85)is then strictly limited to the individual states having the lowest energies. We thus obtain the same Hartree Fock equations as for zero temperature, leading to the determination of a set of individual eigenstates on which we can build a unique N -particle state.
of (84)becomes practically equal to the projector PN (2) which, in Complement E XV, appears in the definition (52)of the zero-temperature Hartree-Fock potential; in other words, the partial trace appearing in this relation (85)is then strictly limited to the individual states having the lowest energies. We thus obtain the same Hartree Fock equations as for zero temperature, leading to the determination of a set of individual eigenstates on which we can build a unique N -particle state.
3-e. Wave function equations
Let us write the Hartree-Fock equations (87)in terms of wave functions: these equations are strictly equivalent to (87), written in terms of operators and kets, but their form is sometimes easier to use, in particular for numerical calculations.
Assuming the particles have a spin, we shall note the wave functions φν ( r), with:
(91) 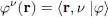
where the spin quantum number ν can take (2 S + 1) values; according to the nature of the particles, the possible spins S are S = 0, S = 1/2, S = 1 etc. As in Complement E XV(§ 2-d), we introduce a complete basis 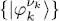 for the individual state space, built from kets that are all eigenvectors of the spin component along the quantization axis, with eigenvalue νk . For each value of n , the spin index ν takes on a given value νn and is not, therefore, an independent index. As for the potentials, we assume here again that V 1is diagonal in ν , but that its diagonal elements
for the individual state space, built from kets that are all eigenvectors of the spin component along the quantization axis, with eigenvalue νk . For each value of n , the spin index ν takes on a given value νn and is not, therefore, an independent index. As for the potentials, we assume here again that V 1is diagonal in ν , but that its diagonal elements 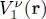 may depend on ν . The interaction potential, however, is described by a function W 2( r, r′) that only depends on r– r′, but does not act on the spins.
may depend on ν . The interaction potential, however, is described by a function W 2( r, r′) that only depends on r– r′, but does not act on the spins.
Читать дальше

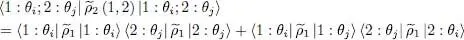
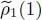 becomes practically a step function, equal to 1 for energies ej less than the chemical potential μ , and zero otherwise ( Figure 1of Complement B XV. In other words, the only populated states (and by a single fermion) are the states having energies less than μ , i.e. less than the Fermi level. Under such conditions, the
becomes practically a step function, equal to 1 for energies ej less than the chemical potential μ , and zero otherwise ( Figure 1of Complement B XV. In other words, the only populated states (and by a single fermion) are the states having energies less than μ , i.e. less than the Fermi level. Under such conditions, the 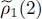 of (84)becomes practically equal to the projector PN (2) which, in Complement E XV, appears in the definition (52)of the zero-temperature Hartree-Fock potential; in other words, the partial trace appearing in this relation (85)is then strictly limited to the individual states having the lowest energies. We thus obtain the same Hartree Fock equations as for zero temperature, leading to the determination of a set of individual eigenstates on which we can build a unique N -particle state.
of (84)becomes practically equal to the projector PN (2) which, in Complement E XV, appears in the definition (52)of the zero-temperature Hartree-Fock potential; in other words, the partial trace appearing in this relation (85)is then strictly limited to the individual states having the lowest energies. We thus obtain the same Hartree Fock equations as for zero temperature, leading to the determination of a set of individual eigenstates on which we can build a unique N -particle state.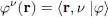
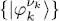 for the individual state space, built from kets that are all eigenvectors of the spin component along the quantization axis, with eigenvalue νk . For each value of n , the spin index ν takes on a given value νn and is not, therefore, an independent index. As for the potentials, we assume here again that V 1is diagonal in ν , but that its diagonal elements
for the individual state space, built from kets that are all eigenvectors of the spin component along the quantization axis, with eigenvalue νk . For each value of n , the spin index ν takes on a given value νn and is not, therefore, an independent index. As for the potentials, we assume here again that V 1is diagonal in ν , but that its diagonal elements 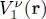 may depend on ν . The interaction potential, however, is described by a function W 2( r, r′) that only depends on r– r′, but does not act on the spins.
may depend on ν . The interaction potential, however, is described by a function W 2( r, r′) that only depends on r– r′, but does not act on the spins.










