(66) 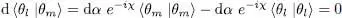
The variations (65)are therefore acceptable, for any real value of χ .
We now compute how they change the operator 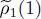 defined in (40). In the sum over k , only the k = l and k = m terms will change. The k = l term yields a variation:
defined in (40). In the sum over k , only the k = l and k = m terms will change. The k = l term yields a variation:
(67) 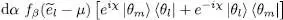
whereas the k = m term yields a similar variation but where 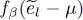 is replaced by
is replaced by 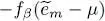 . This leads to:
. This leads to:
(68) 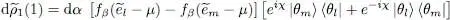
We now include these variations in the three terms of (61); as the distributions f are unchanged, only the terms 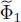 and
and 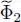 will vary. The infinitesimal variation of
will vary. The infinitesimal variation of 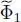 is written as:
is written as:
(69) 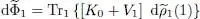
As for 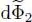 , it contains two contributions, one from
, it contains two contributions, one from 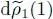 and one from
and one from 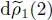 . These two contributions are equal since the operator W 2(1,2) is symmetric (particles 1 and 2 play an equivalent role). The factor 1/2 in
. These two contributions are equal since the operator W 2(1,2) is symmetric (particles 1 and 2 play an equivalent role). The factor 1/2 in 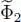 disappears and we get:
disappears and we get:
(70) 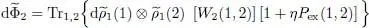
We can regroup these two contributions, using the fact that for any operator O (12), it can be shown that:
(71) 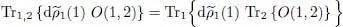
This equality is simply demonstrated 5 by using the definition of the partial trace Tr 2{ O (1,2)} of operator O (1, 2) with respect to particle 2. We then get:
(72) 
Inserting now the expression (68)for  , we get two terms, one proportional to eiχ , another one to e–iχ , whose value is:
, we get two terms, one proportional to eiχ , another one to e–iχ , whose value is:
(73) 
Now, for any operator O (1), we can write:
(74) 
so that the variation (73)can be expressed as:
(75) 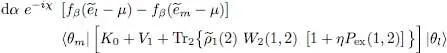
The term in eiχ has a similar form, but it does not have to be computed for the following reason. The variation 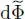 is the sum of a term in eiχ and another in e–iχ :
is the sum of a term in eiχ and another in e–iχ :
(76) 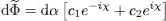
and the stationarity condition requires 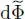 to be zero for any choice of Choosing χ = 0, yields c 1+ c 2= 0; choosing χ = π/2, and multiplying by – i , we get c 1– c 2= 0. Adding and subtracting those two relations shows that both coefficients c 1and c 2must be zero. Consequently, it suffices to impose the terms in e±iχ , and hence expression (75), to be zero. When
to be zero for any choice of Choosing χ = 0, yields c 1+ c 2= 0; choosing χ = π/2, and multiplying by – i , we get c 1– c 2= 0. Adding and subtracting those two relations shows that both coefficients c 1and c 2must be zero. Consequently, it suffices to impose the terms in e±iχ , and hence expression (75), to be zero. When 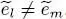 , the distribution functions fβ are not equal, and we get:
, the distribution functions fβ are not equal, and we get:
(77) 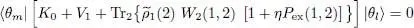
(if 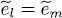 , however, we have not yet obtained any particular condition to be satisfied 6 ).
, however, we have not yet obtained any particular condition to be satisfied 6 ).
β. Variation of the energies
Let us now see what happens if the energy 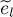 varies by
varies by 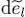 . The function
. The function 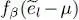 then varies by
then varies by 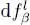 which, according to relation (40), induces a variation of
which, according to relation (40), induces a variation of 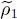 :
:
Читать дальше

 defined in (40). In the sum over k , only the k = l and k = m terms will change. The k = l term yields a variation:
defined in (40). In the sum over k , only the k = l and k = m terms will change. The k = l term yields a variation:
 is replaced by
is replaced by 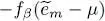 . This leads to:
. This leads to: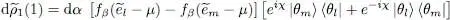
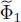 and
and 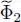 will vary. The infinitesimal variation of
will vary. The infinitesimal variation of 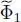 is written as:
is written as: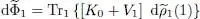
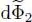 , it contains two contributions, one from
, it contains two contributions, one from 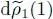 and one from
and one from 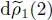 . These two contributions are equal since the operator W 2(1,2) is symmetric (particles 1 and 2 play an equivalent role). The factor 1/2 in
. These two contributions are equal since the operator W 2(1,2) is symmetric (particles 1 and 2 play an equivalent role). The factor 1/2 in 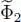 disappears and we get:
disappears and we get: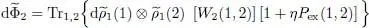
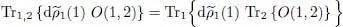
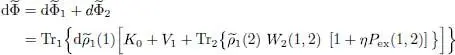
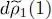 , we get two terms, one proportional to eiχ , another one to e–iχ , whose value is:
, we get two terms, one proportional to eiχ , another one to e–iχ , whose value is: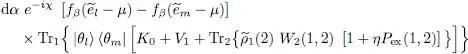
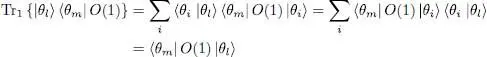
 is the sum of a term in eiχ and another in e–iχ :
is the sum of a term in eiχ and another in e–iχ :
 , the distribution functions fβ are not equal, and we get:
, the distribution functions fβ are not equal, and we get: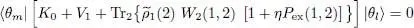
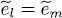 , however, we have not yet obtained any particular condition to be satisfied 6 ).
, however, we have not yet obtained any particular condition to be satisfied 6 ).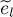 varies by
varies by 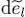 . The function
. The function 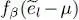 then varies by
then varies by 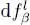 which, according to relation (40), induces a variation of
which, according to relation (40), induces a variation of 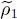 :
:










