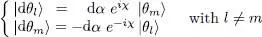The computation of the average value 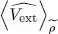 follows the same steps:
follows the same steps:
(57) 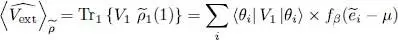
(as in Complement E XV, operator V 1is the one-particle external potential operator).
To complete the calculation of the average value of Ĥ , we now have to compute the trace 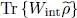 , the average value of the interaction energy when the system is described by
, the average value of the interaction energy when the system is described by 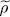 . Using relation (51)we can write this average value as a double trace:
. Using relation (51)we can write this average value as a double trace:
(58) 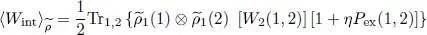
We now turn to the average value of 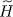 . The calculation is simplified since
. The calculation is simplified since 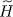 is, like Ĥ 0, a one-particle operator; furthermore, the | θi 〉 have been chosen to be the eigenvectors of
is, like Ĥ 0, a one-particle operator; furthermore, the | θi 〉 have been chosen to be the eigenvectors of 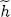 with eigenvalues
with eigenvalues 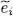 – see relation (26). We just replace in (56), Ĥ 0by
– see relation (26). We just replace in (56), Ĥ 0by 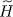 , and obtain:
, and obtain:
(59) 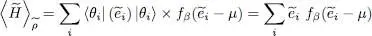
Regrouping all these results and using relation (36), we can write the variational grand potential as the sum of three terms:
(60) 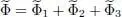
with:
(61) 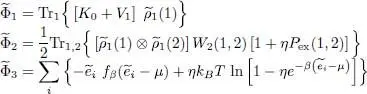
We now vary the eigenenergies 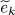 and eigenstates | θk 〉 of
and eigenstates | θk 〉 of 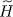 to find the value of the density operator
to find the value of the density operator 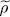 that minimizes the average value
that minimizes the average value 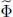 of the potential. We start with the variations of the eigenstates, which induce no variation of
of the potential. We start with the variations of the eigenstates, which induce no variation of 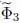 . The computation is actually very similar to that of Complement E XV, with the same steps: variation of the eigenvectors, followed by the demonstration that the stationarity condition is equivalent to a series of eigenvalue equations for a Hartree-Fock operator (a one-particle operator). Nevertheless, we will carry out this computation in detail, as there are some differences. In particular, and contrary to what happened in Complement E XV, the number of states | θi 〉 to be varied is no longer fixed by the particle number N ; these states form a complete basis of the individual state space, and their number can go to infinity. This means that we can no longer give to one (or several) state(s) a variation orthogonal to all the other | θj 〉; this variation will necessarily be a linear combination of these states. In a second step, we shall vary the energies
. The computation is actually very similar to that of Complement E XV, with the same steps: variation of the eigenvectors, followed by the demonstration that the stationarity condition is equivalent to a series of eigenvalue equations for a Hartree-Fock operator (a one-particle operator). Nevertheless, we will carry out this computation in detail, as there are some differences. In particular, and contrary to what happened in Complement E XV, the number of states | θi 〉 to be varied is no longer fixed by the particle number N ; these states form a complete basis of the individual state space, and their number can go to infinity. This means that we can no longer give to one (or several) state(s) a variation orthogonal to all the other | θj 〉; this variation will necessarily be a linear combination of these states. In a second step, we shall vary the energies 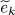 .
.
α. Variations of the eigenstates
As the eigenstates | θi 〉 vary, they must still obey the orthogonality relations:
(62) 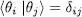
The simplest idea would be to vary only one of them, | θl 〉 for example, and make the change:
(63) 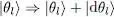
The orthogonality conditions would then require:
(64) 
preventing |d θl 〉 from having a component on any ket | θi 〉 other than | θl 〉: in other words, |d θl 〉 and | θl 〉 would be colinear. As | θl 〉 must remain normalized, the only possible variation would thus be a phase change, which does not affect either the density operator 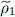 (1) or any average values computed with
(1) or any average values computed with 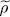 . This variation does not change anything and is therefore irrelevant.
. This variation does not change anything and is therefore irrelevant.
It is actually more interesting to vary simultaneously two eigenvectors, which will be called | θl 〉 and | θm 〉, as it is now possible to give | θl 〉 a component on | θm 〉, and the reverse. This does not change the two-dimensional subspace spanned by these two states; hence their orthogonality with all the other basis vectors is automatically preserved. Let us give the two vectors the following infinitesimal variations (without changing their energies 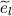 and
and 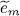 ):
):
(65) 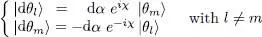
where da is an infinitesimal real number and χ an arbitrary but fixed real number. For any value of χ , we can check that the variation of 〈 θl | θl 〉 is indeed zero (it contains the scalar products 〈 θl | θm 〉 or 〈 θm | θl 〉 which are zero), as is the symmetrical variation of 〈 θm | θm 〉, and that we have:
Читать дальше

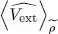 follows the same steps:
follows the same steps: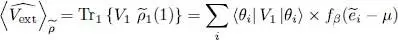
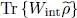 , the average value of the interaction energy when the system is described by
, the average value of the interaction energy when the system is described by 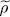 . Using relation (51)we can write this average value as a double trace:
. Using relation (51)we can write this average value as a double trace: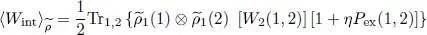
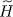 . The calculation is simplified since
. The calculation is simplified since 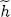 with eigenvalues
with eigenvalues 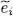 – see relation (26). We just replace in (56), Ĥ 0by
– see relation (26). We just replace in (56), Ĥ 0by 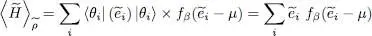
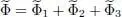
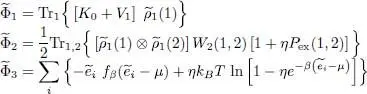
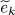 and eigenstates | θk 〉 of
and eigenstates | θk 〉 of 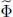 of the potential. We start with the variations of the eigenstates, which induce no variation of
of the potential. We start with the variations of the eigenstates, which induce no variation of 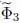 . The computation is actually very similar to that of Complement E XV, with the same steps: variation of the eigenvectors, followed by the demonstration that the stationarity condition is equivalent to a series of eigenvalue equations for a Hartree-Fock operator (a one-particle operator). Nevertheless, we will carry out this computation in detail, as there are some differences. In particular, and contrary to what happened in Complement E XV, the number of states | θi 〉 to be varied is no longer fixed by the particle number N ; these states form a complete basis of the individual state space, and their number can go to infinity. This means that we can no longer give to one (or several) state(s) a variation orthogonal to all the other | θj 〉; this variation will necessarily be a linear combination of these states. In a second step, we shall vary the energies
. The computation is actually very similar to that of Complement E XV, with the same steps: variation of the eigenvectors, followed by the demonstration that the stationarity condition is equivalent to a series of eigenvalue equations for a Hartree-Fock operator (a one-particle operator). Nevertheless, we will carry out this computation in detail, as there are some differences. In particular, and contrary to what happened in Complement E XV, the number of states | θi 〉 to be varied is no longer fixed by the particle number N ; these states form a complete basis of the individual state space, and their number can go to infinity. This means that we can no longer give to one (or several) state(s) a variation orthogonal to all the other | θj 〉; this variation will necessarily be a linear combination of these states. In a second step, we shall vary the energies 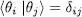
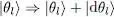

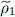 (1) or any average values computed with
(1) or any average values computed with 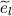 and
and 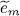 ):
):